高手支招！快速解决复杂的嵌入式人机界面开发

显示屏

智能化的今天，越来越多的产品更加注重用户体验了，很多电子产品上都会配备一款显示屏，以提高产品的档次，同时也方便人机交互。这里，复杂的人机界面设计在嵌入式开发中就成了一个痛点。

目前，大多数电子产品使用的显示屏，还是以LCD（液晶显示器）为主。

用LCD开发一款酷炫界面的产品，通常有两种方法：1.用现成GUI技术实现；2.基于LCM模组二次开发；两种方式各有各的特点。

LCD（液晶显示器）和LCM（液晶模组）的区别

LCD：Liquid Crystal Display，液晶显示器

LCM：Liquide Crystal Module，液晶显示模组

平时我们在淘宝上买一块液晶屏，插在开发板上就可以直接使用，这种其实是带有芯片（控制器）的LCM液晶模组。

液晶模组是包含液晶以及液晶显示屏下面的各种配件，比如触摸、背光、控制器（以及对应的外围电路），甚至还集成了字库、图片等。

简单来说：LCM包含LCD，以及对应的外围器件。

如何快速开发炫酷的界面

对于很多做过GUI开发的工程师，可能首先想到的就是用GUI实现，比如Qt、 emWin、 LVGL等。

这些GUI能快速开发出酷炫界面吗？当然可以！

但是，对于那些没有用过GUI，甚至不知道什么是GUI的工程师而言，想要快速开发出酷炫界面的的产品，该怎么办？

答案很简单，选择可以二次开发的LCM液晶模组，比如这样的：

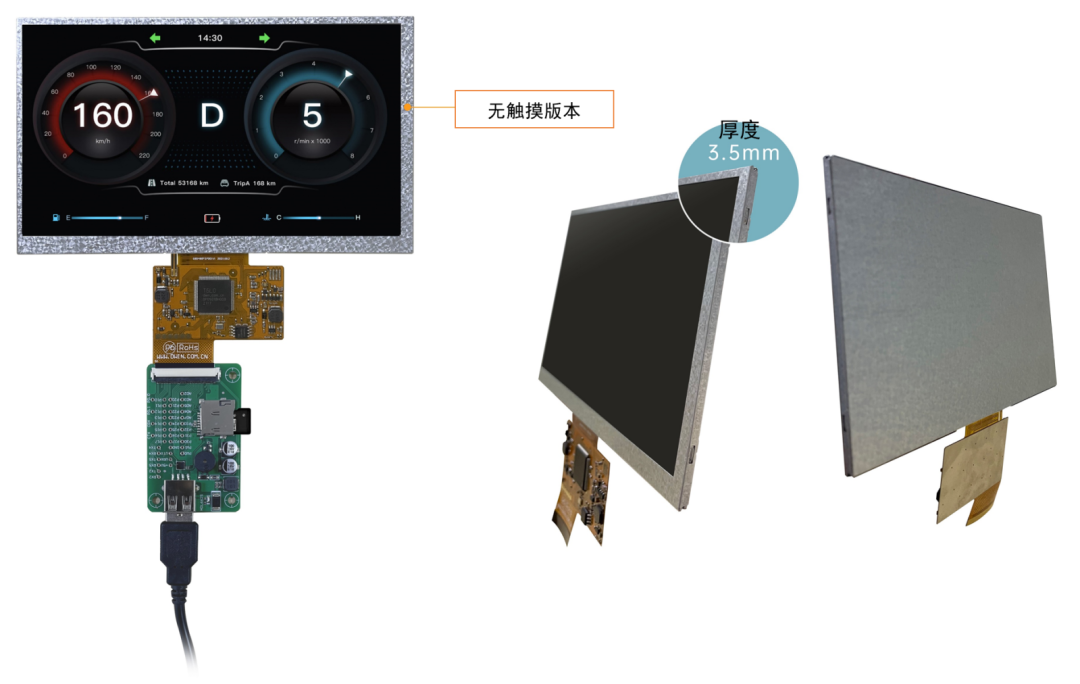
最好自带存储器，可以存储文本、图片等功能的模组。

这种模组就只需要你把酷炫界面（比如：用PS把图片制作好），下载到模组中，通过命令（比如串口指令）控制即可。

对于没有用过GUI的同学来说，这种方法是最快的，只需要熟悉一下通信协议即可（这种通信协议一般很简单，大部分都类似“自定义通信协议”）。

重磅：COF屏0元试用？必须的！

北京迪文屏相关的内容，我之前也多次提到过，也看到有很多小伙伴都在使用迪文屏。

这里给大家重磅推荐一个活动：免费试用迪文智慧屏，并有机会获得1000元现金奖励。

活动时间：即日起到2022.3.31

参与方式：

扫下方 二维码  填写资料申请，大家填写相应的个人收货信息，从哪个渠道看到本次活动（填写芯片之家），简单的项目介绍，记得写50字以上的项目描述，写的越清楚，越容易获得免费试用！

扫码试用

分享试用心得：

申请者需在迪文开发者论坛（http://inforum.dwin.com.cn:20080/forum.php）分享试用心，基于样品开发出应用案例且在论坛开源的用户可获得1000元现金奖励！

迪文COF智能屏介绍

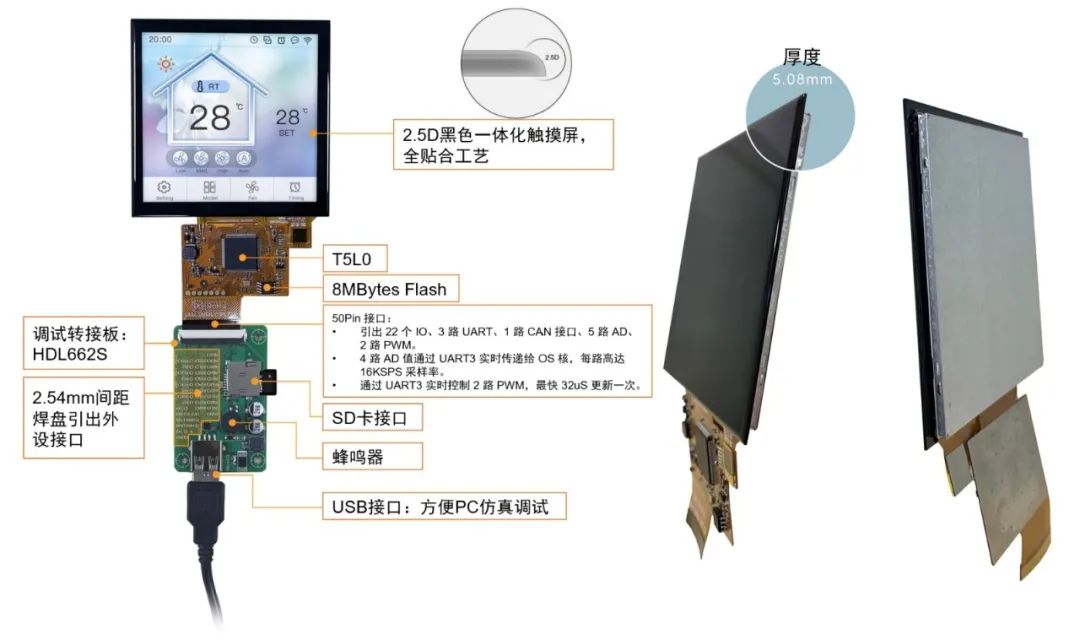
申请试用产品为迪文COF智能屏，是基于迪文低功耗双核T5L0 ASIC，将整个智能屏核心电路放到液晶模组FPC上，集成整合触摸屏，并把用户CPU核的IO、UART、CAN、AD、PWM等接口引出到FPC接口上的产品。产品的GUI通过DGUS平台基于图片素材进行开发，用户系统通过OS核基于标准8051开发。（附产品型号表和形态图）

产品型号：

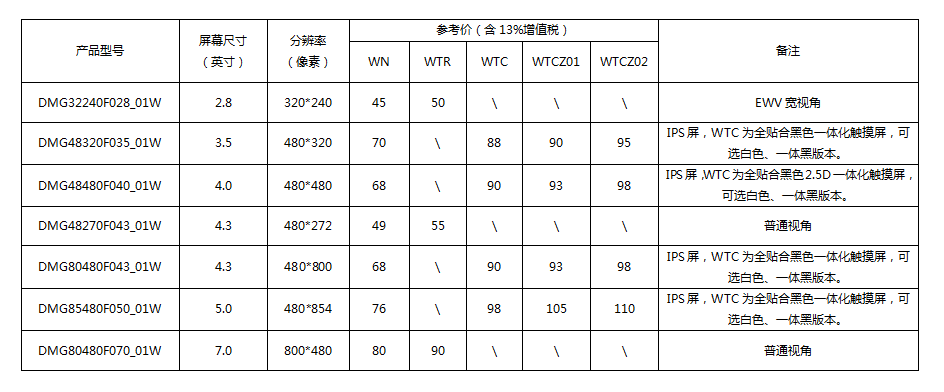
产品形态：

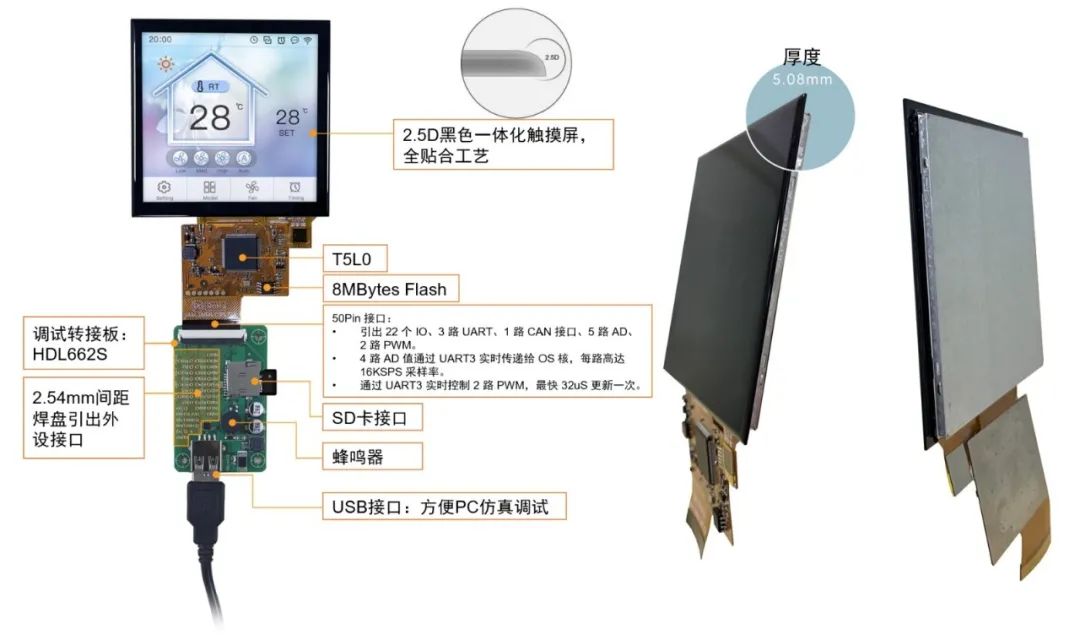
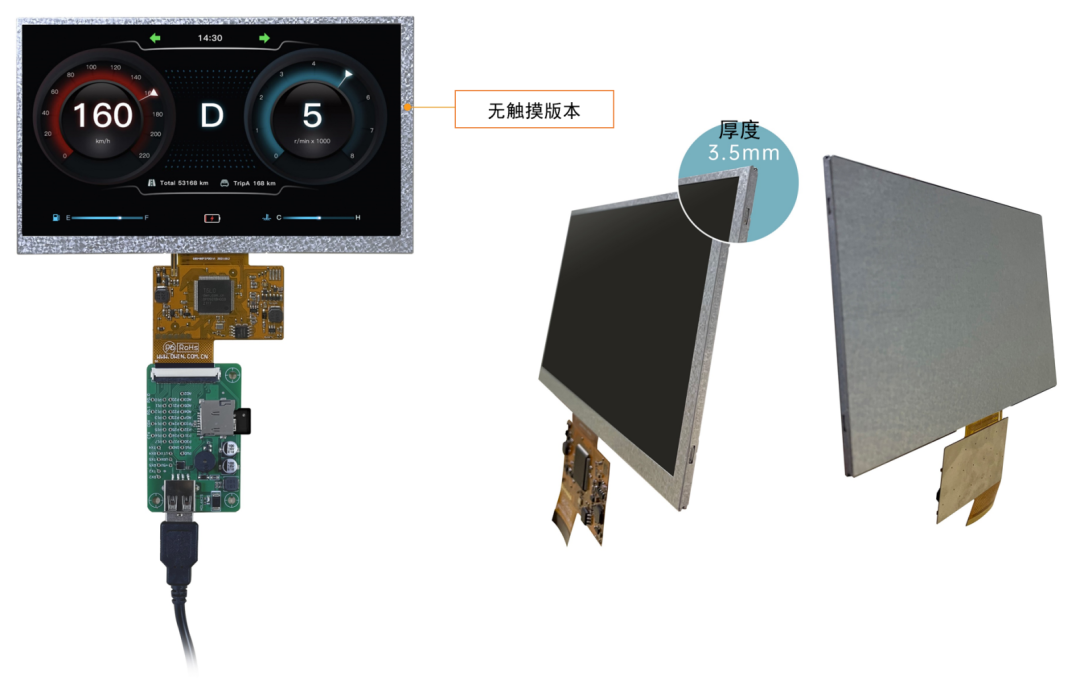
产品优势：结构轻薄、工作环境温和、成本要求苛刻。

迪文COF智能屏 应用资料 等在迪文官网（www.dwin.com.cn）或者迪文开发者论坛（http://inforum.dwin.com.cn:20080/forum.php）下载！点击 阅读原文 直达论坛！