ACM实训冲刺第八天

本文主要是介绍ACM实训冲刺第八天，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【碎碎念】由于昨天做的题都有思路，加上今天有点疲惫，故今天先不复习了，直接开始今天的算法学习

Tokitsukaze and All Zero Sequence

问题

思路

读入测试用例数：首先读取一个整数t，表示接下来会有t组数据需要处理。
遍历每个测试用例：对于每组数据，先读取序列的长度n，然后读取这n个整数到数组中，并使用另一个数组a来统计每个数字出现的次数。
检查重复与计算结果：
- 如果数组中有数字0出现，直接计算并输出非零数字的个数。
- 否则，根据是否有其他重复数字（通过标志变量flag判断），决定输出序列长度加1（无重复）或保持原长度（有重复）。

代码

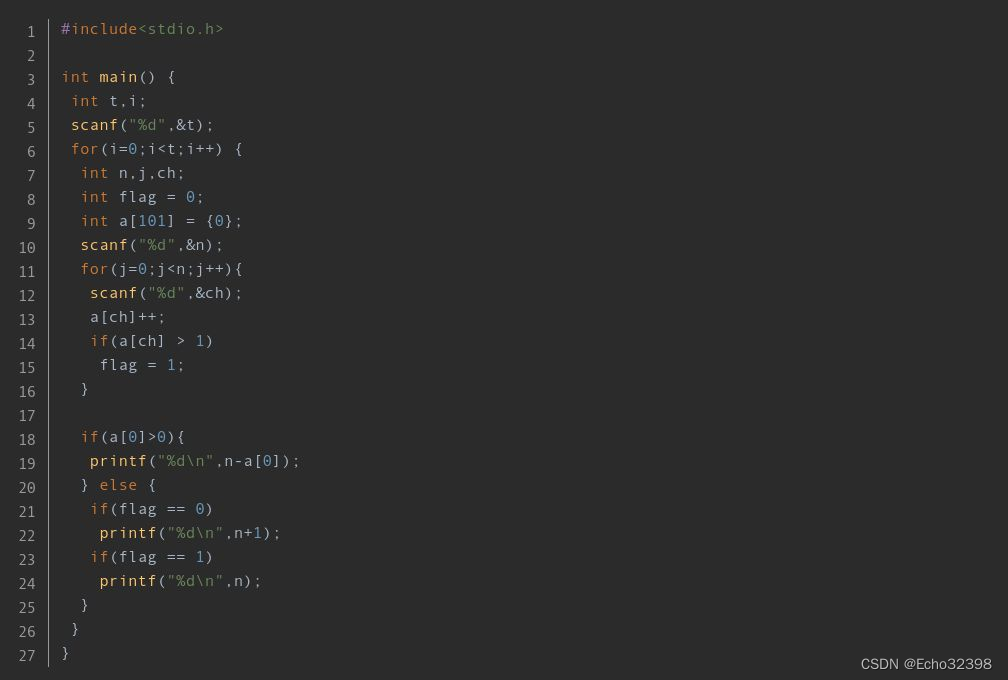
#include<stdio.h>
int main(){// 第一行输入用例数量t int t;scanf("%d",&t) ; // 读取测试用例数量// 遍历t个用例for(int i =0; i<t; i++) {int n; // 序列a的长度int flag=0; // 初始化标志变量，用于记录是否有重复元素，默认假设无重复int ch; // 临时变量，用于存储当前读取的元素值int a[101]={0}; // 初始化数组，用于统计各元素出现次数，长度设置为101以容纳可能的输入值（0-100）// 输入当前序列的长度scanf("%d",&n) ;// 读取并处理序列中的每个元素for(int j=0; j<n; j++){scanf("%d",&ch); // 读取序列中的一个元素a[ch]++; // 对应元素的计数加一，实现统计各元素出现次数// 检查当前元素是否已出现过，若有则设置flag为1表示有重复if(a[ch]>1)flag = 1;	}// 根据条件输出结果if(a[0]>0){ // 若存在0，则计算非零元素个数printf("%d\n",n-a[0]); // 输出非零元素数量}else{// 若没有0，根据是否有重复决定输出结果if(flag==0) // 无重复元素printf("%d\n",n+1); // 序列本身长度加1if(flag==1) // 存在重复元素printf("%d\n",n); // 直接输出原序列长度}}
}

Aggressive cows

问题

农夫约翰建了一个新的长谷仓，有N (2 <= N <= 100,000)个牲口棚。摊位沿直线排列在x1，…，xN (0 <= xi <= 1,000,000,000)。

他的C (2 <= C <= N)头奶牛不喜欢这种谷仓布局，一旦被关进牛栏，它们就会互相攻击。为了防止奶牛互相伤害，FJ想把奶牛分配到牛栏里，这样它们之间的最小距离就尽可能的大。最大的最小距离是多少?
输入
*第一行:两个空格分隔的整数:N和C

*第2行…N+1:第i+1行包含一个整数摊位位置xi
输出
*第一行:一个整数:最大的最小距离

思路

我的潦草思路：感觉有点类似于路灯问题

其他人的代码思路 经过验证代码有误，只需参照思路注释即可

//其他人的思路代码，不过输入输出格式有出入
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
using namespace std;int a[100],n,c;bool fun(int m){//只要相隔m的牛的个数多余实际牛的个数，就可以返回trueint cnt = 1,cur = 0,next=1;//cur是当前牛编号，next是下一只牛的编号，cnt是用来计数的while(next<n){next++;//指向下一只牛if(a[next]-a[cur]>=m){//当前编号牛的位置与下一编号牛的位置只要大于mcnt++;//满足条件的牛的个数加1cur=next;//把当前牛调整为next}}if(cnt>=c)return true;//只要相隔m的牛的个数多余实际牛的个数，就可以返回trueelse return false;
}int main ()
{printf("please input the number of room:");scanf("%d",&n);for(int i=0;i<n;i++){scanf("%d",&a[i]);}printf("input the number of cow: ");scanf("%d",&c);int left=1,right=(a[n-1]-a[0])/(c-1);//求解下界是1，就是他们紧挨着的情况，//上界是最大值-最小值除（牛的个数-1），因为两头都可以取值，蓝哥思考一下为什么是牛的个数-1while(left<right){int mid = ((left+right)+1)/2;//精髓，此处是为了确保二分法能取到最右边的数，故要让除二之前先加一，即向上取整if(fun(mid))left=mid;//此处我们需要找到满足条件的最大的值，所以如果mid点满足条件，要让left=mid，继续找更大的点else right=mid-1;}cout<<"the answer is : "<<left<<endl;printf("the answer is :%d",left);//最后一次求得的满足条件的值mid，已经赋给了left，做一输出leftreturn 0;
}

代码

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
using namespace std;int a[100], n, c;// 方法函数：判断是否能在最小间隔为m的情况下放置至少c个摊位
bool fun(int m) { // 只要相隔m的牛的个数多余实际牛的个数，就可以返回trueint cnt = 1, cur = 0, next = 1; // 初始化计数器、当前牛位置和下一个牛位置while (next < n) {next++; // 移动到下一个牛的位置if (a[next] - a[cur] >= m) { // 检查当前牛与下一牛之间距离是否大于等于mcnt++; // 计数器加1，表示找到了一个符合条件的位置cur = next; // 更新当前牛的位置为下一个牛的位置}}if (cnt >= c) return true; // 如果找到的位置数大于等于c，则返回true，表示可行else return false; // 否则返回false
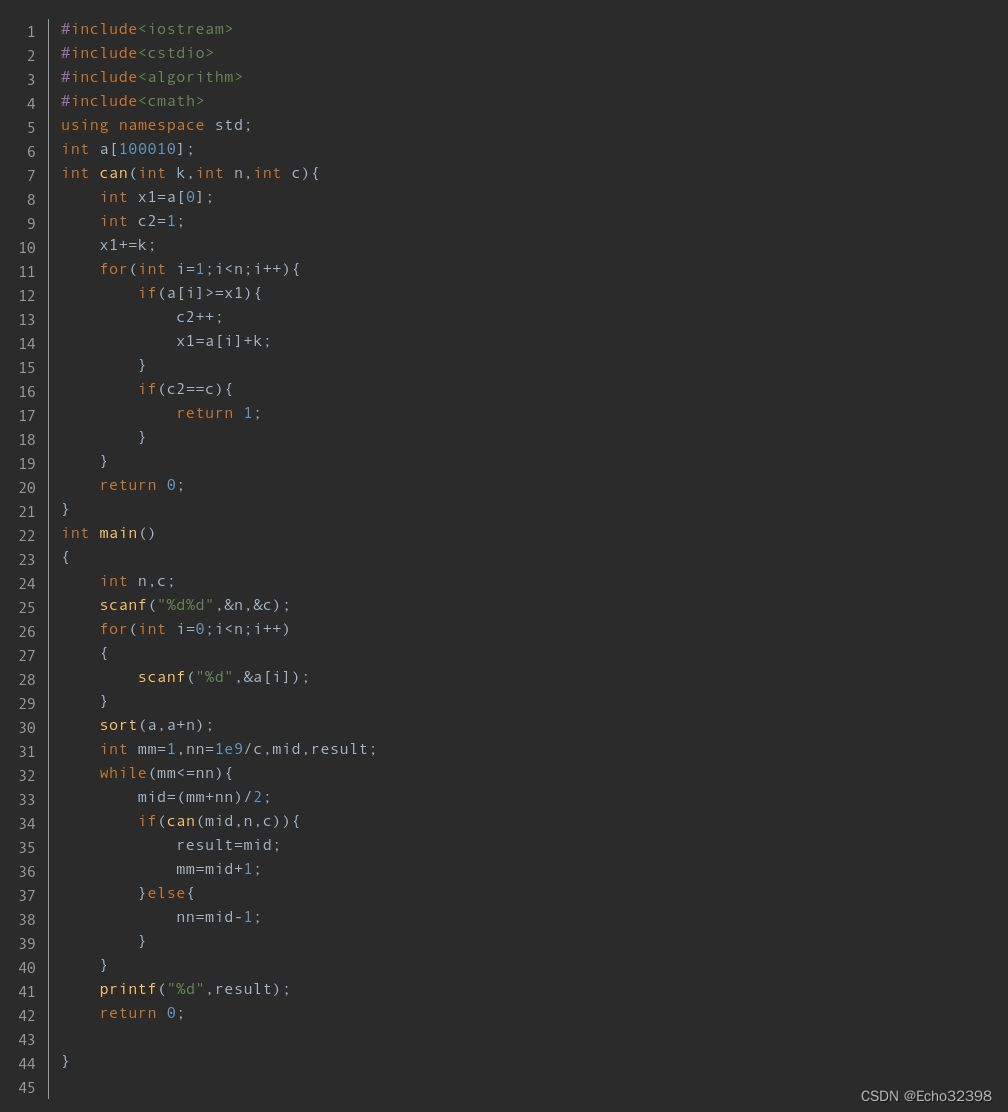
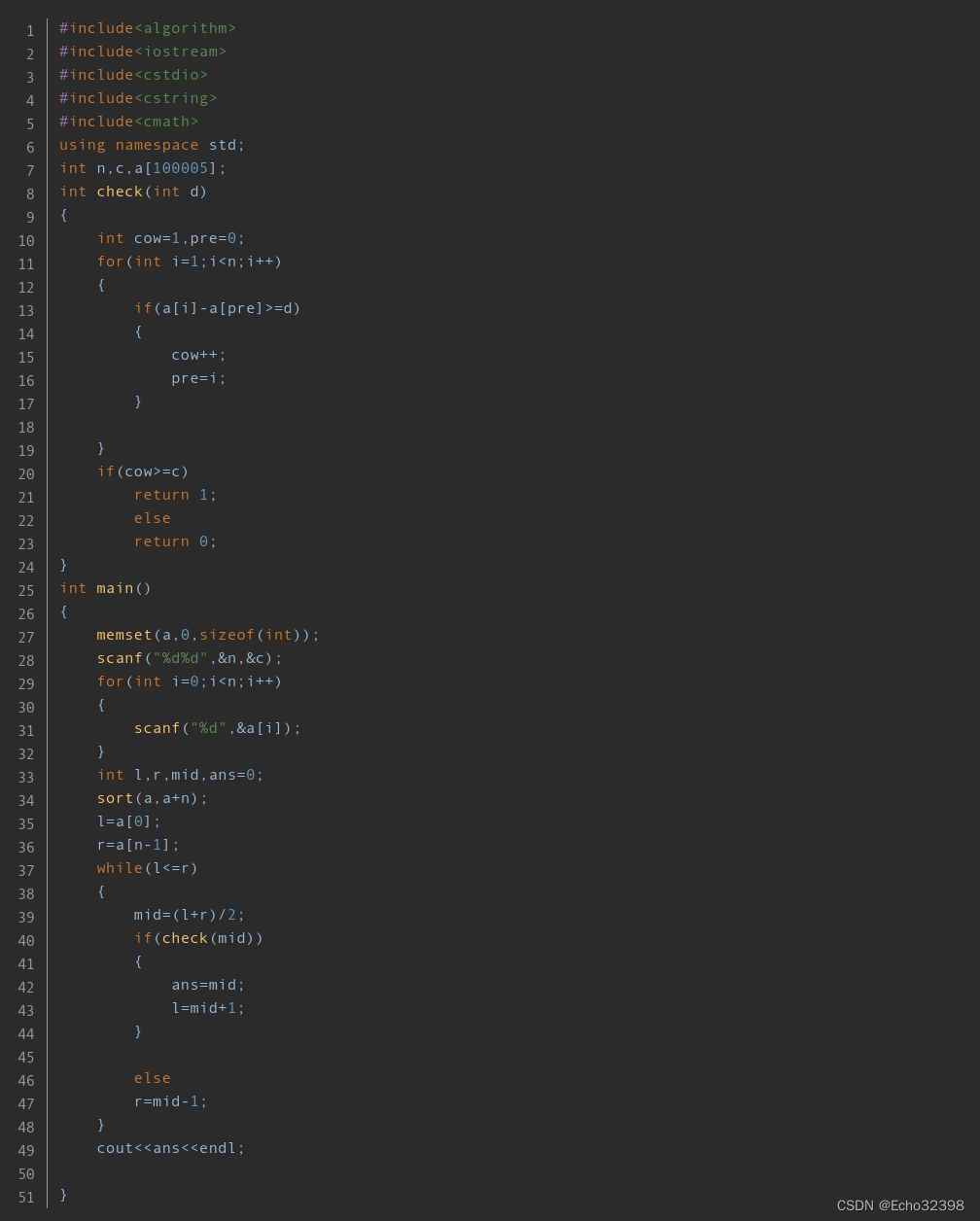
}int main() {// 输入：第一行包含两个空格分隔的整数，N（牛的数量）和C（至少需要的摊位数）scanf("%d%d", &n, &c);// 接下来N行，每行一个整数，表示每头牛所在位置for (int i = 0; i < n; i++) {scanf("%d", &a[i]);}// 初始化二分查找范围（最小距离的上下界）int left = a[0], right = a[n - 1];int ans = 0; // 用于存储最终答案，即最小满足条件的距离// 对位置数组进行排序，以便进行二分查找sort(a, a + n);// 二分查找过程while (left < right) {int mid = ((left + right) + 1) / 2; // 计算中间值，向上取整确保能探索到所有可能if (fun(mid)) { // 如果以mid为最小间隔可以放置c个或更多摊位ans = mid; // 更新答案left = mid + 1; // 缩小搜索区间到右半部分} else {right = mid - 1; // 否则，缩小搜索区间到左半部分}}// 输出最终答案，即最小满足条件的摊位间距printf("%d", ans);return 0;
}