本文主要是介绍C++笔试强训day24,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
1.判断是不是平衡⼆叉树
2.最大子矩阵
3.小葱的01串
1.判断是不是平衡⼆叉树
链接

简单递归即可。
class Solution {
public:// 高度int hight(TreeNode* pRoot){if (pRoot == nullptr)return 0;int l = hight(pRoot->left);int r = hight(pRoot->right);return max(l, r) + 1;}// 检查是否为平衡二叉树bool Check(TreeNode* pl, TreeNode* pr){if (abs(hight(pl) - hight(pr)) <= 1)return true;return false;}bool IsBalanced_Solution(TreeNode* pRoot) {if (!pRoot)return true;if (Check(pRoot->left, pRoot->right))return IsBalanced_Solution(pRoot->left) && IsBalanced_Solution(pRoot->right);elsereturn false;}
};2.最大子矩阵
链接

我的思路是构建二维前缀和,然后再遍历所有的子矩阵,但是我遍历子矩阵有错误,没遍历到全部,所有一直过不了。
完整代码:

(我这里是从1开始遍历的)

#include <iostream>
using namespace std;
const int sta = 110;
int N;
int arr[sta][sta];
int sum[sta][sta];
int main() {cin >> N;for (int i = 1; i <= N; ++i)for (int j = 1; j <= N; ++j)cin >> arr[i][j];// 构建前缀和for (int i = 1; i <= N; ++i)for (int j = 1; j <= N; ++j)sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + arr[i][j];// 枚举int ret = -127 * N;for (int x1 = 1; x1 <= N; ++x1)for (int y1 = 1; y1 <= N; ++y1)for (int x2 = x1; x2 <= N; ++x2) for(int y2 = y1; y2 <= N; ++y2)if(ret < sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1])ret = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];cout << ret << endl;return 0;
}3.小葱的01串
链接

固定滑动窗口,每次都遍历长度为n / 2的窗口。
#include <iostream>
using namespace std;int n;
int cnt[2];
string s;
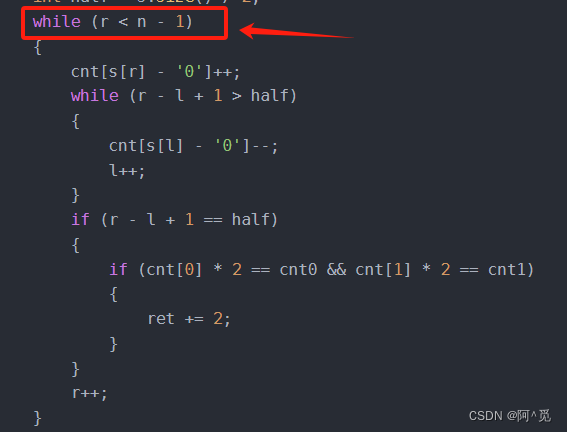
int main() {cin >> n;cin >> s;int cnt0 = 0, cnt1 = 0;for (auto c : s){if (c == '0')cnt0++;elsecnt1++;}int l = 0, r = 0, ret = 0;int half = s.size() / 2;while (r < n - 1){cnt[s[r] - '0']++;while (r - l + 1 > half){cnt[s[l] - '0']--;l++;}if (r - l + 1 == half){if (cnt[0] * 2 == cnt0 && cnt[1] * 2 == cnt1){ret += 2;}}r++;}cout << ret << endl;return 0;
}因为每次遍历一半的数量时,另一半也是满足条件的,所有每次符合条件可以 将 ret += 2 (ret为返回结果)
但是有一个例外:

当其为从0开始的前一半的数时,防止其重复遍历另一半,因此r 应该 < n - 1。
这篇关于C++笔试强训day24的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





