本文主要是介绍Diffie-Hellman密钥交换协议,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Diffie-Hellman也就是DH算法,本章我们将简单介绍一下该算法。
什么是DH算法?
DH算法是Diffie和Hellman两位作者于1976年提出的一种密钥交换协议。它的主要用途是在非安全网络下通信双方密钥的安全建立,从而使通信双方能够使用这个密钥进行消息的加密解密,从而实现通信的安全。DH算法实现的是密钥交换或者密钥协商,通信双方各自生成自己的私钥和公钥,私钥仅对自己可见,然后交换公钥,并根据自己的私钥和对方的公钥,生成最终的密钥secretKey,DH算法通过数学定律保证了双方各自计算出的secretKey是相同的
在基于对称加密进行安全通信的过程中,通信双方需要持有一个共享的密钥。只有这样,由任何一方加密的信息才能由另一方使用相同的密钥解密。
但是在能够安全的通信之前,通信双方应该如何约定一个共享的密钥呢?这就是安全中的经典问题:密钥配送问题。
常用的加密算法
对称加密算法
流加密(序列密码算法)
分组加密
常用的对称加密算法:DES/3DES、AES
非对称加密算法
RSA 支持变长密钥的公共密钥算法
DH算法的计算过程
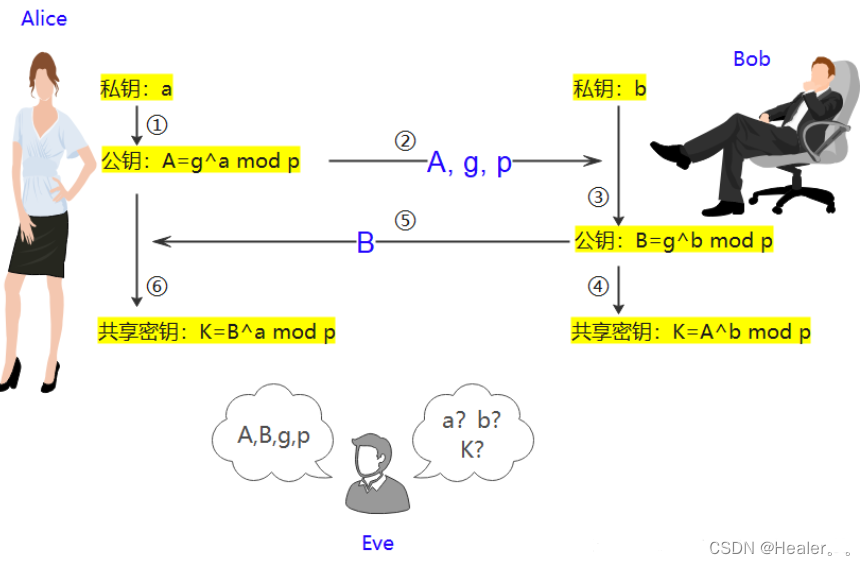
Alice和Bob都有一个只有自己知道的私钥,在特定规则(g, a, p)下生成自己的公钥A;
Alice将自己的公钥A,连同g, p共同发给Bob
Bob在收到Alice发送来的公钥A, g, p后,先使用相同的规则((g, a, p))生成自己的公钥B;
再使用Alice的公钥A计算生成共享密钥K
Bob将自己的公钥B发送给Alice即可。(Alice已经有g, p, 因此无需在发送)
Alice在接收到Bob的公钥B后,使用相同的规则计算成功共享密钥K
至此,Alice 和 Bob便同时拥有了共享密钥K。此时由于各自的私钥a,b未在互联网上传播,因此即使存在窥探者Eve,他仅通过公开的A\B\g\p在短时间内无法破解出a,b,K。
因此DH算法便可以在不安全的网络上协商出密钥,基于此构建安全的加密通道。
看到这里可能还是有点懵,所以这里我们就不聊数学原理,因为实际情况太过于复杂,我们就以一种简单的计算案例来进行理解整个DH算法的过程。

我们一步一步的来理解。
这里的P是一个质数,正常环境下一般比较大,可以将其进行公开。
g是一个DH算法中所固定的一个数(是一个双方已知的值)。
x和y为A、B双方自己所知道的一个随机值,正常环境中一般比较大。
X和Y时经过A和B双方根据自身已有的值来运算出来的值,将这两个值计算出后,再互相发送给对方进行二次计算。
最后双方经过公式计算出来的Z是相同的。
也就是说,Z就是双方经过DH算法协商出来的密钥。
该算法的好处在于,黑客根据已公开的数据(P,g,X,Y),难以推导出x、y,因为是取模运算,是不可逆的。而且正常环境下P和x,y的值都非常大,这也使破解难度加大。协商出来的Z,在A、B通信时,传输的相当于就是一个对称密钥,相当于是A、B之间进行一个私密的传输,不会造成密钥泄露,而导致中间人劫持(因为A、B双方都不会把协商的密钥Z发出,只会用Z对数据进行加密和解密)
注意:真实情况下这样的密钥协商可能会进行很多次,以达到更高的安全性和可靠性。
这篇关于Diffie-Hellman密钥交换协议的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






