本文主要是介绍Codeforces Round #308 (Div. 2) E. Vanya and Brackets,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Vanya is doing his maths homework. He has an expression of form 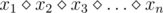 , where x1, x2, ..., xn are digits from 1 to 9, and sign
, where x1, x2, ..., xn are digits from 1 to 9, and sign  represents either a plus '+' or the multiplication sign '*'. Vanya needs to add one pair of brackets in this expression so that to maximize the value of the resulting expression.
represents either a plus '+' or the multiplication sign '*'. Vanya needs to add one pair of brackets in this expression so that to maximize the value of the resulting expression.
The first line contains expression s (1 ≤ |s| ≤ 5001, |s| is odd), its odd positions only contain digits from 1 to 9, and even positions only contain signs + and * .
The number of signs * doesn't exceed 15.
In the first line print the maximum possible value of an expression.
3+5*7+8*4
303
2+3*5
25
3*4*5
60
Note to the first sample test. 3 + 5 * (7 + 8) * 4 = 303.
Note to the second sample test. (2 + 3) * 5 = 25.
Note to the third sample test. (3 * 4) * 5 = 60 (also many other variants are valid, for instance, (3) * 4 * 5 = 60).
题目要求对一个只有加号乘号的数式加一对括号,要求和最大是多少,*的个数不超过15个,这个问题如果枚举至少也o(n^3),所以复杂度太高,考虑到
*号的个数很少,就可以想到(一定在*号的右边或开始,)一定在*的左边或开始,因为,如果存在这样的式子+(...)+,这括号加的没有意义,不能使等式
变大,如果存在*(....)+这样的式子,我们把)向右移可使式子变大,如果存在+(...)*,我们可以把(向左移使得式子变大,这样,枚举一下,总的复杂度为n*17*17个,足够了!
#define INF 9000000000000000000
#define EPS (double)1e-9
#define mod 1000000007
#define PI 3.14159265358979
//*******************************************************************************/
#endif
#define N 5005
#define MOD 1000000007
int n,len,leftt[30],leftnum,rightt[30],rightnum;
long long ans;
char str[N],temp[N];
stack<char> opS;
stack<long long> numS;
int getNum(char c){if(c == '(')return 3;else if(c == '*')return 2;else if(c == '+')return 1;else if(c == ')')return 0;return -1;
}
bool isdigit(char c){if(c>='0' && c<='9')return true;return false;
}
bool PopCal(){char op = opS.top();opS.pop();//cout<<op<<endl;if(op == '+'){long long num1 = numS.top();numS.pop();long long num2 = numS.top();numS.pop();numS.push(num1 + num2);}else if(op == '*'){long long num1 = numS.top();numS.pop();long long num2 = numS.top();numS.pop();numS.push(num1 * num2);}elsereturn true;return false;
}
long long cal(char s[],int l){while(!opS.empty()) opS.pop();while(!numS.empty()) numS.pop();for(int i=0;i<l;i++){if(isdigit(s[i]))numS.push(s[i]-'0');else {while(!opS.empty() && getNum(s[i]) <= getNum(opS.top())){if(opS.top() == '(' && s[i]!=')')break;if(PopCal())break;}if(s[i] != ')')opS.push(s[i]);}}while(!opS.empty()){PopCal();}return numS.top();
}
int main()
{//cout<<cal("3+5*(7+8)*4",11);while (SS(str) != EOF){len = strlen(str);leftnum = 0;rightnum = 0;leftt[leftnum++] = -1;ans = 0;FI(len){if(str[i] == '*'){leftt[leftnum++] = i;rightt[rightnum++] = i;}}rightt[rightnum++] = len;FI(leftnum)FJ(rightnum){if(rightt[j] > leftt[i]){int count = 0;if(leftt[i] == -1) temp[count++] = '(';for(int k=0;k<len;k++){if(k == leftt[i]){temp[count++] = str[k];temp[count++] = '(';}else if(k == rightt[j]){temp[count++] = ')';temp[count++] = str[k];}else {temp[count++] = str[k];}}if(rightt[j] == len) temp[count++] = ')';temp[count] = '\0';//printf("%d %d %d %d %s ",i,j,leftt[i],rightt[j],temp);ans = max(ans,cal(temp,len+2));//cout<<cal(temp,len+2)<<endl;}}cout<<ans<<endl;}return 0;
}这篇关于Codeforces Round #308 (Div. 2) E. Vanya and Brackets的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





