【第一周】最大子列和问题整理

本文主要是介绍【第一周】最大子列和问题整理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目地址：01-1. 最大子列和问题

算法一：暴力，直接计算出所有子列和，然后比较，显然复杂度炸裂，O（N^3）

int MaxSubseqSum1(int A[],int N)
{int ThisSum;int MaxSum = 0;int i,j,k;for (i = 0; i < N; ++i)//i是子列左端的位置{for (j = i; j < N; ++j)//j是子列右端的位置{ThisSum = 0;//A[i]到A[j]的子列和for (k = i; k < j ; ++k){ThisSum += A[k];if (ThisSum > MaxSum){MaxSum = ThisSum;}}}}return MaxSum;
}

算法二：优化第三层循环，将复杂度降到O（N^2）

int MaxSubseqSum2(int A[],int N)
{int ThisSum;int MaxSum = 0;int i,j;for (i = 0; i < N; ++i)//i是子列左端的位置{ThisSum = 0;//A[i]到A[j]的子列和for (j = i; j < N; ++j)//j是子列右端的位置{	ThisSum += A[j];//对于相同的i，不同的j，只要在j-1的基础上累加上1项即可if (ThisSum > MaxSum){MaxSum = ThisSum;}}}return MaxSum;
}

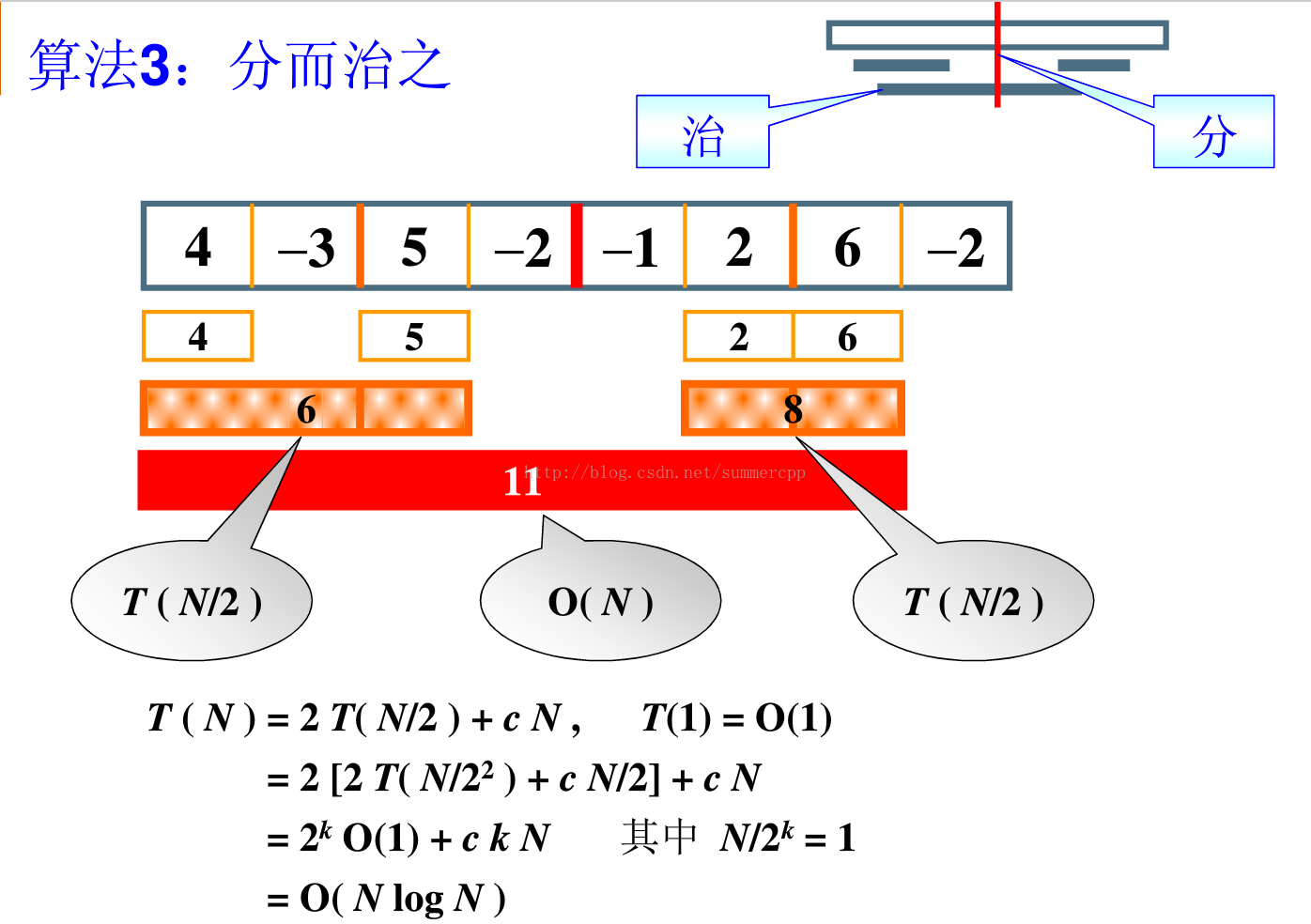
算法三：分而治之，把数组从中间分成两部分，然后递归地解决左右两边，最后考虑跨越边界的最大值。

复杂度的推算：

int MaxSubseqSum3(int A[],int x,int y)
{if (y-x==1){return A[x];}int mid = x+(y-x)/2;int leftSum = 0;int rightSum = 0;int leftMaxValue = A[m-1];int rightMaxValue = A[m];int i;int maxValue=max(MaxSubseqSum3(a,x,m),MaxSubseqSum3(a,m,y));for (i = mid - 1; i >= x; --i){leftSum += A[i];leftMaxValue = max(leftMaxValue,leftSum);}for (i = m; i < y; ++i){rightSum += A[i];rightMaxValue = max(rightMaxValue,rightSum);}return max(maxValue,leftMaxValue+rightMaxValue);}

算法四：在线处理,达到理想的复杂度了，O（N）

int MaxSubseqSum4(int A[],int N)
{int ThisSum,MaxSum;int i;ThisSum = MaxSum = 0;for (i = 0; i < N; ++i){ThisSum += A[i];//向右累加if (ThisSum > MaxSum){MaxSum = ThisSum;}else if (ThisSum < 0){ThisSum = 0;}}return MaxSum;
}

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

最后AC的代码：

#include <cstdio>using namespace std;#define MAXN 100000
int main()
{freopen("in.txt","r",stdin);int list[MAXN];int n,i,;int ThisSum, MaxSum;int head,tail;scanf("%d",&n);int start = 0,end = n-1;for (int i = 0; i < n; ++i){scanf("%d",&list[i]);}	ThisSum = MaxSum = 0;for (int i = 0; i < n; ++i){if (ThisSum >=0){ThisSum += list[i];tail = i;}else{ThisSum = list[i];head = i;tail = i;}if (ThisSum > MaxSum ||(ThisSum == 0 && MaxSum == 0)){MaxSum = ThisSum;start = head;end = tail;}}printf("%d %d %d\n",MaxSum, list[start], list[end]);return 0;
}

这篇关于【第一周】最大子列和问题整理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---