【深耕 Python】Quantum Computing 量子计算机（6）计算＜m|V|n＞数值积分

本文主要是介绍【深耕 Python】Quantum Computing 量子计算机（6）计算＜m|V|n＞数值积分，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

写在前面

往期量子计算机博客：

【深耕 Python】Quantum Computing 量子计算机（1）图像绘制基础

【深耕 Python】Quantum Computing 量子计算机（2）绘制电子运动平面波

【深耕 Python】Quantum Computing 量子计算机（3）重要数学公式一览

【深耕 Python】Quantum Computing 量子计算机（4）量子物理概念（一）

【深耕 Python】Quantum Computing 量子计算机（5）量子物理概念（二）

一、积分定义式

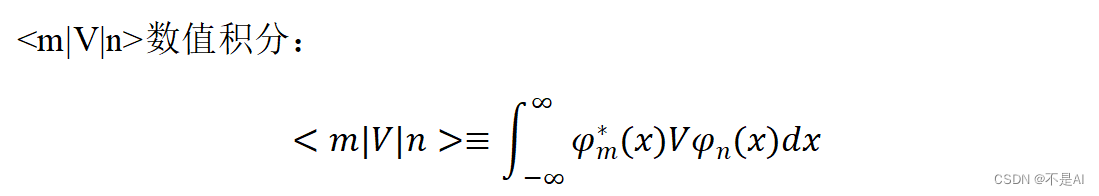
在这里插入图片描述

二、势能公式

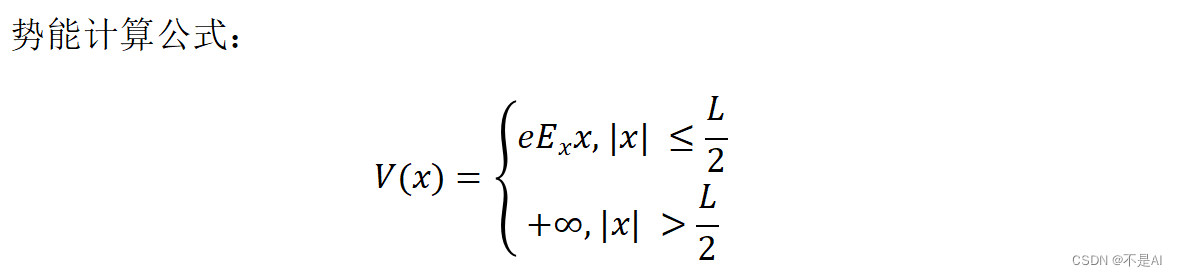
在这里插入图片描述

三、相关常数设置

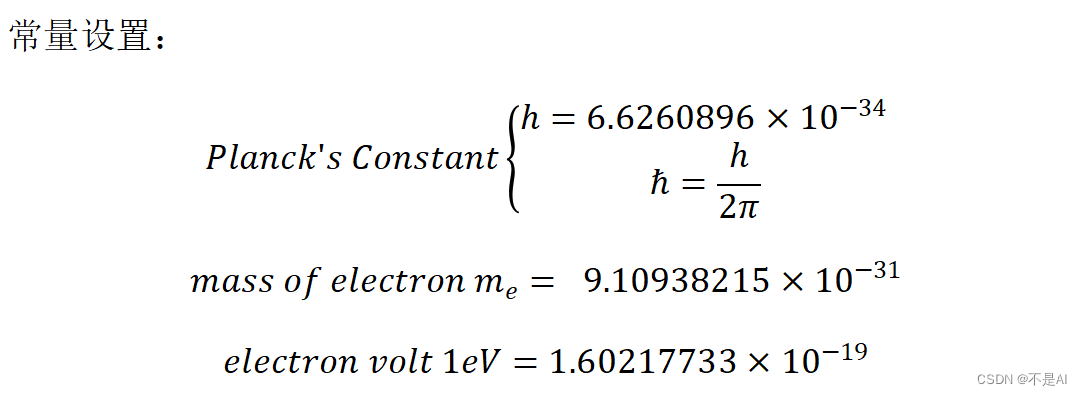
在这里插入图片描述

四、计算数值积分的Python代码

import math
from scipy import integrateh = 6.6260896 * 10 ** -34
hbar = h / (2.0 * math.pi)me = 9.10938215 * 10 ** -31eV = 1.60217733 * 10 ** -19L = 1.0 * 10 ** -9x_min = -L / 2.0
x_max = L / 2.0n_max = 10Ex = 1.0 * 10 ** 10def verphi(n, x):kn = math.pi * (n + 1) / Lreturn math.sqrt(2.0 / L) * math.sin(kn * (x + L / 2.0))def V(x, Ex):return math.e * Ex * xdef integral_matrixElement(x, n1, n2, Ex):return verphi(n1, x) * V(x, Ex) * verphi(n2, x) / eVfor n1 in range(n_max + 1):for n2 in range(n_max + 1):result = integrate.quad(integral_matrixElement, x_min, x_max, args=(n1, n2, Ex))real = result[0]imag = 0print("(" + str(n1) + ", " + str(n2) + ") " + str(real))

积分结果：

(0, 0) 6341.738760657484
(0, 1) -3.056058246357965e+19
(0, 2) 2609.307906875312
(0, 3) -2.4448465970863724e+18
(0, 4) 6870.623927366621
(0, 5) -6.735801849115569e+17
(0, 6) 4827.5805244781905
(0, 7) -2.771934917331456e+17
(0, 8) -14813.886749646688
(0, 9) -1.4031488734426288e+17
(0, 10) -91.85343359174219
(1, 0) -3.056058246357965e+19
(1, 1) 8677.375330811079
(1, 2) -3.3005429060666024e+19
(1, 3) 7559.214463884988
(1, 4) -3.1184267819979377e+18
(1, 5) 8397.13098087583
(1, 6) -9.507736766447043e+17
(1, 7) -11203.391019872324
(1, 8) -4.175083790774072e+17
(1, 9) 2629.7575721982435
(1, 10) -2.2101670420734822e+17
(2, 0) 3305.077150828044
(2, 1) -3.3005429060666024e+19
(2, 2) 4131.0895468288745
(2, 3) -3.3679009245577576e+19
(2, 4) 18393.399430849167
(2, 5) -3.395620273731079e+18
(2, 6) -9305.413780188943
(2, 7) -1.0910885639889608e+18
(2, 8) -425.52945379666164
(2, 9) -4.982101959405064e+17
(2, 10) -2797.4992591219802
(3, 0) -2.444846597086372e+18
(3, 1) 7540.93172754931
(3, 2) -3.3679009245577572e+19
(3, 3) 10871.226664979697
(3, 4) -3.395620273731073e+19
(3, 5) 4636.680523494656
(3, 6) -3.535935161075353e+18
(3, 7) 5349.394079704496
(3, 8) -1.1717903808520607e+18
(3, 9) 18557.06635991661
(3, 10) -5.48843113631636e+17
(4, 0) 6465.045377234563
(4, 1) -3.1184267819979377e+18
(4, 2) 18407.930328892166
(4, 3) -3.395620273731072e+19
(4, 4) 5278.177294867377
(4, 5) -3.4096517624654983e+19
(4, 6) -10654.575490810419
(4, 7) -3.6166369779384207e+18
(4, 8) -3997.905026982768
(4, 9) -1.2224232985431992e+18
(4, 10) -2426.58163543784
(5, 0) -6.735801849115574e+17
(5, 1) 6890.926988234758
(5, 2) -3.3956202737310833e+18
(5, 3) 4534.457182746286
(5, 4) -3.4096517624654983e+19
(5, 5) 3642.5609606579337
(5, 6) -3.4177219441518076e+19
(5, 7) 10615.200195340132
(5, 8) -3.66726989562957e+18
(5, 9) 25011.51925503606
(5, 10) -1.2562620057692713e+18
(6, 0) 6183.626968714323
(6, 1) -9.507736766447043e+17
(6, 2) -9718.696863996012
(6, 3) -3.5359351610753536e+18
(6, 4) -10105.641181736304
(6, 5) -3.4177219441518076e+19
(6, 6) 3897.1842703463662
(6, 7) -3.4227852359209206e+19
(6, 8) -8550.64335308177
(6, 9) -3.7011086028556754e+18
(6, 10) -9318.227951041345
C:\Users\lycbu\Desktop\Python 量子计算机\Day 7\quantumWell_StarkEffect_step1.py:36: IntegrationWarning: The occurrence of roundoff error is detected, which prevents the requested tolerance from being achieved.  The error may be underestimated.result = integrate.quad(integral_matrixElement, x_min, x_max, args=(n1, n2, Ex))
(7, 0) -2.7719349173314662e+17
(7, 1) -11746.815843769886
(7, 2) -1.0910885639889618e+18
(7, 3) 4746.182689685192
(7, 4) -3.6166369779384197e+18
(7, 5) 10939.680098040822
(7, 6) -3.42278523592092e+19
(7, 7) 30312.39957168161
(7, 8) -3.426169106643533e+19
(7, 9) 59630.42734047828
(7, 10) -3.7248355357271296e+18
(8, 0) -14763.958321932972
(8, 1) -4.175083790774057e+17
(8, 2) 376.26024772313724
(8, 3) -1.171790380852062e+18
(8, 4) -2891.430230791178
(8, 5) -3.667269895629572e+18
(8, 6) -9035.816467070696
(8, 7) -3.4261691066435334e+19
(8, 8) 19862.976591607174
(8, 9) -3.4285417999306818e+19
(8, 10) -54641.972971282514
(9, 0) -1.4031488734426315e+17
(9, 1) 1654.2331507959864
(9, 2) -4.982101959405055e+17
(9, 3) 17653.776341955723
(9, 4) -1.222423298543198e+18
(9, 5) 27534.81059036405
(9, 6) -3.7011086028556774e+18
(9, 7) 58372.822664076666
(9, 8) -3.4285417999306818e+19
(9, 9) 5452.609965541867
(9, 10) -3.430269460197712e+19
(10, 0) -269.7846480739375
(10, 1) -2.2101670420734925e+17
(10, 2) -4534.741401922178
(10, 3) -5.488431136316375e+17
(10, 4) -2159.696443591254
(10, 5) -1.2562620057692713e+18
(10, 6) -8252.286148308438
(10, 7) -3.724835535727129e+18
(10, 8) -55910.908016360045
(10, 9) -3.430269460197712e+19
(10, 10) -275.15859882778125Process finished with exit code 0