10.轮转数组

本文主要是介绍10.轮转数组，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

大家好，我是晓星航。今天为大家带来的是 轮转数组 相关的讲解！😀

题目简介

题目解答

解法一：使用额外的数组

思路：我们可以使用额外的数组来将每个元素放至正确的位置。用 n 表示数组的长度，我们遍历原数组，将原数组下标为 i 的元素放至新数组下标为 (i+k) mod n 的位置，最后将新数组拷贝至原数组即可。

代码：

class Solution {public void rotate(int[] nums, int k) {int n = nums.length;int[] newArr = new int[n];for (int i = 0; i < n; ++i) {newArr[(i + k) % n] = nums[i];}System.arraycopy(newArr, 0, nums, 0, n);}
}

这里直接从反转位置开始填入数组元素，可以形象理解为我们把起点改变为了i+k，然后我们在把数组后面填满后再从下标为0的位置开始继续填充元素。(i+k)%n的意义即使在nums数组后面填满后，然后从第一个位置继续填充。

这里方法的含义是：我们从数组newArr的0下标开始，复制到nums数组从0下标开始，复制n个元素。

复杂度分析：

时间复杂度： O(n)，其中 n 为数组的长度。

空间复杂度： O(n)。

---

解法二：数组反转

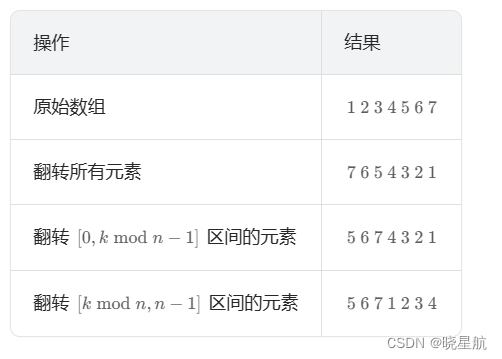
思路：我们直接拿官方的图解就可以很轻易地看出思路

代码：

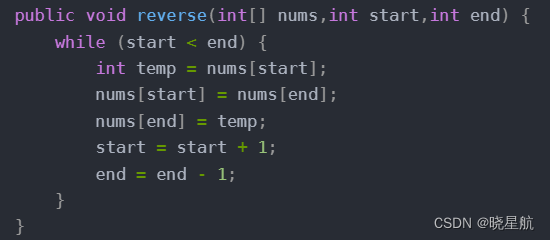
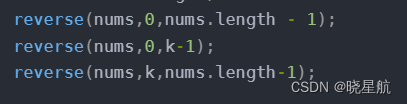
class Solution {public void reverse(int[] nums,int start,int end) {while (start < end) {int temp = nums[start];nums[start] = nums[end];nums[end] = temp;start = start + 1;end = end - 1;}}public void rotate(int[] nums, int k) {k = k % nums.length;reverse(nums,0,nums.length - 1);reverse(nums,0,k-1);reverse(nums,k,nums.length-1);}
}

一个很简单的反转数组全部元素的代码：

这里k模数组长度的作用就是为了避免要轮转的元素个数比数组本身还大，既然轮转一周等于没有轮转，因此我们采取这个方法避免数组越界的问题。

这三次轮转的作用也很好解释，第一次先把数组整个反转。第二次将前半段反转，第三次将后半段反转，这样就符合题意了，数组是由两个递增数组组合而成。

复杂度分析：

时间复杂度：O(n)，其中 n 为数组的长度。每个元素被翻转两次，一共 n 个元素，因此总时间复杂度为 O(2n)=O(n)。

空间复杂度：O(1)。

题目链接

感谢各位读者的阅读，本文章有任何错误都可以在评论区发表你们的意见，我会对文章进行改正的。如果本文章对你有帮助请动一动你们敏捷的小手点一点赞，你的每一次鼓励都是作者创作的动力哦！😘

这篇关于10.轮转数组的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---