百度之星资格赛——Disk Schedule（双调旅行商问题）

本文主要是介绍百度之星资格赛——Disk Schedule（双调旅行商问题），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Disk Schedule

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 2368 Accepted Submission(s): 333

Problem Description

有很多从磁盘读取数据的需求，包括顺序读取、随机读取。为了提高效率，需要人为安排磁盘读取。然而，在现实中，这种做法很复杂。我们考虑一个相对简单的场景。磁盘有许多轨道，每个轨道有许多扇区，用于存储数据。当我们想在特定扇区来读取数据时，磁头需要跳转到特定的轨道、具体扇区进行读取操作。为了简单，我们假设磁头可以在某个轨道顺时针或逆时针匀速旋转，旋转一周的时间是360个单位时间。磁头也可以随意移动到某个轨道进行读取，每跳转到一个相邻轨道的时间为400个单位时间，跳转前后磁头所在扇区位置不变。一次读取数据的时间为10个单位时间，读取前后磁头所在的扇区位置不变。磁头同时只能做一件事：跳转轨道，旋转或读取。现在，需要在磁盘读取一组数据，假设每个轨道至多有一个读取请求，这个读取的扇区是轨道上分布在 0到359内的一个整数点扇区，即轨道的某个360等分点。磁头的起始点在0轨道0扇区，此时没有数据读取。在完成所有读取后，磁头需要回到0轨道0扇区的始点位置。请问完成给定的读取所需的最小时间。 

Input

输入的第一行包含一个整数M（0<M<=100），表示测试数据的组数。 
 对于每组测试数据，第一行包含一个整数N（0<N<=1000），表示要读取的数据的数量。之后每行包含两个整数T和S（0<T<=1000，0<= S<360），表示每个数据的磁道和扇区，磁道是按升序排列，并且没有重复。 
 

Output

对于每组测试数据，输出一个整数，表示完成全部读取所需的时间。 

Sample Input

3

1

1 10  

3

1 20  

3 30 

5 10 

2

1 10 

2 11 

Sample Output

830 4090 1642 

题解：参照欧几里德旅行商问题只需把本题中的两个点的距离用（距离=两点的轨道差*400+两点的扇区差）代替即可；

需要注意的是扇区差是轨道小弧的长度：即(360+a[j].y-a[i].y)%360与abs(a[i].y-a[j].y)的较小者，如扇区350与扇区10的距离是20而不是340；

还有一点就是要把起点（0，0）加上；

下面是转自大神们的欧几里德旅行商问题的思路；链接http://blog.csdn.net/weyuli/article/details/19752217

其实所谓的欧几里德旅行商问题就是从1到n 然后在从n到1的最短路，去的时候经过的点的顺序必须从小到大，来的时候经过的点的顺序必须从大到小，并且每个点只能经过一次(1和n不算)，输出最短路的长度。

思路【转】：

欧几里得旅行商问题是对平面上给定的n个点确定一条连接各点的最短闭合旅程的问题。如图（a）给出了一个7个点问题的解。这个问题的一般形式是NP完全的，故其解需要多于多项式的时间。

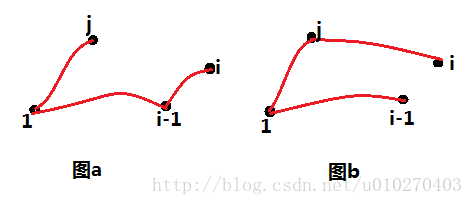
J.L. Bentley 建议通过只考虑双调旅程(bitonic tour)来简化问题,这种旅程即为从最左点开始，严格地从左到右直至最右点，然后严格地从右到左直至出发点。下图(b)显示了同样的7个点的最短双调路线。在这种情况下，多项式的算法是可能的。事实上，存在确定的最优双调路线的O(n*n)时间的算法。

图a

图b

注:在一个单位栅格上显示的平面上的七个点。 a)最短闭合路线,长度大约是24.89。这个路线不是双调的。b)相同点的集合上的最短双调闭合路线。长度大约是25.58。

这是一个算导上的思考题15-1。

首先将给出的点排序，关键字x，重新编号，从左至右1，2，3，…，n。

定义d[i][j]，表示结点i到结点j之间的距离。

定义dp[i][j]，表示从i连到1，再从1连到j，（注意，i>j，且并没有相连。）

对于任意一个点i来说，有两种连接方法，一种是如图（a）所示，i与i-1相连，另一种呢是如图（b），i与i-1不相连。

根据双调旅程，我们知道结点n一定与n相连，那么，如果我们求的dp[n][n-1]，只需将其加上d[n-1][n]就是最短双调闭合路线。

根据上图，很容易写出方程式：

dp[i][j]=dp[i-1][j]+d[i][i-1];

dp[i][i-1]=min(dp[i][i-1],dp[i-1][j]+d[j][i]);

下面是代码实现：

#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
const int maxn = 1010;
int dp[maxn][maxn];
int d[maxn][maxn];
struct point
{int x, y;
}a[maxn];int dis(int i, int j)                   //计算两点之间的距离
{int p,q;if(a[i].y>a[j].y)q=(360+a[j].y-a[i].y)%360;elseq=(360+a[i].y-a[j].y)%360;p=abs(a[i].y-a[j].y)>q?q:abs(a[i].y-a[j].y);                     //求出小弧的长度return (abs(a[i].x-a[j].x)*400+p);                  //距离=两点的轨道差*400+两点的扇区差
}
int main()
{int t,n;scanf("%d",&t);while(t-- ){scanf("%d", &n);a[1].x=0;a[1].y=0;                                      //把起点（0，0）加上for(int i = 2; i <= n+1; i++)scanf("%d %d", &a[i].x, &a[i].y);for(int i = 1; i <= n+1; i++){for(int j = 1; j <= n+1; j++){d[i][j] = dis(i, j);               //d[i][j]为i点到j点的距离}}dp[1][2] = d[1][2];                 for(int i = 3; i <= n+1; i++){for(int j = 1; j < i-1; j++){dp[j][i] = dp[j][i-1] + d[i-1][i];                /*      dp[j][i]为j点到1点，再从1点到i点的距离，这一步是为下一循环求dp[i][i+1]做准备，其实就是图a      */}dp[i-1][i] = 999999999;for(int j = 1; j < i-1; j++){int sum = dp[j][i-1] + d[j][i];if(dp[i-1][i] > sum)dp[i-1][i] = sum;                         /*     dp[i-1][i]为i-1点到1点，再从1点到i点的最短距离,这个距离只要加上边d[i-1][i]就是从1点到i点的最短闭合旅程，其实就是图b      */      }}dp[n+1][n+1] = dp[n][n+1] + d[n][n+1];printf("%d\n", dp[n+1][n+1]+10*n);        /*   dp[n+1][n+1]就是最终的最短闭合旅程，n+1点到1点，再从1点到n+1点的最短距离 ,10*n为读取点中数据的时间 */}return 0;
}

这篇关于百度之星资格赛——Disk Schedule（双调旅行商问题）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！