模电·基本共集放大电路

本文主要是介绍模电·基本共集放大电路，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

基本共集放大电路

一、电路的组成
二、静态分析
三、动态分析

一、电路的组成

根据放大电路的组成原则，晶体管应工作在放大区，即 ${\large u\tiny BE}>{U\tiny on}$ ， ${\large u\tiny CE}≥{\large u\tiny BE}$ ，所以在下图1.基本共集放大电路所示电路中，晶体管的输入回路加基极电源 $V\tiny BB$ ，它与 $R\tiny b$ 、 $R\tiny e$ 共同确定合适的基极静态电流；晶体管的输出回路加集电极电源 $V\tiny CC$ ，它提供集电极电流和输出电流。画出图（a）所示电路的直流通路如图（b）所示，电源 $V\tiny BB$ 和 $V\tiny CC$ 的负端接地；交流通路如图（c）所示，集电极是输入回路和输出回路的公共端。
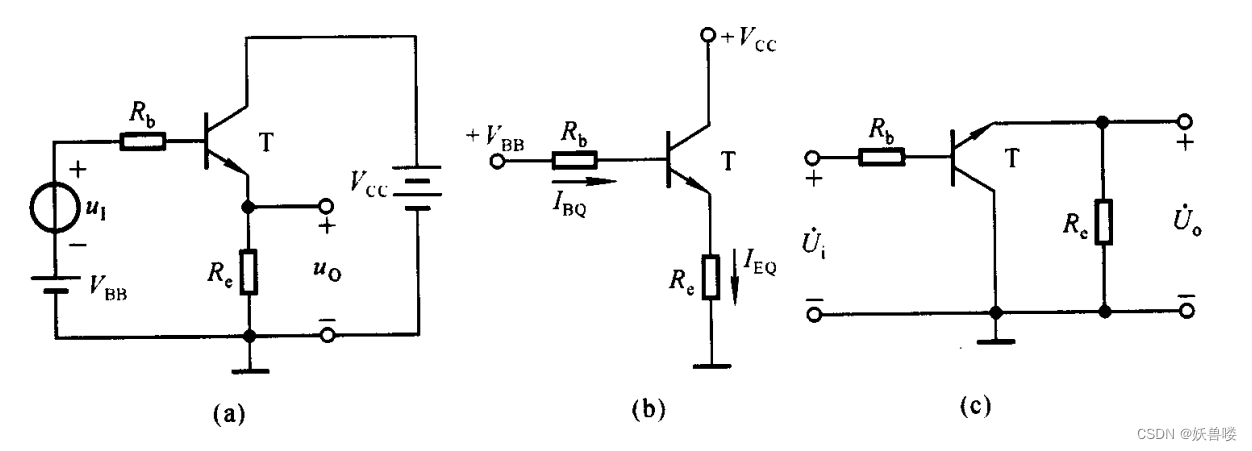
在这里插入图片描述

图1. 基本共集放大电路 （a）电路（b）直流通路（c）交流通路

交流信号 $u\tiny i$ 输入时，产生动态的基极电流 ${i\tiny b}$ ，驮载在静态电流 $I\tiny BQ$ 之上，通过晶体管得到放大了的发射极电流 $\large i\tiny E$ ，其交流分量 $\large i\tiny e$ 在发射极电阻 $R\tiny e$ 上产生的交流电压即为输出电压 $u\tiny o$ 。由于输出电压由发射极获得，故也称共集放大电路为射极输出器具。

二、静态分析

在图1.（b）所示直流通路中，列出输入回路的方程
${V\tiny BB}={I\tiny BQ}{R\tiny b}+{U\tiny BEQ}+{I\tiny EQ}{R\tiny e}={I\tiny BQ}{R\tiny b}+{U\tiny BEQ}+(1+\beta){I\tiny BQ}{R\tiny e}$
便得到基极静态电流 $I\tiny BQ$ 、发射极静态电流 $I\tiny EQ$ 和管压降 ${U\tiny CEQ}$
$\begin{cases} {I\tiny BQ}=\frac{{V\tiny BB}-{U\tiny BEQ}}{{R\tiny b}+(1+\beta){R\tiny e}}\\ \\ {I\tiny EQ}=(1+\beta){I\tiny BQ}\\ \\ {U\tiny CEQ}={V\tiny CC}-{I\tiny EQ}{R\tiny e} \end{cases}$

三、动态分析

把图1.（c）所示电路中的晶体管用其 $h$ 参数等效模型取代便得到共集放大电路的交流等效电路，如图2.所示。
在这里插入图片描述

图2. 基本共集放大电路的交流等效电路

根据电压放大倍数的定义，利用 $\.I\tiny b$ 对 $\.I\tiny c$ 的控制关系，可得出 $\.A\tiny u$ 的表达式为
${\.A\tiny u}=\frac{\.U\tiny o}{\.U\tiny i}=\frac{{I\tiny e}{R\tiny e}}{{I\tiny b}({R\tiny b}+{\large r\tiny be})+{I\tiny e}{R\tiny e}}=\frac{(1+\beta){I\tiny b}{R\tiny e}}{({R\tiny b}+{\large r\tiny be}){I\tiny b}+(1+\beta){I\tiny b}{R\tiny e}}$ ${\.A\tiny u}=\frac{(1+\beta){R\tiny e}}{{R\tiny b}+{\large r\tiny be}+(1+\beta){R\tiny e}}$
${\.A\tiny u}=\frac{(1+\beta){R\tiny e}}{{R\tiny b}+{\large r\tiny be}+(1+\beta){R\tiny e}}$ 表明， $\.A\tiny u$ 大于0且小于1，即 $\.U\tiny o$ 与 $\.U\tiny i$ 同相且 ${U\tiny o}<{U\tiny i}$ 。当 $(1+\beta){R\tiny e}>>{R\tiny b}+{\small r\tiny be}$ 时， ${\.A\tiny u}≈1$ ，即 ${\.U\tiny o}≈{\.U\tiny i}$ ，故常称共集放大电路为射极跟随器。虽然 $|{\.A\tiny u}|<1$ ，电路无电压放大能力，但是输出电流 $I\tiny e$ 远大于输入电流 $I\tiny b$ ，所以电路仍有功率放大作用。
根据输入电阻 $R\tiny i$ 的物理意义能够得出输入电阻 $R\tiny i$ 表达式
${R\tiny i}=\frac{\.U\tiny i}{\.I\tiny i}=\frac{\.U\tiny i}{\.I\tiny b}=\frac{{\.I\tiny b}({R\tiny b}+{\large r \tiny be})+{\.I\tiny e}{R\tiny e}}{\.I\tiny b}$ ${R\tiny i}={R\tiny b}+{\large r\tiny be}+(1+\beta){R\tiny e}$
可见，发射极电阻 $R\tiny e$ 等效到基极回路时，将增大到 $(1+\beta)$ 倍，因此共集放大电路的输入电阻比共射放大电路的输入电阻大得多，可达几十千欧到几百千欧。
为了计算输出电阻 $R\tiny o$ ，令输入信号为零，在输出端加正弦波电压 $U\tiny o$ 求出因其产生的电流 $I\tiny o$ ，则输出电阻 ${R\tiny o}=\frac{U\tiny o}{I\tiny o}$ ，如图3.所示。
在这里插入图片描述

图3. 基本共集放大电路输出电阻求解
在图中，

I\tiny o

由两部分组成，一部分是

U\tiny o

在

R\tiny e

上产生的电流

{\large I}{\tiny Re}

，另一部分是

U\tiny o

由于作用于晶体管的基极回路产生基极电流

I\tiny b

从而获得的

I\tiny e

，它们分别为

{I\tiny b}=\frac{U\tiny o}{{R\tiny o}+{\large r\tiny be}}，{I\tiny e}=(1+\beta)\frac{U\tiny o}{{R\tiny b}+{\large r\tiny be}}

{I\tiny o}={\large I\tiny Re}+{I\tiny e}

所以，输出电阻的表达式为

{R\tiny o}=\frac{U\tiny o}{I\tiny o}=\frac{U\tiny o}{\frac{U\tiny o}{R\tiny e}+(1+\beta)\frac{U\tiny o}{{\small R\tiny b}+{\large r\tiny be}}}=\frac{1}{\frac{1}{R\tiny e}+(1+\beta)\frac{1}{{\small R\tiny b}+{\large r\tiny be}}}

故

{R\tiny o}={R\tiny e}//\frac{{R\tiny b}+{\large r\tiny be}}{1+\beta}

可见，基极回路电阻

R\tiny b

等效到射极回路时，应减小到原来的

\frac{1}{1+\beta}

。由于通常情况下，

R\tiny e

取值较小，

\large r\tiny be

也多在几百欧到几千欧，而

\beta

至少几十倍，所以

R\tiny o

可小到几十欧。
因为共集放大电路输入电阻大、输出电阻小，因而从信号源索取的电流小而且带负载能力强，所以常用于多级放大电路的输入级和输出级;也可用它连接两电路，减少电路间直接相连所带来的影响，起缓冲作用，

【例】图1.（a）所示电路中，已知 ${V\tiny BB}=6V$ ， ${V\tiny CC}=12V$ ， ${R\tiny b}=15kΩ$ ， ${R\tiny e}=5kΩ$ ；晶体管的 ${U\tiny BEQ}=0.7V$ ， ${\large r\tiny bb'}=200Ω$ ， $\beta =150$ 。试估算Q点、 $\.A\tiny u$ 、 $R\tiny i$ 和 $R\tiny o$ 。
解：根据
$\begin{cases} {I\tiny BQ}=\frac{{V\tiny BB}-{U\tiny BEQ}}{{R\tiny b}+(1+\beta){R\tiny e}}\\ \\ {I\tiny EQ}=(1+\beta){I\tiny BQ}\\ \\ {U\tiny CEQ}={V\tiny CC}-{I\tiny EQ}{R\tiny e} \end{cases}$ 可得
$\begin{cases} {I\tiny BQ}=\frac{{6}-{0.7}}{{15}+(1+150){*5}}=0.00688mA=6.88μA\\ \\ {I\tiny EQ}=(1+150){*0.00688}=1.04mA\\ \\ {U\tiny CEQ}={12}-{1.04}{*5}=6.8V \end{cases}$
${\large r\tiny be}≈{\large r\tiny bb'}+\beta\frac{U\tiny T}{I\tiny CQ}≈(200+150*\frac{26}{1})Ω=4100Ω=4.1kΩ$
所以
${\.A\tiny u}=\frac{(1+\beta){R\tiny e}}{{R\tiny b}+{\large r\tiny be}+(1+\beta){R\tiny e}}=\frac{(1+150){*5}}{{15}+{4.1}+(1+150){*5}}≈0.975$
${R\tiny i}={R\tiny b}+{\large r\tiny be}+(1+\beta){R\tiny e}=(15+4.1+151*5)kΩ≈774kΩ$
${R\tiny o}={R\tiny e}//\frac{{R\tiny b}+{\large r\tiny be}}{1+\beta}≈\frac{{R\tiny b}+{\large r\tiny be}}{1+\beta}=(\frac{15+4.1}{1+150}*{10^3})Ω≈126Ω$