本文主要是介绍校招选择题汇总【树(2)】含答案解析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.在一非空二叉树的中序遍历序列中,根结点的右边(A)
A.只有右子树上的所有结点
B.只有右子树上的部分结点
C.只有左子树上的部分结点
D.只有左子树上的所有结点
解析:中序遍历:左根右
2.深度为5的二叉树至多有(D)个结点
A.16
B.10
C.32
D.31
解析:2的k次方减一,k=5,代入得31
3.红黑树中已经有n个数据,寻找某个key是否存在的时间复杂度为(A)
A.o(logn)
B.o(n)
C.o(n二次方)
D.o(1)
解析:红黑树是平衡二叉树,也就是左右子树是平衡的,高度大概相等。
这种情况等价于一块完全二叉树的高度,查找的时间复杂度是树的高度,为logn
4.某二叉树的先序遍历是12453,中序遍历是42513,那么其后续遍历是?(A)
A.45231
B.42351
C.12345
D.54321
解析:

5.一棵深度为4的三叉树,最多有多少个节点?(B)
A.24
B.40
C.36
D.54
解析:层数从1到4分别为:1,3,9,27,所以总和40
6.n个节点的二叉树,最多可以有多少层?(D)
A.n/2
B.log(n)
C.n-1
D.n
解析:最多n层,每层1个,最少log2(n+1),每层填满
7.对n(n≥2)个权值均不相同的字符构成哈夫曼树, 下列关于该哈弗曼树的叙述中,错误的是(A)
A.该树一定是一棵完全二叉树
B.树中一定没有度为1的结点
C.树中两个权值最小的结点一定是兄弟结点
D.树中任一非叶结点的权值一定不小于下一层任一结点的权值
解析:哈夫曼树也叫最右二叉树和带权路径最小树,是一颗二叉树,但并不一定是完全的二叉树
结点的孩子个数称为结点的度,哈夫曼树中只有度为2的结点和度为0的叶子结点
哈夫曼树的构造是从底到上,从小到大,所以最小权值的两个结点一定用于底部,是兄弟结点
根据哈弗曼树的定义,一棵二叉树要使其WPL值最小,必须使权值越大的叶子结点越靠近根结点,而权值越小的叶子结点
越远离根结点,任一非叶子结点的权值是等于其自己孩子结点权值之和,大于或等于下一层的任一结点的权值
8.若把堆看成是一棵完全二叉树,则该树一定是一棵二叉排序树(B)
A.对
B.错
解析:堆对于左右子树的大小关系没有要求,而二叉排序树有要求。
9.在下述论述中,正确的是(D)
①只有一个结点的二叉树的度为 0 ;
②二叉树的度为 2 ;
③二叉树的左右子树可任意交换;
④深度为 K 的顺序二叉树的结点个数小于或等于深度相同的满二叉树。
A.①②③
B.②③④
C.②④
D.①④
解析:二叉树最大的度为2,可以小于2
10.对于下列关键字序列,不可能构成某二叉排序树中一条查找路径的序列是(A)
A.95, 22, 91, 24, 94, 71
B.92, 20, 91, 34, 88, 35
C.21, 89, 77, 29, 36, 38
D.12, 25, 71, 68, 33, 34
解析:前面的节点,或者比后面的节点都大,或者比后面的节点都小。
例如 95, 22, 91, 24, 94, 71。
95比 22, 91, 24, 94, 71都大
22比91, 24, 94, 71 都小
91 比 24, 94, 71都大 (不符合,91比94小)
24 比 94, 71都 小
94 比 71大
11.已知一棵二叉树前序遍历和中序遍历分别为ABDEGCFH和DBGEACHF,则该二叉树的后序遍历为多少?(B)
A.DGEBFHAC
B.DGEBHFCA
C.DEGHBFCA
D.DEGBHACF
解析:前序遍历确定根节点,中序遍历确定左右子树。
A, (BDEG,CFH)
(B,(D,EG));(C,( ,FH))
(E,(G ,)); (F,(H,))
12.由带权为9、2、5、7的四个叶子结点构造一棵哈夫曼树,该树的带权路径长度为(D)
A.23
B.37
C.46
D.44
解析:9*1+7*2+5*3+2*3=44
13.平衡二叉树中,若某个结点的左、右孩子的平衡因子为零,则该结点的平衡因子一定是零(B)
A.对
B.错
解析:
A
B C
D E
对于这颗平衡二叉树,结点A的左右孩子平衡因子都是0,但是A的平衡因子为1。
14.在二叉排序树(二叉搜索树)中,最小值结点的(A)
A.左孩子一定为空指针
B.右孩子一定为空指针
C.左、右指针均为空
D.左、右指针均不为空
解析:二叉排序树: 左 < 中 < 大
5
4 7
2
3
看,这棵树的最小值节点应该是2, 但是2的右子树为3, 大于2, 符合二叉排序树规则,所以2的右子树的指针不一定为空哦
15.某二叉树结点的中序序列为BDAECF,后序序列为DBEFCA,则该二叉树对应的森林包括(C)棵树
A.1
B.2
C.3
D.4
解析:3颗树,如图。二叉树到森林的转换是:二叉树中节点的左孩子是森林中该节点的孩子,右孩子是森林中该节点的兄弟

16.设一棵m叉树中度数为0的结点数为N0 ,度数为1的结点数为Nl ,……,度数为m的结点数为Nm,则N0=(B)
A.Nl+N2+……+Nm
B.l+N2+2N3+3N4+……+(m-1)Nm
C.N2+2N3+3N4+……+(m-1)Nm
D.2Nl+3N2+……+(m+1)Nm
解析:
m叉树总的指针数为N1 + 2N2 + ...+mNm
总的节点数为N 0 +N1 + N2 + ...+Nm ,需要的指针数为N 0 +N1 + N2 + ...+Nm -1
以上两式相等得出N 0 =1+ N2 + 2N3...+(m-1)Nm
17.由3个结点可以构造出多少种不同的有向树?(A)
A.2
B.3
C.4
D.5
解析:有向树的概念是恰有一个顶点入度为0,其余顶点入度为1,那么如果不区分节点和左右树,答案为A
18.有以下5个叶子节点1,1,3,2,5构成的哈夫曼树的带权路径长度为(D)
A.24
B.26
C.23
D.25
解析:
- 结点带权路径长度=该结点到根的路径长度×该结点权
- 哈夫曼树:给定叶子权值和叶子数 可以构造出不同结构的二叉树 其中带权路径长度最小的二叉树称为最优二叉树 哈夫曼树是一种最优二叉树
哈夫曼树算法
- 根据n个权值构造具有n棵二叉树的森林---森林中的每颗二叉树都只有一个根结点 结点的数据域为一个权值 该结点左右子树都是空
- 在森林中选出2棵根结点权值最小的树A B(这样的树不止2棵---任选2棵)---创建一个新结点作为A B的根结点 A B分别作为根结点的左右孩子(权值小的在左边大的在右边 这样规定 哈夫曼树就唯一了)---将A B的权值相加作为根结点的权值---森林中产生一颗新树C(:~有左右孩子各1)
- 在森林中继续选出2棵根结点权值最小的树(2.中产生的C也在选择范围内)---重复2.的过程 直到将森林中所有的数合并成一颗二叉树---这颗二叉树就是哈夫曼树
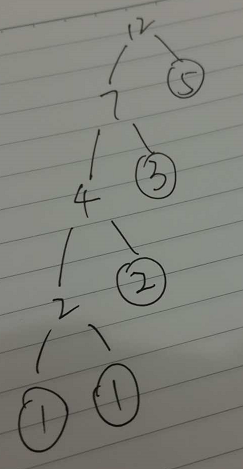
按照上述算法可以得到如下哈夫曼树 其带权路径长度= 5*1+3*2+2*3+(1+1)*4 =25 选D
19.哈夫曼树的结点个数不能是偶数(A)
A.对
B.错
解析:
哈夫曼树只有度为0和2的节点。
假设度为0的节点为N,则度为2的节点为N-1;则节点个数为2N-1,始终为奇数
20.已知某二叉树的后序遍历序列是dabec,中序遍历序列是deabc,它的前序遍历序列是什么?(A)
A.cedba
B.cedab
C.ecdba
D.不能推测出
解析:
由后序序列和中序序列可以唯一确定一棵二叉树,这是由两种遍历序列的特点所决定的。
后序序列的最后一个节点是根节点,中序序列中根节点将序列分为左右子树的中序序列;在后序序列中找到左右子树的序列,其最后一个节点是左右子树的根节点,如此递归就能确定整个二叉树的形态。
其算法实现步骤如下:
- 根据后序序列确定树的根节点
- 根据根节点在中序序列中划分出二叉树的左、右子树包含哪些节点。然后根据左右子树节点在后序序列中的次序可以确定子树的根节点,即回到步骤 1.
- 如此重复上述步骤,知道每棵子树仅有一个节点为止,如下图所示。

21.一棵完全二叉树上有1001个结点,其中叶结点的个数是(E)
A.250
B.500
C.254
D.505
E.以上答案都不对
解析:
完全二叉树的最后一个结点的编号一定是1001,则它的父结点的编号为1001/2=500,则叶子结点个数为1001-500=501.
总结一下:完全二叉树的最后一个结点的编号是n,则它的父结点的编号为[n/2],则叶子结点个数为n-[n/2]。
22.已知 10 个元素 (54,28,16,34,,73,62,95,60,26,43) ,按照依次插入的方法生成一棵二叉排序树,查找值为 62 的结点所需比较次数为(B)
A.4
B.3
C.2
D.5
解析:
依次插入将带插入值直接放入二叉搜索树符合条件位置,使得整棵树左子树均比根小,右子树均比根大,结果如图所示
查找62需要比较3次,分别是和52、73、62比较

23.设一课完全二叉树共有999个结点,则在该二叉树中的叶节点个数是?(B)
A.499
B.500
C.501
D.不唯一
解析:其实完全二叉树有这个性质,最后一个节点/2就得到他的父节点了,而此时的父节点必然是最后一个父节点,也就是说他之后的结点都是叶子节点了所以叶子节点为,999-999/2 = 500.要懂得运用性质,不然题目的完全二叉树是干啥的。
24.下列关于最小生成树的说法中,正确的是(A)
Ⅰ.最小生成树的代价唯一
Ⅱ.所有权值最小的边一定会出现在所有的最小生成树中
Ⅲ.使用普里姆( Prim)算法从不同顶点开始得到的最小生成树一定相同
Ⅳ.使用普里姆算法和克鲁斯卡尔( Kruskal)算法得到的最小生成树总不相同
A.仅Ⅰ
B.仅Ⅱ
C.仅Ⅰ、 Ⅲ
D.仅Ⅱ、 Ⅳ
解析:A、既然是最小生成树,那么代价一定是唯一确定的最小值,但是树形可能不一样
B、设想所有边权值都相同,那么当边数>顶点数-1时,自然有某些边不会出现在最小生成树里
C、情况如B
D、不一定,情况如B
25.现有一棵无重复关键字的平衡二叉树(AVL树),对其进行中序遍历可得到一个降序序列。下列关于该平衡二叉树的叙述中,正确的是(D)
A.根结点的度一定为 2
B.树中最小元素一定是叶结点
C.最后插入的元素一定是叶结点
D.树中最大元素一定是无左子树
解析:只有两个结 点 的平衡二叉树的 根 结点的度 为 1 , A 错误。 中序遍历 后可以得到一个降序序列 ,树中最小元素一定无左子树 (可能有右子树),因此不一定是叶结点, B 错误。最后插入的结点可能会导致 平衡 调整,而不一定是叶结 点 , C 错误
26.不含任何结点的空树(B)
A.是一棵树
B.是一棵二叉树
C.是一棵树也是一棵二叉树
D.既不是树也不是二叉树
解析:二叉树可以为空,但树不可以为空,树是图的特例,图是不能为空的
27.现有一棵无重复关键字的平衡二叉树(AVL树),对其进行中序遍历可得到一个降序序列。下列关于该平衡二叉树的叙述中,正确的是(D)
A.根结点的度一定为2
B.树中最小元素一定是叶结点
C.最后插入的元素一定是叶结点
D.树中最大元素一定是无左子树
解析:只有两个结点的平衡二叉树的根结点的度为1,A错误。中序遍历后可以得到一个降序序列,树中最大元素一定无左子树(可能有右子树),因此不一定是叶结点,B错误。最后插入的结点可能会导致平衡调整,而不一定是叶结点,C错误。
28.已知二叉树Node定义如下, 现在需要设计一个方法交换左子树和右子树, 下列方法中, 可以实现交换的是?(D)
class Node {
public:
Node* left;
Node* right;
char content;
Node(char content);
private:
Node(const Node&);
Node& operator=(const Node& node);
};
A.void swap(Node root) {Node* temp=root.left;root.left=root.right;root.right=temp;}
B.void swap(Node& left, Node& right) {Node temp=left; left=right;right=temp;}
C.void swap(Node* left, Node* right) {Node* temp=left; left=right;right=temp;}
D.void swap(Node*& left, Node*& right) {Node* temp=left; left=right;right=temp;}
解析:
A 传入值显然不能更改
B 传入虽然是指针,但是能透过指针去修改值,指针本身指向的地址也相当于拷贝复制。
C 上同。
D 二级指针概念。
29.一颗完全二叉树第六层有8个叶结点(根为第一层),则结点个数最多有(D)个
A.39
B.72
C.104
D.111
解析:
二叉树第k层最多有2的(k-1)次方个节点
第六层最多有32个节点
第五层最多有16个节点
第四层最多有8个节点
第三层最多有4个节点
第二层最多有2个节点
第一层最多有1个节点
完全二叉树的叶节点只可能出现在后两层
如果完全二叉树有6层,则前5层是满二叉树,总节点数目为16+8+4+2+1+8=39
如果完全二叉树有7层,则前6层是满二叉树,
前六层总节点数目为32+16+8+4+2+1=63
第六层有8个叶子节点,则有32-8=24个非叶子节点
第七层最多有24*2个叶子节点
总节点数目为63+24*2=111
30.在下述几种树中,()可以表示静态查找表(A)
A.次优查找树
B.二叉排序树
C.B-树
D.平衡二叉树
解析:
在有序序列的查找中,如果各个元素的查找概率都是一样的,那么二分查找是最快的查找算法,但是如果查找元素的查找概率是不一样的,那么用二分查找就不一定是最快的查找方法了,可以通过计算ASL来得知。
所以基于这种查找元素概率不想等的有序序列,可以通过构造最优二叉树的方法,使得该二叉树的带权路径长度最小,这样的二叉树的构造代价是非常大的,所以用一种近似的算法,构造次优查找树,该树的带权路径长度近似达到最小。
这篇关于校招选择题汇总【树(2)】含答案解析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








