本文主要是介绍蓝桥杯-路径之谜,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目描述
小明冒充X星球的骑士,进入了一个奇怪的城堡。城堡里面什么都没有,只有方形石头铺成的地面。
假设城堡的地面时n*n个方格。如下图所示。
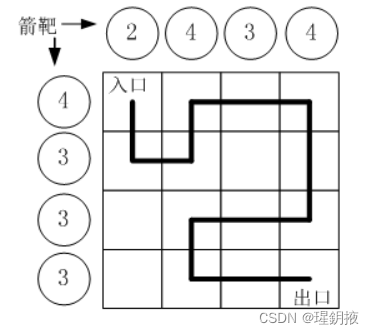
按习俗,骑士要从西北角走到东南角。可以横向或者纵向移动,但是不能斜着走,也不能跳跃。没走到一个新方格,就要向正北方和正西方各射一箭。(城堡的西墙和北墙内各有n个靶子)同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目,你能推断出骑士的行走路线吗?有时是可以的,比如上图中的例子。
本题的要求就是已知箭靶数字,求骑士的行走的路径(测试数据保证路径唯一)。
输入描述
第一行一个整数N(0≤N≤20),表示地面有N*N个方格。
第二行N个整数,空格分开,表示北边的箭靶上的数字(自西向东)
第二行N个整数,空格分开,表示西边的箭靶上的数字(自北向南)
输出描述
输出一行若干个整数,表示骑士路径。
为了方便表示,我们约定每一个小格子用一个数字代表,从西北角开始编号:0,1,2,3…
比如,上图中的方块编号为:
0 1 2 3
4 5 6 7
8 9 10 11
12 13 14 15
样式输入
4
2 4 3 4
4 3 3 3
样例输出
0 4 5 1 2 3 7 11 10 9 13 14 15
题目分析
题目分析:
本题是一个路径推断问题,需要根据已知的箭靶数字来推断骑士在城堡内的行走路径。
首先,我们需要理解题目中的规则和要求。骑士从西北角走到东南角,每次移动到一个新的方格,都需要向正北方和正西方各射一箭。每个方格只能经过一次,且不需要走完所有的方格。
根据输入描述,我们知道第一行输入是整数N,表示地面有NxN个方格。第二行是北边箭靶上的数字,表示自西向东的顺序。第三行是西边箭靶上的数字,表示自北向南的顺序。
输出描述要求我们输出一行若干个整数,表示骑士的路径。编号约定是从西北角开始编号:0, 1, 2, 3…
思路:
为了解决这个问题,我们可以使用回溯法(Backtracking)来搜索所有可能的路径,直到找到符合要求的路径为止。下面是解题思路的步骤:
初始化一个N*N的矩阵,用于记录每个方格是否被访问过。初始时,将所有方格标记为未访问。
从起点(0,0)开始,尝试向下或向右移动,每次移动后更新当前位置,并将对应的方格标记为已访问。
在每次移动后,更新箭靶上的数字,即向正北方和正西方各增加一箭的数量。
如果当前位置是终点(N-1,N-1),则检查箭靶上的数字是否符合要求。如果符合要求,则将当前路径加入结果列表。
如果当前位置不是终点,继续尝试向下或向右移动,重复步骤2-4。
当所有可能的路径都被尝试过后,返回结果列表中的第一个有效路径作为最终答案。
代码
#include <bits/stdc++.h>
using namespace std;
const int N=21;
int row[N],col[N]; // 定义行和列的数组
int n; // 定义矩阵的大小
int dx[]={-1,0,1,0},dy[]={0,-1,0,1}; // 定义四个方向的偏移量
vector<int> path; // 用来存储路径
bool st[N][N]; // 定义状态数组,用于记录每个位置是否已经访问过// 深度优先搜索函数
bool dfs(int x,int y)
{if(x==n-1 && y==n-1) // 如果到达终点{for(int i=0;i<n;i++)if(row[i]!=0 || col[i]!=0) // 如果还有未访问的行或列,返回falsereturn false;return true; // 否则返回true}for(int i=0;i<4;i++) // 遍历四个方向{int a=x+dx[i],b=y+dy[i]; // 计算下一个位置的坐标if(a<0 || a>=n || b<0 || b>=n || st[a][b]) continue; // 如果越界或者已经访问过,跳过if(row[a]<=0 || col[b]<=0) continue; // 如果该位置无法访问,跳过st[a][b]=true; // 标记该位置已访问row[a]--,col[b]--; // 更新行和列的剩余数量path.push_back(a*n+b); // 将该位置加入路径if(dfs(a,b)) return true; // 如果找到一条路径,返回truest[a][b]=false; // 回溯,恢复该位置的状态row[a]++,col[b]++; // 恢复行和列的剩余数量path.pop_back(); // 回溯,将该位置从路径中移除}return false; // 如果四个方向都无法继续前进,返回false
}int main()
{cin>>n; // 输入矩阵的大小for(int i=0;i<n;i++) cin>>col[i]; // 输入列的数量for(int i=0;i<n;i++) cin>>row[i]; // 输入行的数量col[0]--,row[0]--; // 将起点的行列数量减一st[0][0]=true; // 标记起点已访问path.push_back(0); // 将起点加入路径dfs(0,0); // 从起点开始深度优先搜索for(auto x:path) cout<<x<<' '; // 输出路径return 0;
}
这篇关于蓝桥杯-路径之谜的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






