本文主要是介绍带环链表和链表的复制，检验你链表的学习情况，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
前言：带环链表是链表中的经典问题，需要一定的数理思维，一定要掌握其来龙去脉，这样可以加深理解。本文主要讲解一下个人对带环链表的理解。
带环链关的OJ题
1.判断链表是否带环
题目：
141. 环形链表
给你一个链表的头节点
head，判断链表中是否有环。如果链表中有某个节点，可以通过连续跟踪
next指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数pos来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos不作为参数进行传递 。仅仅是为了标识链表的实际情况。如果链表中存在环 ，则返回
true。 否则，返回false。示例 1：
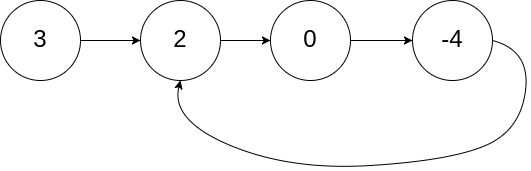
输入：head = [3,2,0,-4], pos = 1 输出：true 解释：链表中有一个环，其尾部连接到第二个节点。示例 2：
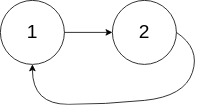
输入：head = [1,2], pos = 0 输出：true 解释：链表中有一个环，其尾部连接到第一个节点。示例 3：
输入：head = [1], pos = -1 输出：false 解释：链表中没有环。提示：
- 链表中节点的数目范围是
[0, 104]-105 <= Node.val <= 105pos为-1或者链表中的一个 有效索引 。
思路：
这题判断链表是否带环，方法这里用的是快慢指针的方法，慢指针走一步，快指针走两步。如果快慢指针可以相遇，那么就说明带环；如果快指针的指向空或指针的下一个节点为空，那么就说明，遍历完链表，就是不带环。带环的链表是走不出循环的。
代码如下：
typedef struct ListNode ListNode;
bool hasCycle(struct ListNode *head) {ListNode* fast = head;//快指针ListNode* slow = head;//慢指针while(fast&&fast->next)//两个条件不能颠倒顺序{slow = slow->next;fast = fast->next->next;if(fast==slow){return true;} }return false;
}为什么fast和slow一定会相遇呢？
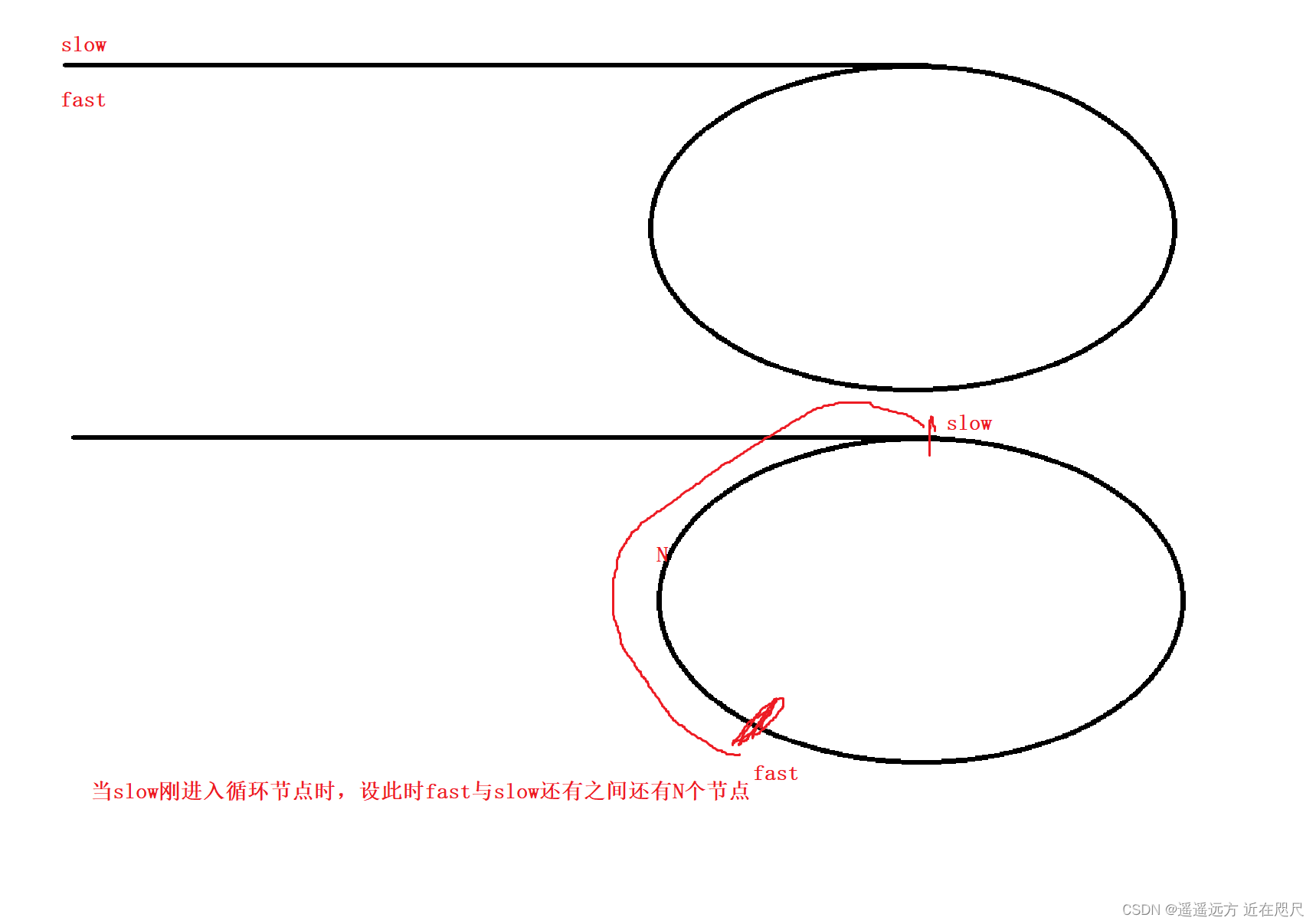此时，是fast追赶slow，他们俩的距离为N，并且fast每次走两步，slow每次走一步，那么每循环一次，fast与slow的距离就会减1，直到两个指针的距离为0.
拓展：
带环链表，如果fast是slow的三倍，两个指针是否会一定相遇？四倍呢？……？
三倍的情况：
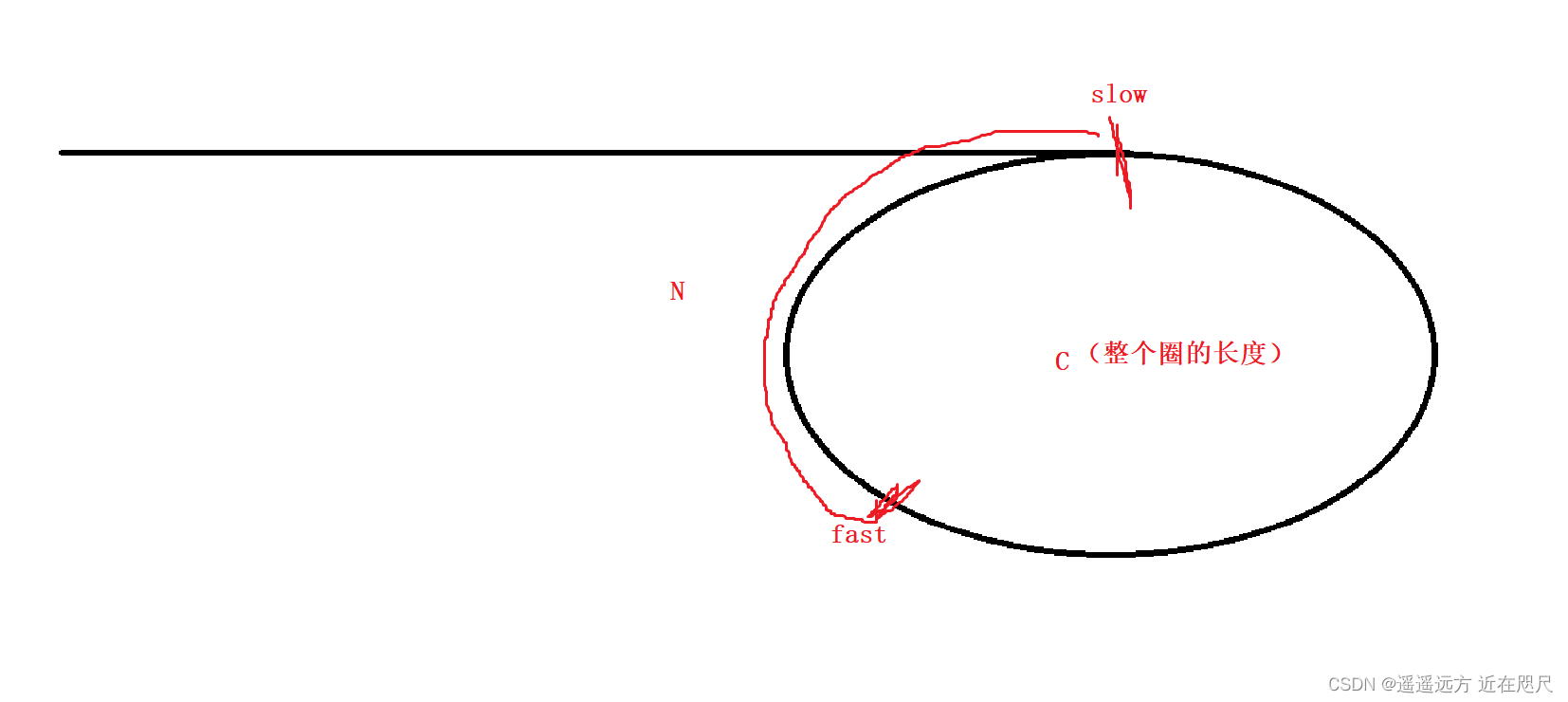
fast一次走三步，slow一次走三步，fast和slow每走一步，他俩的距离就减少2.
如果N为偶数，那么fast和slow一定相遇。
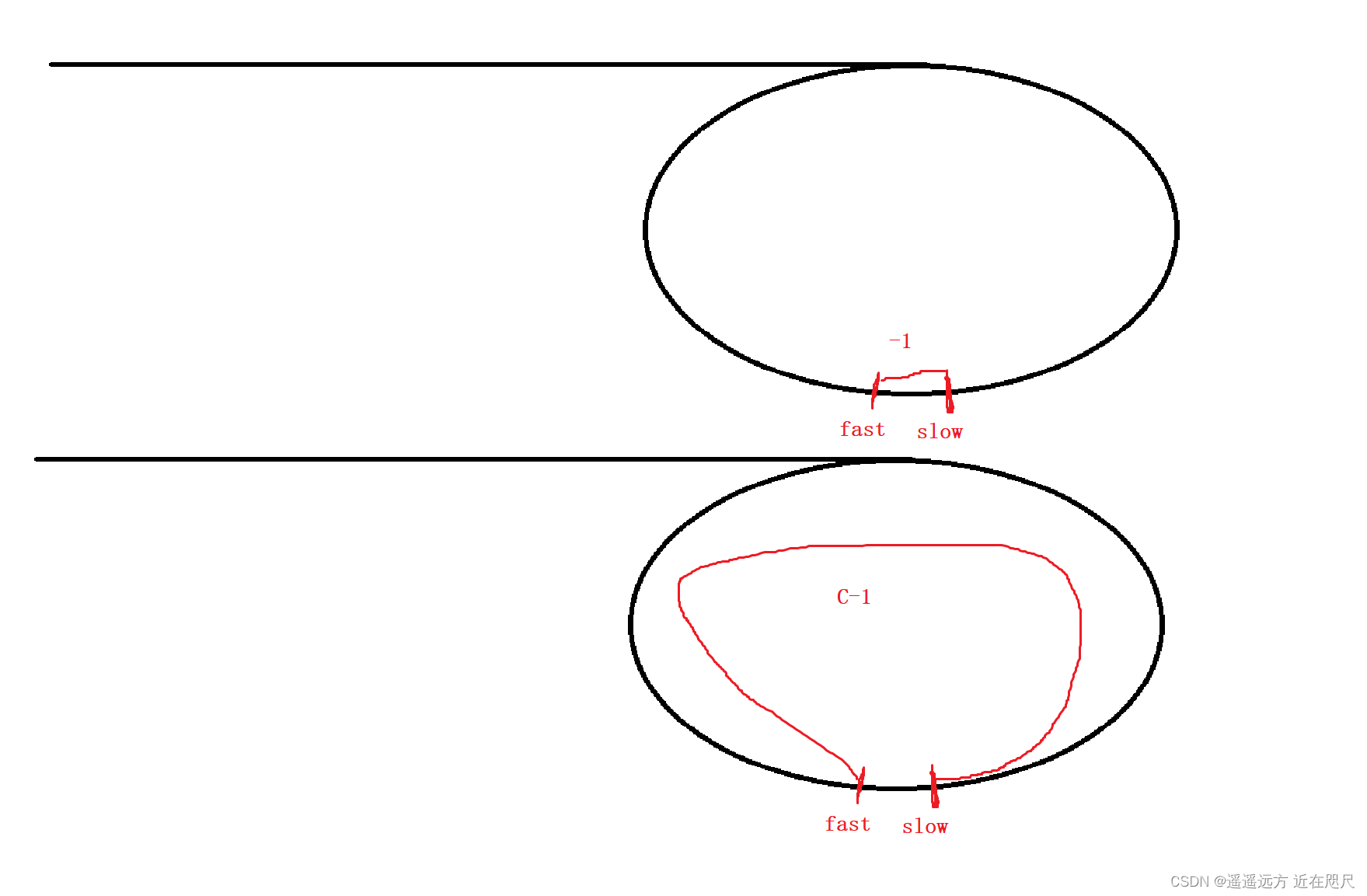
如果N为奇数，那么slow和fast会错过，错过时，slow与fast的距离为-1，设整个圈的长度为C，
此时的-1可以理解为fast与slow的距离为C-1，
如果C-1为偶数，C为奇数那么fast和slow一定可以相遇：
那么C-1为奇数，C为偶数，那么fast和slow不会相遇，那么fast和slow再次错开，并且距离仍为C-1，仍不可能相遇，循环往复，fast和slow就一定不相遇。
但事实上一定不相遇的条件(N为奇数，C为偶数）是否能同时成立呢？
以下是一段证明：
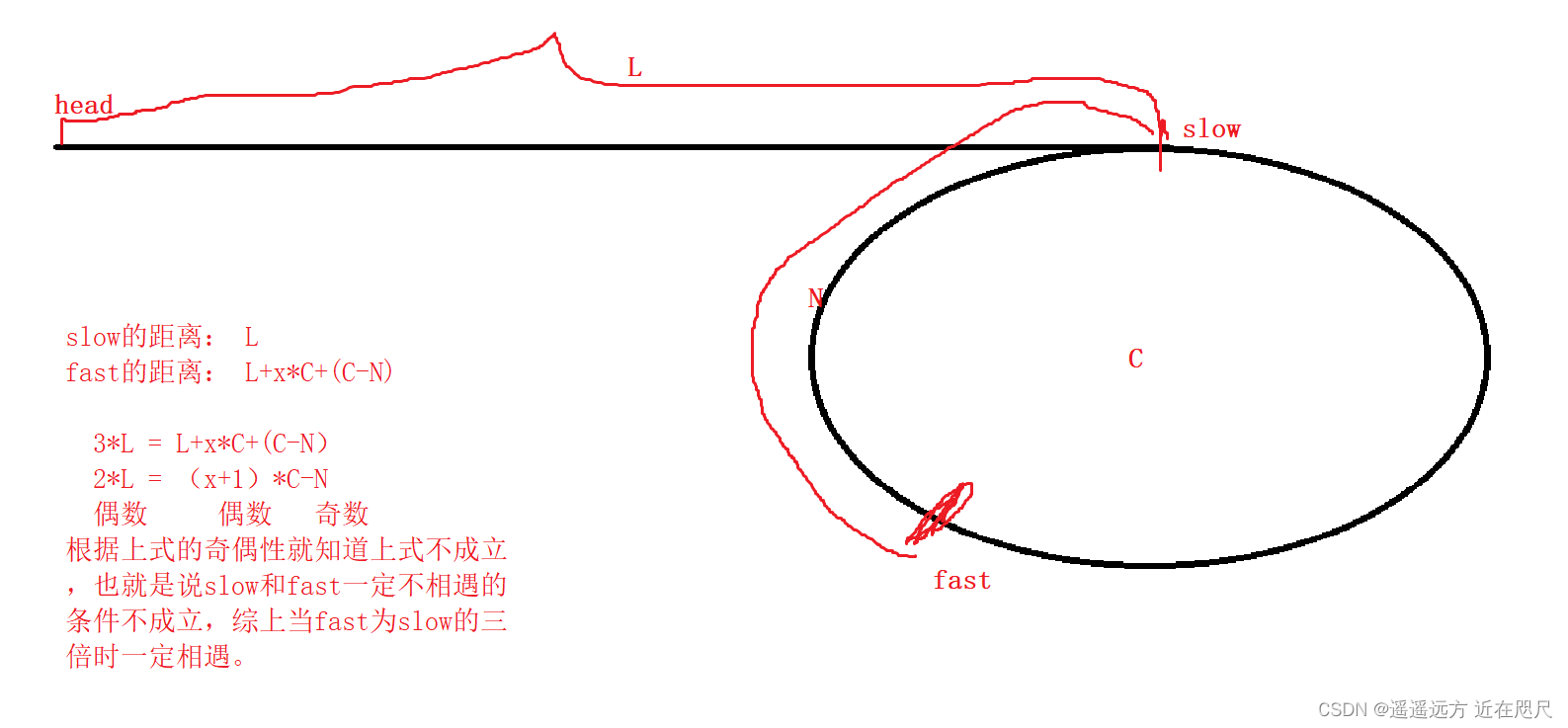
结论：当fast为slow的三倍时，一定相遇。
四倍：
1.如果N为3的倍数，那么一定相遇；
2.如果N%3==1,那么fast与slow错过后两个人的距离为-2，即为C-2，
a.如果（C-2为）%3==0时，一定相遇;
b. 如果（C-2）%3==1时那么一定不相遇；
c.如果（C-2）%3==2时，那么两个错过后的距离为C-1，（C-1）%3==2，之后就是两个的距离一 直为C-1，那么一定不相遇。
3.如果N%3==2,那么fast与slow错过后两个的距离为-1，即为C-1，
a.如果C-1为偶数时，一定相遇;
b.如果（C-1）%3==1，两个人错过后的距离为C-2,（C-2）%3==0
c.如果（C-2）%3==2，两个错过后的距离为C-1，（C-1）%3==1,之后就是（C-1）和（C-2）循 环往复，所以时一定不相遇。
根据以上的讲解可以自己推导其他的几种情况。
2.找带环链表的环的入口
题目：
142. 环形链表 II
给定一个链表的头节点
head，返回链表开始入环的第一个节点。 如果链表无环，则返回null。如果链表中有某个节点，可以通过连续跟踪
next指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数pos来表示链表尾连接到链表中的位置（索引从 0 开始）。如果pos是-1，则在该链表中没有环。注意：pos不作为参数进行传递，仅仅是为了标识链表的实际情况。不允许修改 链表。
示例 1：
输入：head = [3,2,0,-4], pos = 1 输出：返回索引为 1 的链表节点 解释：链表中有一个环，其尾部连接到第二个节点。示例 2：
输入：head = [1,2], pos = 0 输出：返回索引为 0 的链表节点 解释：链表中有一个环，其尾部连接到第一个节点。示例 3：
输入：head = [1], pos = -1 输出：返回 null 解释：链表中没有环。提示：
- 链表中节点的数目范围在范围
[0, 104]内-105 <= Node.val <= 105pos的值为-1或者链表中的一个有效索引
思路1:
通过快慢指针，找到slow与fast相遇的位置，并定义一个新指针为meet，让meet和head同时走一步，直到meet和head相遇，相遇的位置就是环的入口。
代码：
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/
typedef struct ListNode ListNode;
struct ListNode *detectCycle(struct ListNode *head) {ListNode* fast = head;ListNode* slow = head;while(fast&&fast->next){slow = slow->next;fast = fast->next->next;//slow与fast相遇if(slow==fast){ListNode* meet = slow;while(meet!=head){meet = meet->next;head = head->next;}return head;}}return NULL;
}证明为什么meet和head同时走相遇的位置为环入口的位置？
思路2：
将链表转换为相交链表，变成处理相交链表找交点的问题。
相交链表的链接：这个的题解可以找一下我以前的博客：这里就不多讲了，这个题如果以前写过了，直接复制粘贴就可以了，那么这题就会非常好写。
160. 相交链表
代码：
/*** Definition for singly-linked list.* struct ListNode {* int val;* struct ListNode *next;* };*/
typedef struct ListNode ListNode;
//实现找到交叉链表的公共节点
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {ListNode* ptailA = headA;ListNode* ptailB = headB;int lenA = 1;int lenB = 1;while(ptailA){ptailA = ptailA->next;lenA++;}while(ptailB){ptailB = ptailB->next;lenB++;}if(ptailA!=ptailB){return NULL;}//假设法ListNode* listlong = headA;ListNode* listshort = headB;int k = fabs(lenA-lenB);//两个链表长度的差if(lenB>lenA){listlong = headB;listshort = headA;}while(k--){listlong = listlong->next;}while(listlong){if(listlong==listshort){return listlong;}listlong = listlong->next;listshort = listshort->next;}return NULL;
}
struct ListNode *detectCycle(struct ListNode *head) {ListNode* fast = head;ListNode* slow = head;while(fast&&fast->next){slow = slow->next;fast = fast->next->next;if(slow==fast){ListNode* newhead = slow->next;slow->next = NULL; return getIntersectionNode(newhead,head);}}return NULL;
}你链表的试金石：随机链表的复制
题目：
138. 随机链表的复制
给你一个长度为
n的链表，每个节点包含一个额外增加的随机指针random，该指针可以指向链表中的任何节点或空节点。构造这个链表的 深拷贝。解释一下什么是深拷贝：拷贝值和指针指向和当前链表一模一样的链表。 深拷贝应该正好由
n个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的next指针和random指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。例如，如果原链表中有
X和Y两个节点，其中X.random --> Y。那么在复制链表中对应的两个节点x和y，同样有x.random --> y。返回复制链表的头节点。
用一个由
n个节点组成的链表来表示输入/输出中的链表。每个节点用一个[val, random_index]表示：
val：一个表示Node.val的整数。random_index：随机指针指向的节点索引（范围从0到n-1）；如果不指向任何节点，则为null。你的代码 只 接受原链表的头节点
head作为传入参数。示例 1：
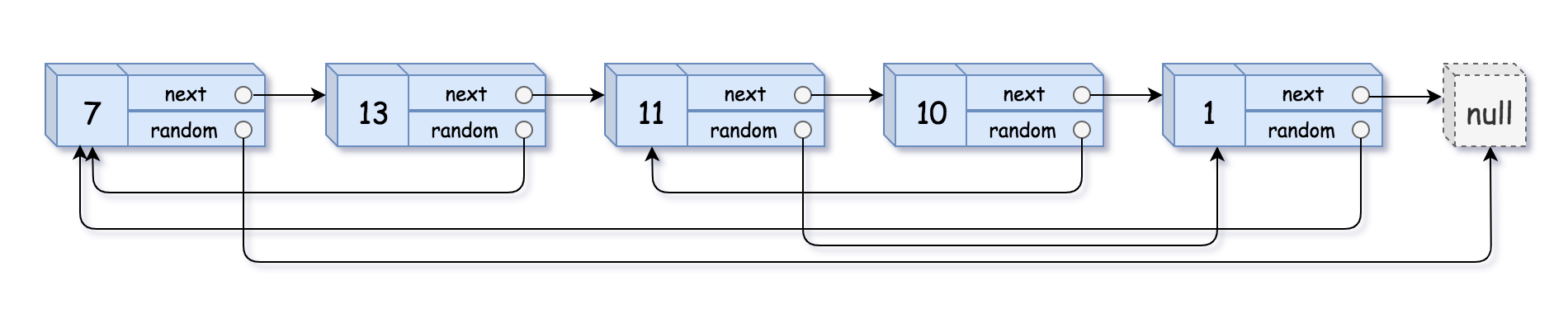
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]] 输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]示例 2：
输入：head = [[1,1],[2,1]] 输出：[[1,1],[2,1]]示例 3：
输入：head = [[3,null],[3,0],[3,null]] 输出：[[3,null],[3,0],[3,null]]提示：
0 <= n <= 1000-104 <= Node.val <= 104Node.random为null或指向链表中的节点。
题目要求的简单说明，除去random复制链表剩余的部分实现很简单，这题的重点主要是新链表random的指向如何和原链表保持一致。就根据现在所学的知识，以下方式相对简单。
思路：
1.拷贝原链表的节点并将其插入相应的原链表的节点的后面，这里的插入相当于链表中的随机插入。
2.处理random，使复制链表的random指向与原链表一致。
3.将现在链表中的复制链表部分尾插到新链表中，并恢复原链表（原链表恢不恢复，都可以，主要根据题目吧，如果题过不来了就恢复，过得了就恢不恢复都可以）
以例三为例用图片演示一下思路：
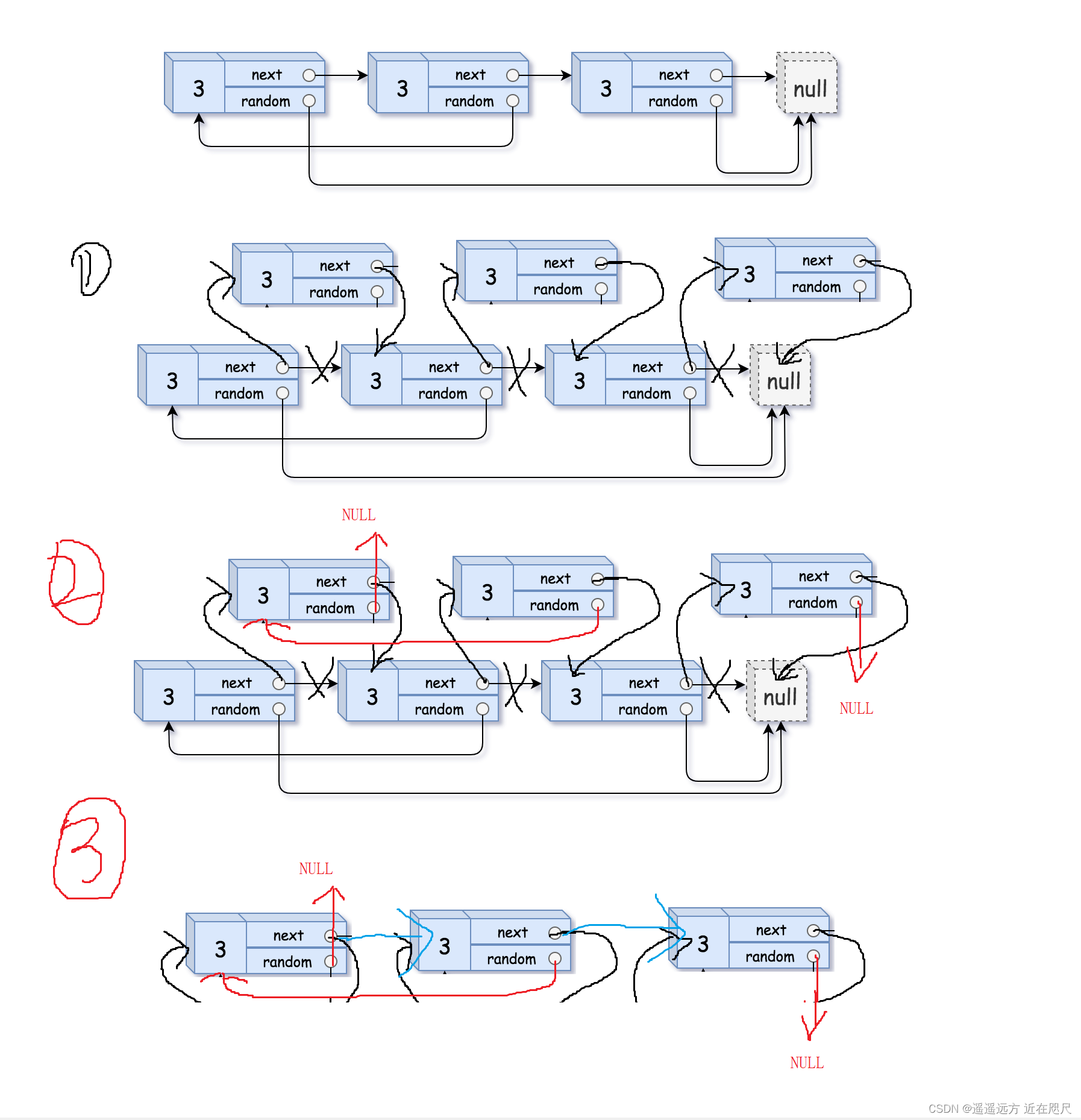
代码：
/*** Definition for a Node.* struct Node {* int val;* struct Node *next;* struct Node *random;* };*/struct Node* copyRandomList(struct Node* head) {struct Node*cur = head;//拷贝原链表并插入相应节点的后面while(cur){struct Node*copy = (struct Node*)malloc(sizeof(struct Node));if(copy==NULL){return NULL;}copy->val = cur->val;//注意以下两句不能交换位置 copy->next = cur->next;cur->next = copy;cur = copy->next;}//处理randomcur = head;while(cur){struct Node* copy = cur->next;//如果原链表的该节点的random指向NULL，那么复制节点的random也指向if(cur->random==NULL){copy->random = NULL;}else{//这一句是整个题的思路的重点：此时链表的结构，每个copy节点的random的指向的位置为前一个节点的random的下一个节点copy->random = cur->random->next;}cur = copy->next;}//尾插并恢复原链表cur = head;struct Node* newhead = NULL,* newtail = NULL;while(cur){struct Node* copy = cur->next;struct Node* next = copy->next;//这里的尾插是没有哨兵位的尾插，需要判断是否为空if(newhead==NULL){newhead = newtail = copy;}else{newtail->next = copy;newtail = newtail->next;}cur->next = next;cur = copy->next;}return newhead;
}
结语：
希望本文章能让您有所收获，您能有所收获就说明我的文章还可以。
这篇关于带环链表和链表的复制，检验你链表的学习情况的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
