【通信原理二】第八章信道及信道编码

本文主要是介绍【通信原理二】第八章信道及信道编码，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在上一章中，我们讨论过信源以及信源编码，本章节介绍了信道以及信道编码，主要介绍信道输入输出的数学关系——信道模型（channel model）以及信道最高能实现的传输速率——信道容量（channel capability）。

一、信道

通信是信息的传输，而通信系统是将信源输出的信息变成信号后进行传输，信道是信号传输的通道。

对于信道，我们可以划分为狭义信道与广义信道。狭义信道也叫物理信道，指物理传输媒介；广义的信道泛指发端和收端之间的一切环节。

同时，也可以划分为恒参信道与随参信道。恒参信道也叫静态信道、时不变信道，指信道的特性（参数）基本不随时间变化；随参信道也叫时变信道，指信道的特性（参数）随时间随机变化，其中很多无线信道属于随参信道。

二、信道模型

1. 信道的物理属性与数学属性

对于信道，存在物理属性与数学属性。物理属性由传输媒介的物理性质确定；而在数学建模中，信道是一个黑箱，它把输入信号映射为输出信号。输入信号以及输出信号的连续或离散，也决定了信道是时间连续信号还是时间离散信道。时间连续信道，也叫波形信道或模拟信道，输入输出是时间连续的波形 $X(t), Y(t)$ ；时间离散信道的输入输出是序列 $\left \{ X_{n} \right \},\left \{ Y_{n} \right \}$

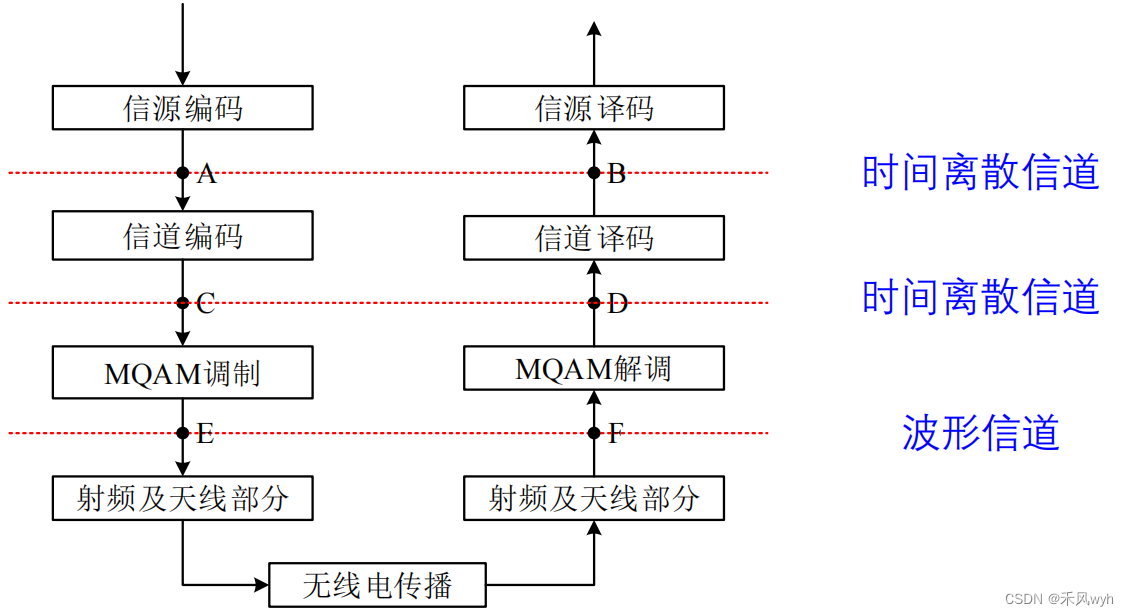
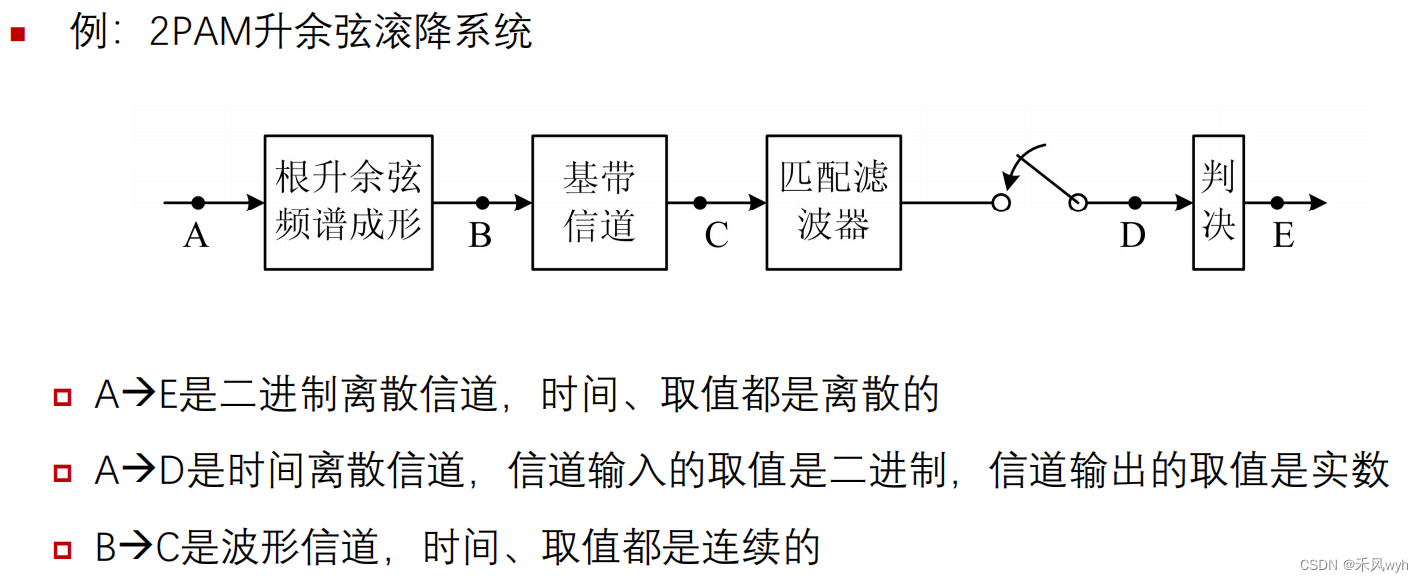
2. 信道建模

之前我们讨论过信道的物理属性和数学属性，根据两者，我们可以将信道建模进行分类——

解析模型和统计模型。解析模型是从物理成因去构建模型；而统计模型是基于数据测量的建模。

对于信道，我们可以分为信道可分为线性信道和非线性信道。之前我们知道波形信道的输入是波形，输出也是波形。波形线性信道如下图所示：（信道连续且线性）

线性信道按是否时变可分为时不变信道和时变信道，同时对应线性时不变系统和线性时变系统。时不变指的是输入推迟，则输出原样推迟；时变指的是对于相同的输入信号，换个时间加到系统输入端后，输出看到的波形不一样。

之前我们知道时间离散信道的输入是序列 $\left \{ x_{n} \right \}$ 为离散的，输出是 $\left \{ y_{n} \right \}$ 也为离散的。我们可以将其分为无记忆信道和有记忆信道。无记忆信道指的是 $\left \{ y_{n} \right \}$ 只与 $\left \{ x_{n} \right \}$ 有关，与其他 $\left \{ x_{k} \right \}, k\neq n$ 无关；有记忆信道指的是输出的每个元素 $\left \{ y_{n} \right \}$ 与序列 $\left \{ x_{n} \right \}$ 的多个元素有关。有记忆信道例如：发送序列到接收端产生了ISI（符号间干扰）的情形。

信道转移概率反应信道的特性，体现输出以及输入之间的关系。时不变指的是表达式与下标t/n无关，无记忆指的是表达式与x的前n项无关。

三、常见信道类型

1. BSC信道：二元对称信道（ Binary symmetric channel，BSC）

BSC信道的输入和输出只有两个取值0、1，并且具有对称的信道转移概率。

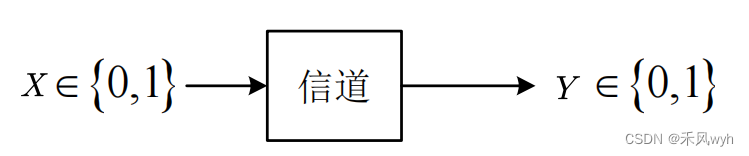
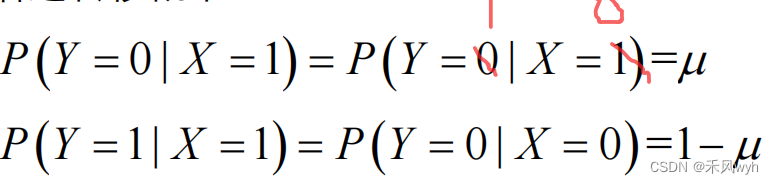
BSC代表这样一种二进制传输系统：每个比特有相同的误比特率，不同比特的比特错误独立，0错为1、1错为0的概率相同

我们知道，信道具有数学属性，BSC的数学逻辑表达为

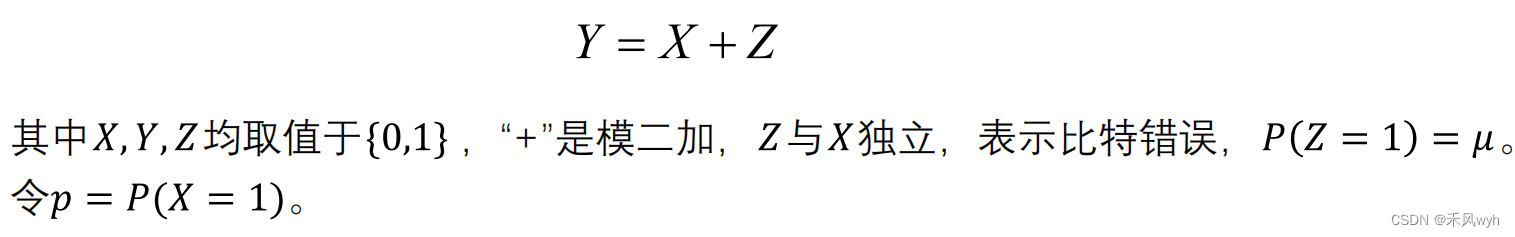
2. BEC信道：二元删除信道（Binary Erasure Channel）

BEC信道与BSC信道类似，不同的是对于错误比特的处理方式，BEC信道的输出Y的取值有三种，0、1、e，出现比特错误输出变为e。

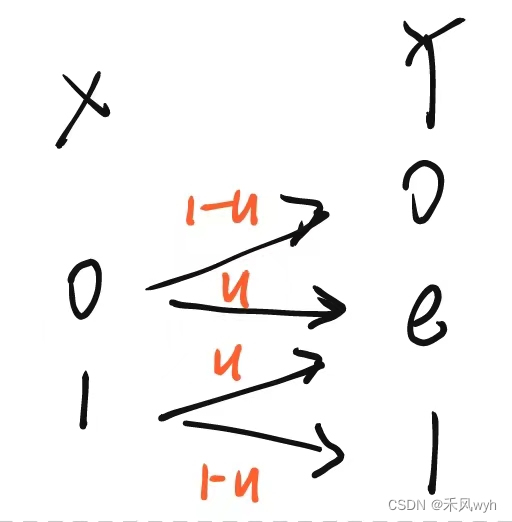
3. 无失真信道

无失真信道分为两种，波形无失真信道以及复包络无失真信道。波形无失真信道不考虑噪声，若信道输出 $y(t)$ 与输入 $x(t)$ 的波形形状相同，只是有延迟和大小差别。表达式为：

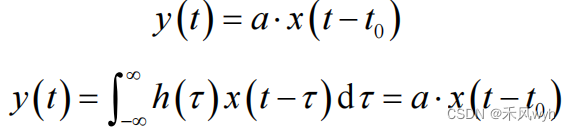
其幅频、相频、时延、群时延为：

复包络无失真信道的输出 $y(t)$ 的复包络 $y_{L}(t)$ 与输入 $x(t)$ 的复包络 $x_{L}(t)$ 波形形状相同，只是有延迟和系数的差别。表达式为：

其幅频、相频、时延、群时延特性为：

总结一下，我们可以得到无失真的条件：

波形无失真：
- 幅频特性是常数
- 相频特性是过原点的直线（时延特性是常数）

复包络无失真：
- 幅频特性是常数
- 相频特性是直线（群时延特性是常数）

4. AWGN信道

AWGN指的是加性白高斯噪声（additive white Gaussian noise），其中高斯是说噪声的电压值是服从高斯分布的随机变量，白是指噪声的带宽非常宽，且功率谱密度是常数。高斯白噪声分为加性高斯白噪声以及理想限带高斯白噪声。下面，我们先讨论加性高斯白噪声：

但是在工程上一般采用的是限带白高斯噪声，下面我们介绍一下理想限带白高斯噪声。在数学上，AWGN是按极限定义的，它是理想限带白噪声的极限。

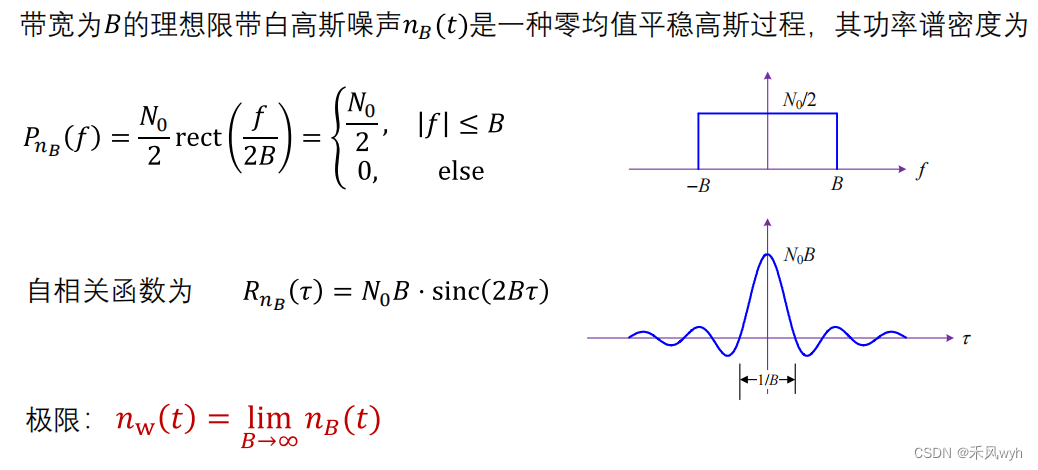
讨论完加性高斯白噪声之后，我们来看一下AWGN信道，AWGN信道分为时间离散的AWGN信道以及时间连续的AWGN信道。信号通过AWGN信道传输时，除了叠加高斯白噪声之外，信号没有任何变化（可以有无失真的幅度系数及时延）表达式为：

$Y(t)=X(t)+n_{w}(t)$ ；

带宽为B, $X(t)$ 的AWGN信道中的带宽是B，噪声是带宽为B的理想限带高斯白噪声表达式为：

$Y(t)=X(t)+n(t)$

信道输出端的信噪比为： $SNR=\frac{\overline{E[X^{2}(t)]}}{N_{0}B}=\frac{S}{\sigma^{2}}$ 。若信号为平稳过程， $SNR=\frac{E[X^{2}(t)]}{N_{0}B}=\frac{S}{\sigma^{2}}$

由于 $Y(t),X(t),n(t)$ 的带宽为B，故可用奈奎斯特采样定理将它们展开为正交级数。令 $T_{s}=\frac{1}{2B}$ ，则有：

$X(t)=\sum_{k=-\infty }^{\infty}X_{k}sinc(\frac{t}{T_{s}}-k)$

$n(t)=\sum_{k=-\infty }^{\infty}n_{k}sinc(\frac{t}{T_{s}}-k)$

$Y(t)=\sum_{k=-\infty }^{\infty}Y_{k}sinc(\frac{t}{T_{s}}-k)$

其中， $Y_{k}=Y(kT_{s}),X_{k}=X(kT_{s}),n_{k}=n(kT_{s})$ ，可以证明 $\left \{ n_{k}\right \}$ 是零均值独立同分布序列，方差为 $\sigma^{2}$ 。此时，时间连续的AWGN信道等价为时间离散的AWGN信道：

$Y_{k}=X_{k}+n_{k}$

下面，我们具体来介绍一下时间离散的AWGN信道。忽略下标，时间离散的AWGN信道的模型为 $Y=X+Z$ ，其中信道输入为 $X$ ，信道输出为 $Y$ ， $Z$ 是零均值高斯噪声， $Z$ 与发送信号 $X$ 独立，其方差为 $\sigma^{2}$ 。Z的概率密度函数为

$p_{Z}(z)=\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{z^{2}}{2\sigma^{2}}}$

信道转移概率为

$p_{Y|X}(y|x)=p_{Z}(y-x)=\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{-\frac{(y-x)^{2}}{2\sigma^{2}}}$ 。

5. 无线衰落信道

无限衰落信道（wireless fading channel）分为时变平衰落信道以及时不变频率选择性衰落信道。涉及到时变时不变的问题，我们就需要讨论一下时变冲激响应以及时变传递函数。

（1）时变冲激响应以及时变传递函数

线性时变系统的冲激响应有两个时间变量，记为 $h(t,\tau)$ 。表示提前 $\tau$ 时间在系统的输入端施加单位冲激（即冲激的位置在 $t-\tau$ 时刻），于t时刻在系统输出端测量的响应。当冲激响应与绝对时间t无关时，该系统退化为线性时不变系统，其单位冲激响应为 $h(\tau)$ 。

若在0时刻施加激励 $x(t)=\delta (t)$ ,t时刻观察到的输出 $y(t)=h (t)$ 。

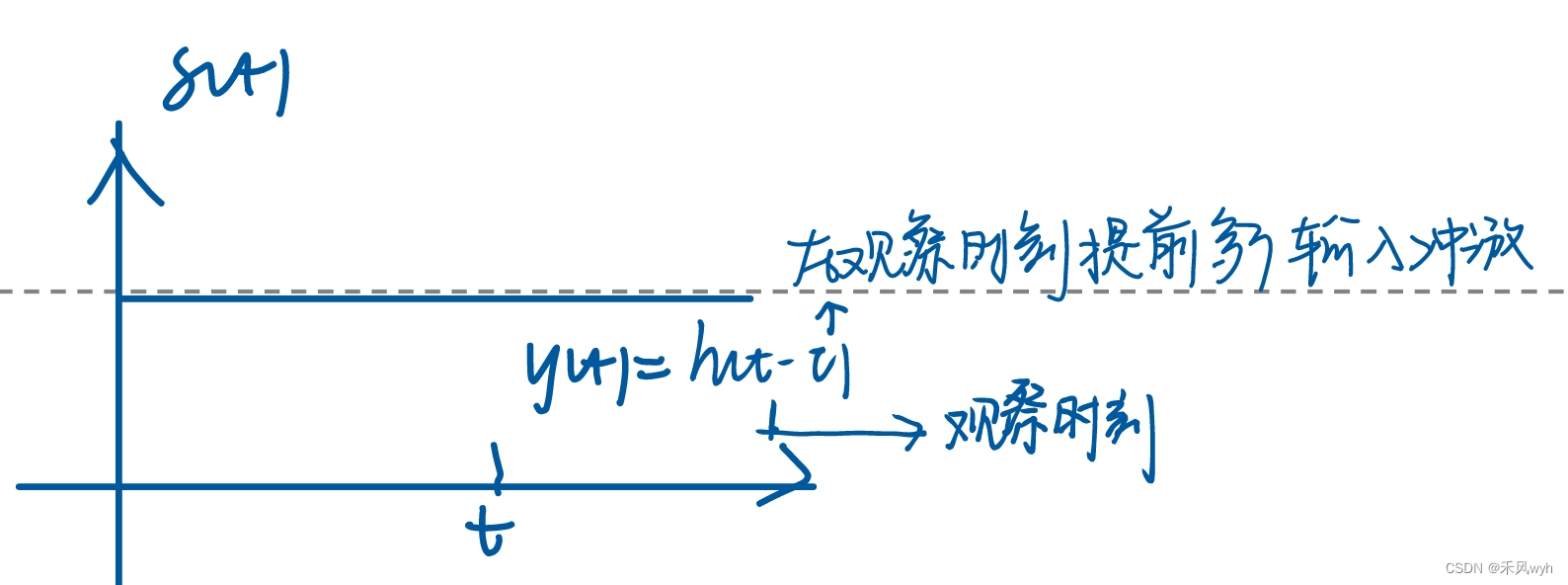
时变信道的时变传递函数时时变冲激响应的傅氏变换

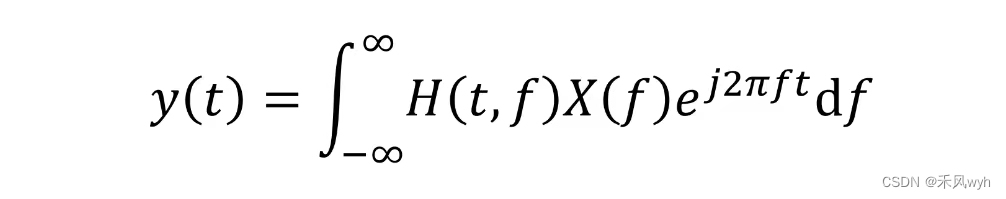
（2）影响通信的因素

无线电波的传播时，传播环境中的各种物体都会影响到电波，例如树木、车辆等。影响电波传播的因素还可能包括天气、海拔、湍流、电离层等。此外，无线通信的收端和发端可能处在运动状态中，运动会造成多普勒频域等问题。这一切都会造成收端收到的电波发生复杂的衰落现象，使信道呈现出随参信道的特征。

总体而言，无限衰落信道影响通信的因素主要有以下两点：

路径损耗（path-loss）：主要是距离原因造成的信号衰减。除距离外，降雨、遮挡、环境造成的电波反射、折射、绕射等也会带来路径损耗。

$P_{r}=P_{t}d^{-\alpha }$ ,α在城市中为3.5-4

快衰落（fast-fading）：主要是环境中的散射体或其他物体的散射、反射、绕射等多径现象带来的信号干扰或色散造成的信号电平快速随机起伏或失真。

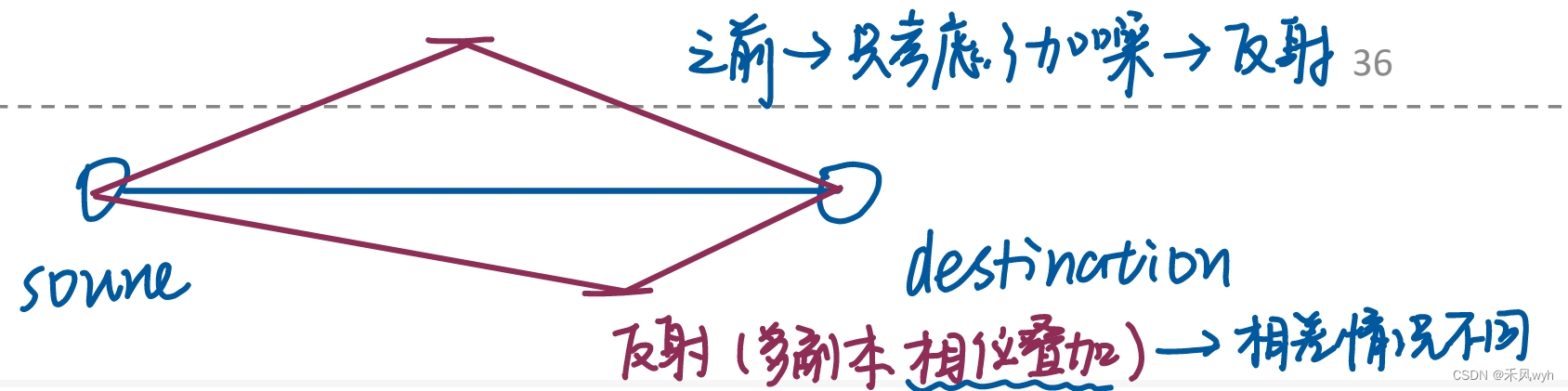
（3）小尺度衰落

主要考虑快衰落带来的影响的时候，我们称衰落为小尺度衰落。信号通过无限衰落信道传输的整个过程可建模为信号先经过一个时变线性系统，然后叠加噪声。由于噪声的存在，衰落也指这种随机性，所以 $h(t,\tau)$ 和 $H(t,f)$ 是随机变量。

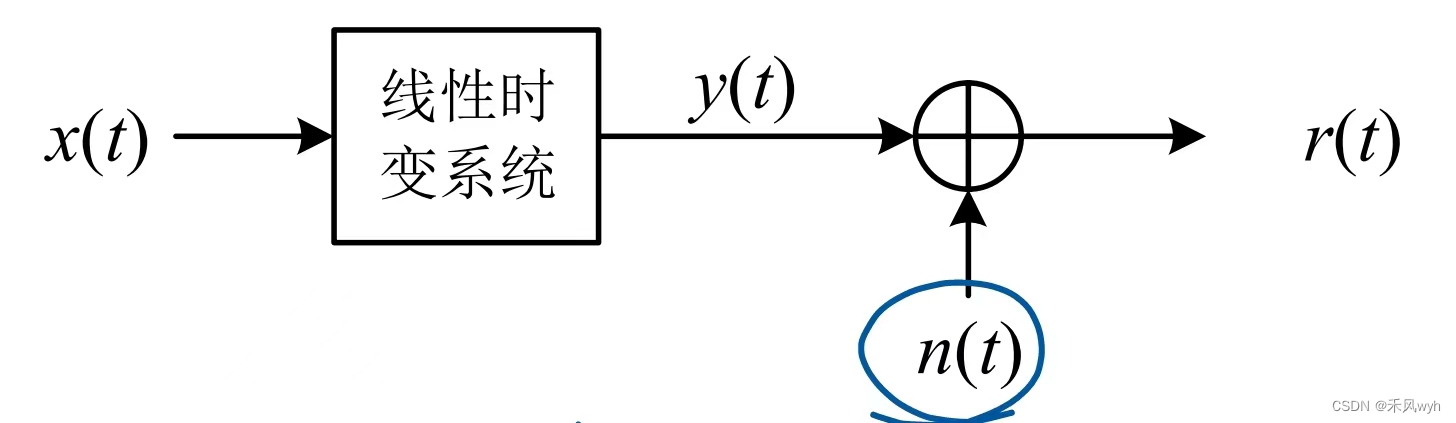
若无线信道的冲激响应是 $h(t,\tau)$ ，则信道输出是 $y(t)=\int_{-\infty}^{\infty}h(t,\tau)x(t-\tau)d\tau$ 。无线信道一般是带通信道，对无线信道的相关分析、建模、仿真都采用等效基带的方法。故对于无限衰落信道，其冲激响应、传递函数都指等效基带冲激响应、等效基带传递函数。

（4）时变平衰落

时变平衰落信道指的是 $H(t,f)$ 与f无关，与t有关，即 $H(t,f)=H(t)$ 。其中，平指传递函数不随频率变化，时变指传递函数随时间变化。

做傅里叶变换，得到冲激响应为：

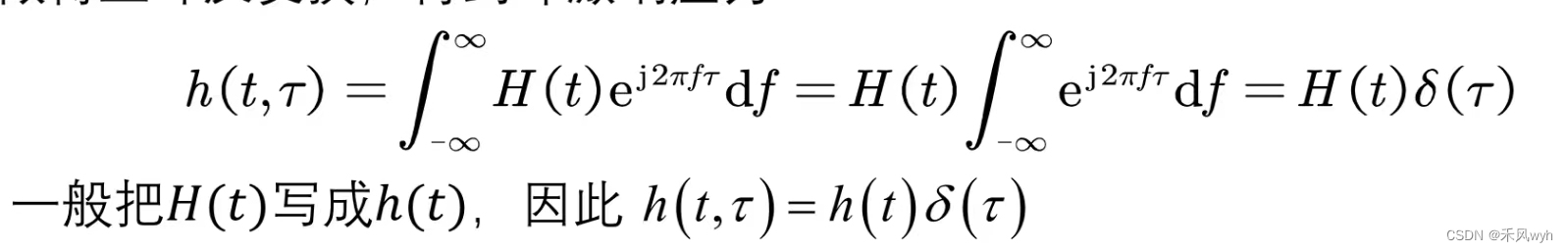
信道输出为

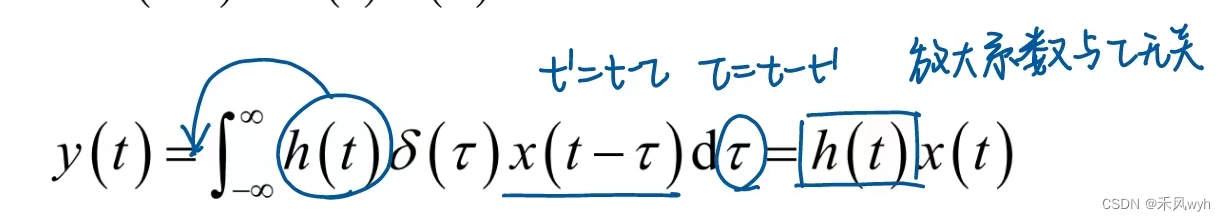
包含噪声时的信道模型为

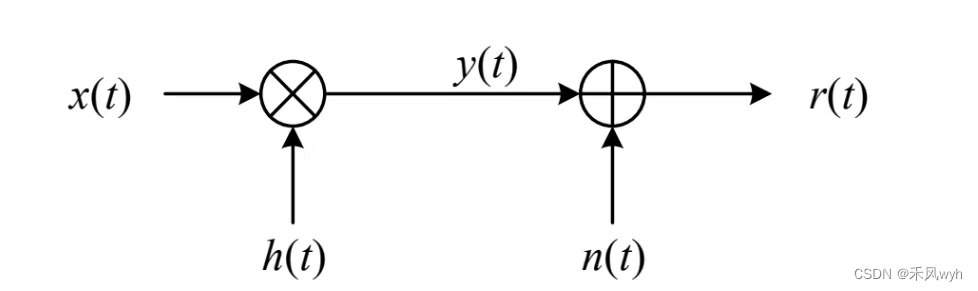
在典型无线通信场景中， $h(t)$ 是平稳复高斯过程，其中复指的是存在实部虚部（I/Q），高斯过程是由多径随机叠加造成的。若 $h(t)$ 的均值为0，则 $|h(t)|$ 服从瑞利分布，称该信道为瑞利信道；若 $h(t)$ 的均值不为0，则 $|h(t)|$ 服从莱斯分布，称该信道为莱斯信道。

平稳随机过程 $h(t)$ 的自相关函数 $R_{h}(\tau)=E[h(t+\tau)h^{*}(t)]$ 与功率谱密度 $P_{h}(f)$ 互为傅氏变换关系。 $R_{h}(\tau)$ 的时域宽度（时宽）称为相干时间， $P_{h}(f)$ 的频域宽度（带宽）称为频域扩展。根据时域频域关系可知，相干时间与频域扩展称反比。相干时间的具体定义有多种，常用定义之一是

$T_{c}=\frac{1}{f_{D}}$

在典型无线通信场景中， $h(t)$ 随t变化的原因是电台在运动，运动会产生多普勒频移。来自不同方向的不同电波有不同的多普勒频移，在频域呈现频谱扩展。因此，信道的频域扩展常常成为多普勒扩展，其值等于最大多普勒频移 $f_{D}$ 。

相干时间 $T_{c}$ 、多普勒频移 $f_{D}$ 反映的是信道 $h(t)$ 随t变化的快慢。电台运动速度越快，则 $h(t)$ 随t变化越快，多普勒扩展 $f_{D}$ 越大，相干时间越小；反之，若电台运动速度越慢，则 $h(t)$ 随t变化越慢，多普勒扩展 $f_{D}$ 越小，相干时间越大。

如果信道不随时间变化，则 $h(t)$ 与t无关，此时 $R_{h}(\tau)$ 是与 $\tau$ 无关的常数，其宽度是无穷大，即时不变信道的相干时间是无穷大。与此同时， $P_{h}(f)$ 做为常数的傅氏变换，是一个冲激，其宽度为0，故时不变信道的频域扩展为0。

以上我们讨论的时变平衰落的时间连续模型，下面，我们将其离散化，得到时间离散模型：

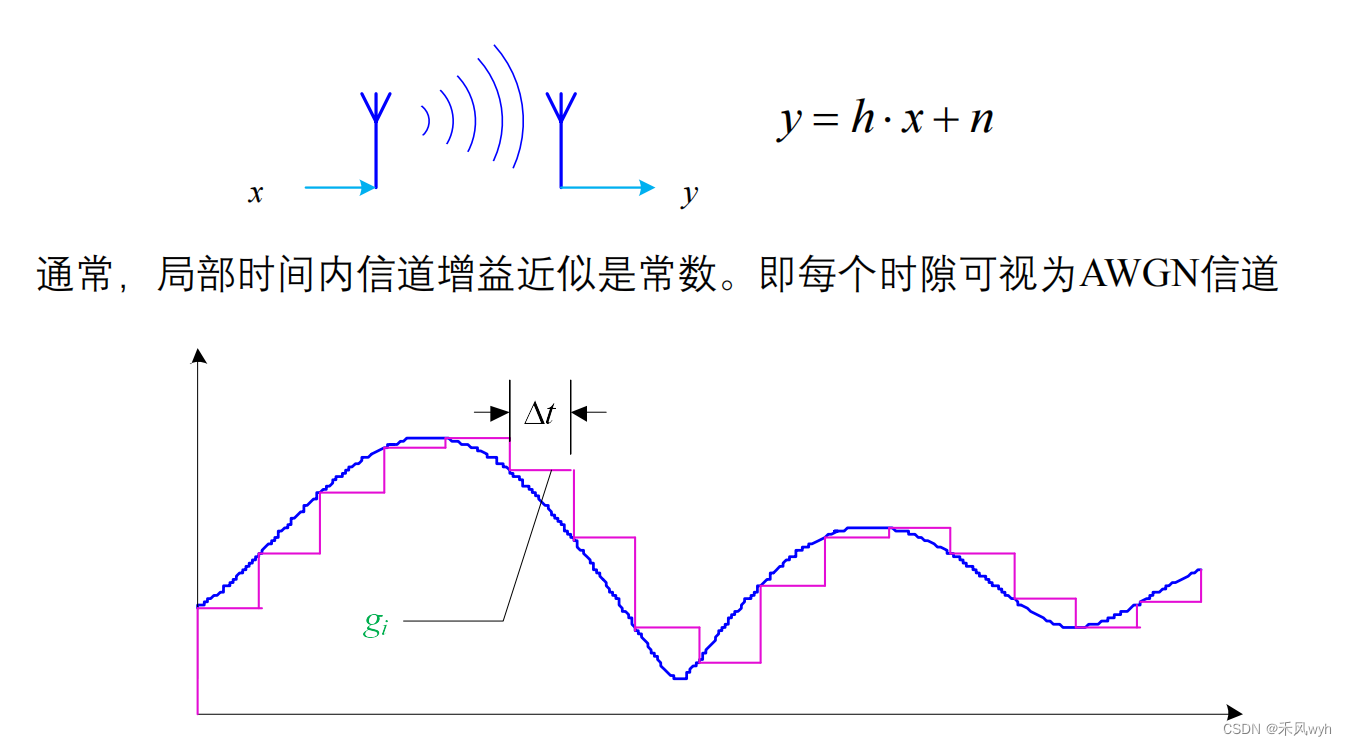
（5）时不变频率选择性衰落信道

时不变频率选择性衰落信道指的是 $H(t,f)$ 随f变，但不随时间t变，即 $H(t,f)=H(f)$ ，其冲激响应为 $h(t,f)=h(\tau)$ ，均与t无关。其中，频率选择性指传递函数随频率变化，时不变指传递函数不随时间变化。

信道输出为

$y(t)=\int_{-\infty}^{\infty}h(\tau)x(t-\tau)d\tau$

$Y(f)=X(f)H(f)$

在典型无线通信场景中， $H(f)$ 是以f为参量的随机过程，其自相关函数为 $E[H(f+\Delta f)H^{*}(f)]$ ，时域对应 $E[|h(\tau)|^{2}]$ 。

时域的 $E[|h(\tau)|^{2}]$ 的宽度称为时延扩展，频域相关函数 $E[H(f+\Delta f)H^{*}(f)]$ 的宽度称为相干带宽。根据时频域关系可知，相干带宽与时延扩展成反比。时延扩展的具体量化定义有多种，例如最大时延扩展、均方时延扩展等。相干带宽 $B_{c}$ 通常定义为时延扩展 $\sigma _{\tau}$ 的倒数：

$B_{c}=\frac{1}{\sigma _{\tau}}$

频率选择性的物理原因通常是多径传播（到达时间不同）。信号经过平衰落信道后，时域不会变宽，所以平衰落信道的时延扩展为0，与此同时，平衰落信道的相干带宽为无穷大。

四、分集（diversity）

衰落信道的信噪比忽高忽低，导致平均BER严重恶化。分集是一种对抗衰落的技术，本质上是用不同的支路传相同的信息，传输多个信号副本。

下图表示发送端用一根天线发送符号x，假设其功率为1，即 $E[|x|^{2}]=1$ ，接收端用一根天线接收端得到y，z是零均值复高斯噪声，其方差为 $\sigma^{2}$ 。接收信号 $y=hx+z$ 的信噪比为 $SNR=\frac{|h|^{2}}{\sigma^{2}}$ ，由于无线信道衰落的随机性， $|h|^{2}$ 是随机变量，因此接受信噪比是随机值，当h因衰落而变小时，信噪比变低，影响接受质量。

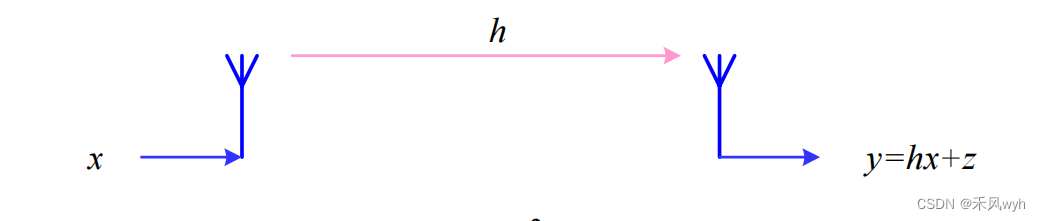
为了解决衰落带来的影响，我们解决方案如下：

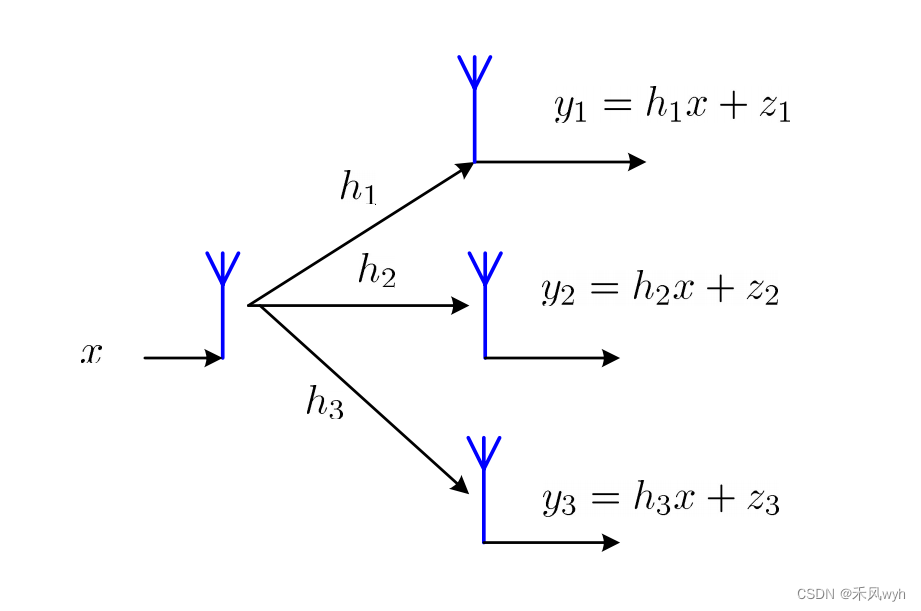
在无限衰落环境下， $h_{1},h_{2},h_{3}$ 都是随机值。如果天线间距足够大， $h_{1},h_{2},h_{3}$ 近似统计独立。此时，某一根天线信噪比变差时，其他天线的信噪比未必变差。至少，三个天线都很差的概率会很小。这种利用多个独立天线来接受，以保障通信可靠性的方法称为分集接受技术。分级技术还有很多，例如，空间分集、时间分集、频率分集、多径分集等。