本文主要是介绍详详详解动归数组常见习题(C/C++),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 最长递增数组序列(必须连续)dp[i] = dp[i - 1] + 1;
- 最长递归子序列(不需要连续)dp[i] = max(dp[i], dp[j] + 1);俩层循环
- 总结一维dp
- 最长重复子数组
- 最长公共子序列
- 总结二维dp
- 最终目标[3692. 最长连续公共子序列 - AcWing题库](https://www.acwing.com/problem/content/3695/)
最长递增数组序列(必须连续)dp[i] = dp[i - 1] + 1;
这个的动态规划比下一个简单一些,但其实大差不差,这个的j不需要遍历i以前的元素,因为我们不求子序列,但是下面的就得求i以前区间的,本题如果不满足 nums[i] > nums[j] 的话 ,那么直接 j=i;更新j指针位置,重新开始计算就好了
卡尔哥完整代码:
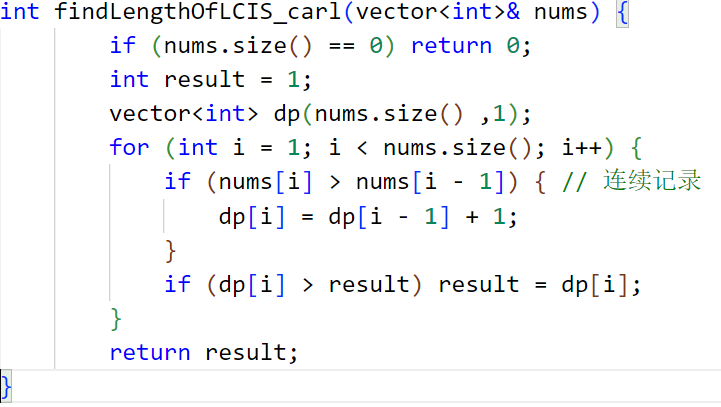
其实根本不需要定义 j 变量,直接 i 与 i-1比较就好了~~
最长递归子序列(不需要连续)dp[i] = max(dp[i], dp[j] + 1);俩层循环
用动态规划
10,9,2,5,3,7,101,18
这组数据放在上个题目的答案就是:3 7 101 三个结果
放在这个题目就是:2 5 7 101 四个结果 这就是子序列的区别
dp[i] 表示:最长子序列的长度(以nums[i]结尾的最长递增子序列的长度)
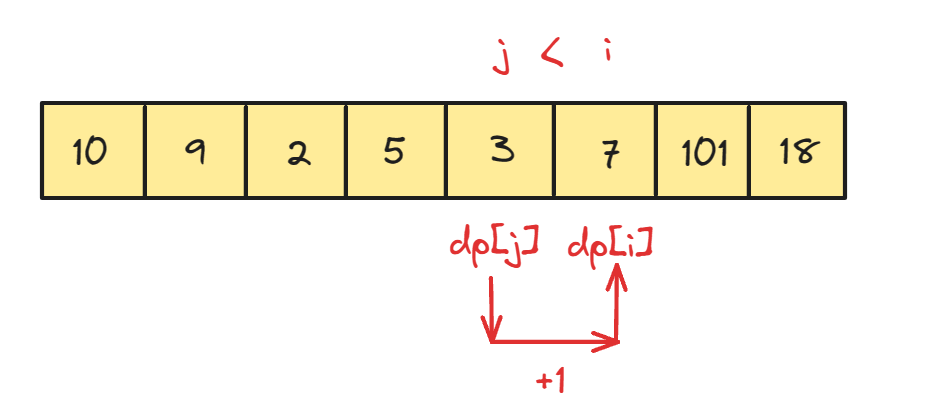
我们的 j 是从 i 以前的区间开始寻找,并不是说i前一个+1就是得到的最终值
每一次j在i之前寻找元素的时候,都会出现一个新的 dp[i] ,所以我们最终的 dp[i] 也要从众多 dp[i] 中找出最大的
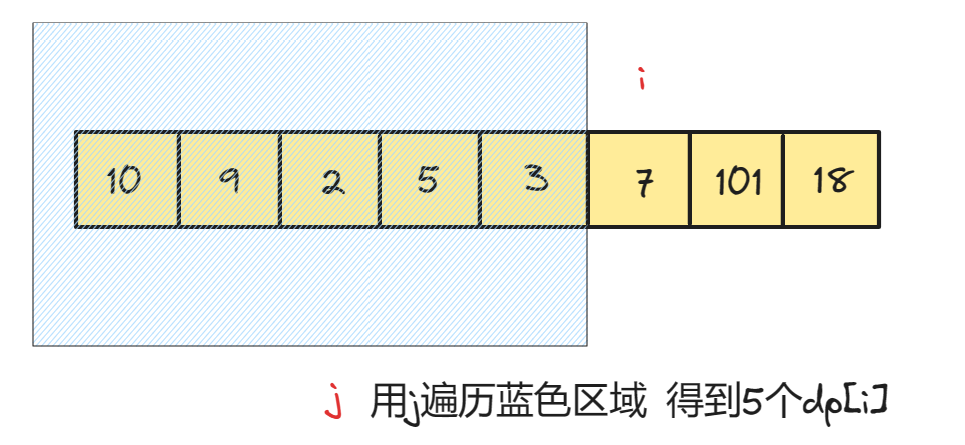
int lengthOfLIS(int* nums, int numsSize) {int dp[numsSize];for (int i = 0; i < numsSize; i++) {dp[i] = 1; // 初始状态,每个数字自身构成长度为 1 的子序列for (int j = 0; j < i; j++) {if (nums[j] < nums[i]) {dp[i] = fmax(dp[i], dp[j] + 1); // 更新 dp[i]}}}int ans = 0;for (int i = 0; i < numsSize; i++) {ans = fmax(ans, dp[i]); // 寻找 dp 数组中最大的值}return ans;
}
总结一维dp
子序列:i 前面的每一个区间的元素 j都要去遍历
必须连续:dp[i] 只与 i 前一个位置 j 进行判断加法
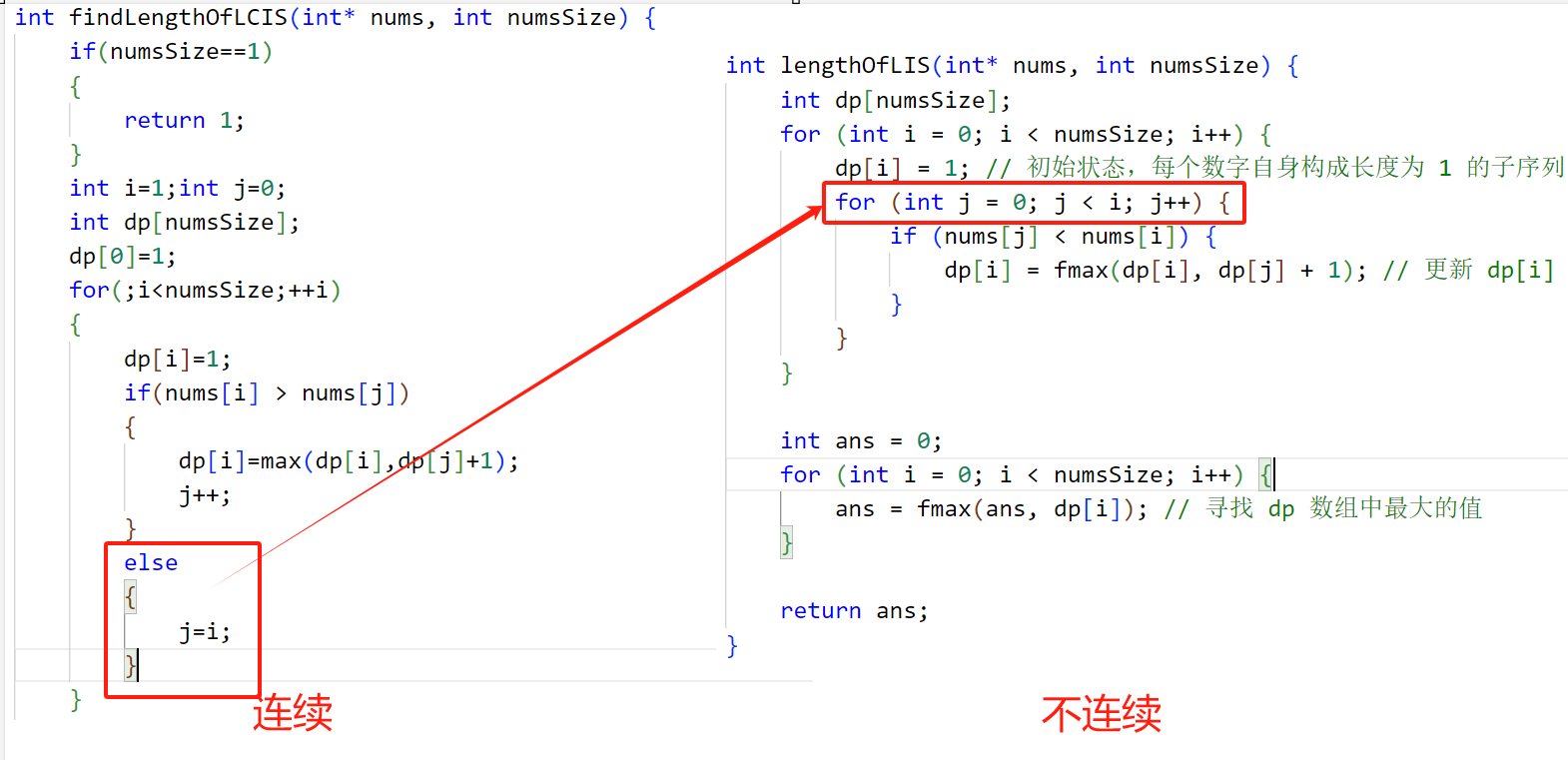
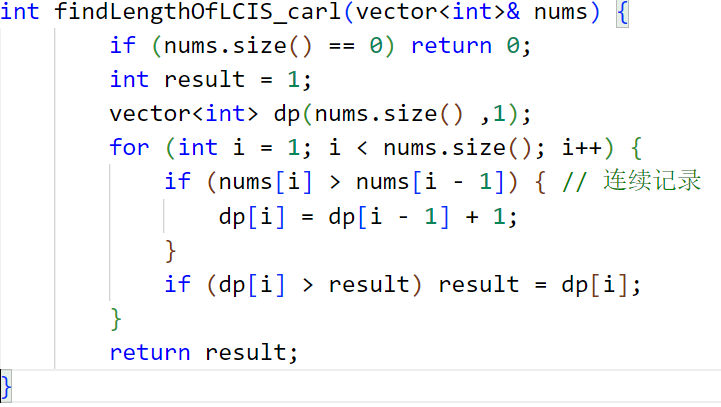
我的代码写的还是太笨了,完全没必要定义 j 变量嘟!!!
最长重复子数组
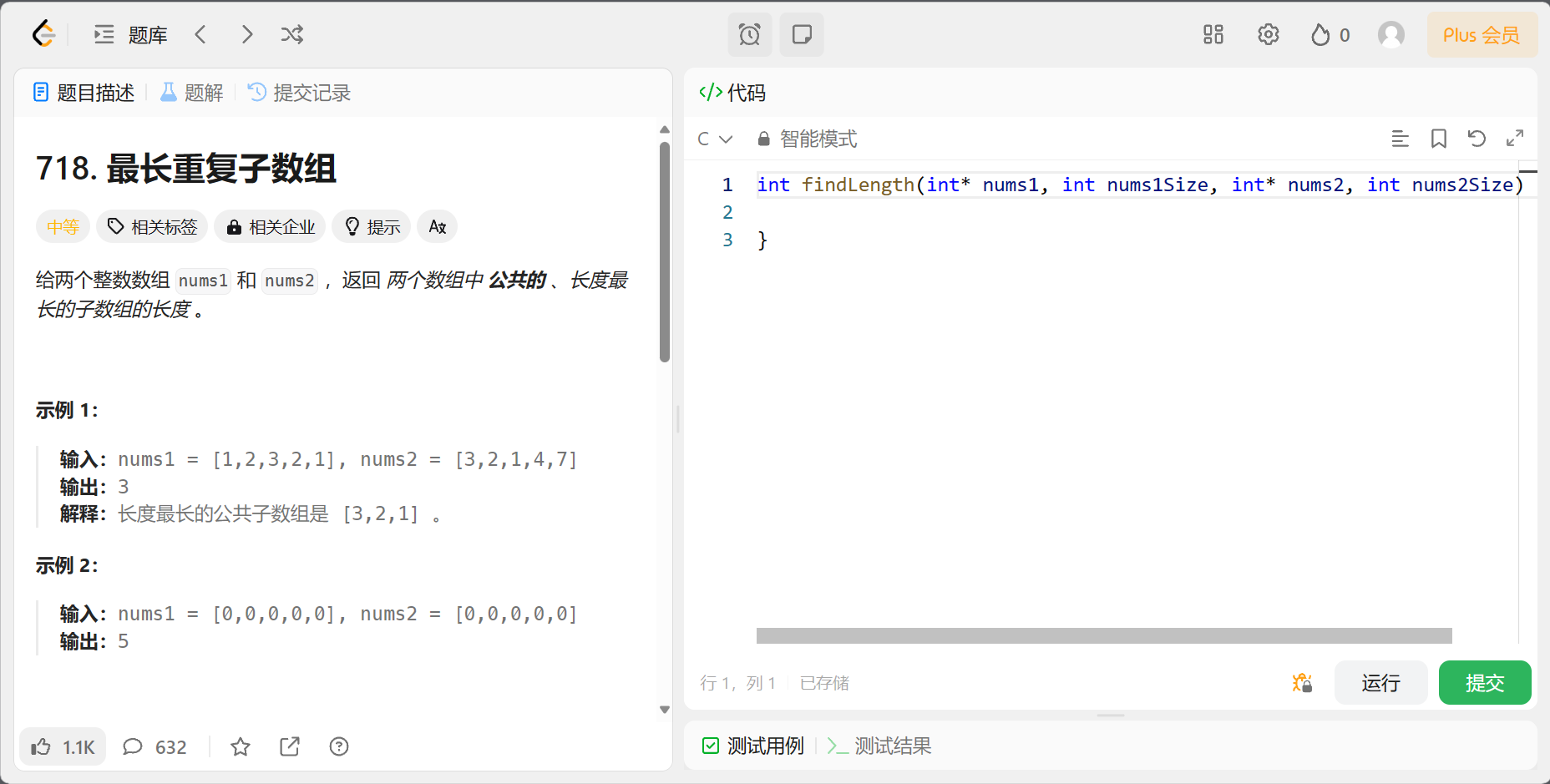
动态规划之子序列问题,想清楚DP数组的定义 | LeetCode:718.最长重复子数组_哔哩哔哩_bilibili
暴力的话,至少是O(N^3) 复杂度非常高
dp数组的含义: dp [i] [j] i 表示 到了nums1数组的元素下标 j 表示到了nums2数组的元素下标
表示 以i-1为结尾的 nums1 和 j-1为结尾的nums2的最长重复子数组长度 也就是说 我们的 dp[i] [j] 的下标比数组慢一步
(以i结尾,以j结尾这样定义后续会很不方便)
递推公式:if(nums1[i-1]==nums2[j-1])dp [i] [j] =dp[i-1] [j-1] +1; 因为我们是以 i-1 j-1 为结尾的dp数组
初始化:根据我们的定义表示,dp[i] [0] dp[0] [j] 都是没有意义的,所以必须初始化为0;对于其他数字我们也可以初始化为0,因为后续也会覆盖,所以直接全部初始化成0就好了
本题也可以进行状态压缩,为了防止覆盖也是从后往前(担心一个值放俩次),类似于01背包
拓展:为什么 i-1 j-1 为结尾 这样初始化很方便,而且越界问题也随着初始化被解决掉了
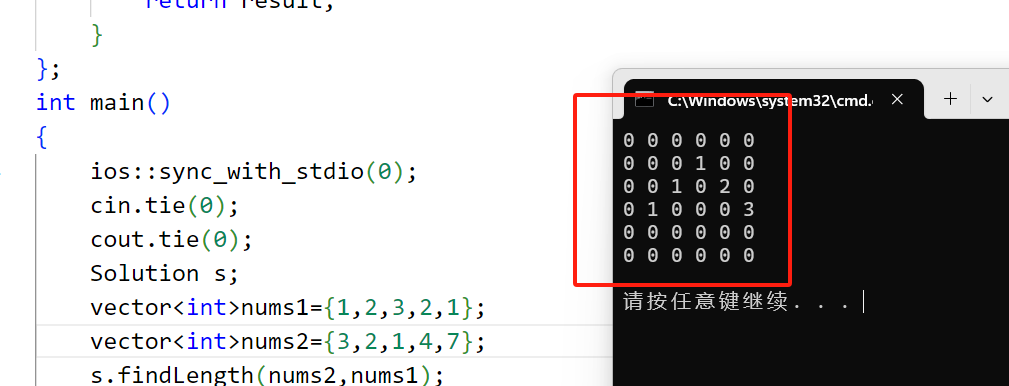
A: 1 2 3 2 1
B 0 0 0 0 0 0
3 0 0 0 1 0 0
2 0 0 1 0 2 0
1 0 1 0 0 0 3
4 0 0 0 0 0 0
7 0 0 0 0 0 0
如果dp数组定义为 i结尾 j结尾的 ,那么就是下面这样:我们必须对刚开始第一行也得初始化判断,而且还要担心越界问题
0 1 2 3 2 1
3 0 0 1 0 0
2 0 1 0 2 0
1 1 0 0 0 3
4 0 0 0 0 0
7 0 0 0 0 0
#include<bits/stdc++.h>
using namespace std;
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int result=0;//代码循环细节,正常来说我们的size就是元素个数,不是数组边界的大小,那么我们i初始化成1 循环终止条件为 i<=size 这样是会发生越界的 但是由于我们的dp数组定义的是 i-1 j-1 为下标的数组,所以我们必须要到达边界,这样才可以访问到我们的最后一个元素 无论是最长递增 还是最长公共 都是 i<nums1Size 这样子的 说明细节真的很多for(int i=1;i<=nums1.size();i++){for(int j=1;j<=nums2.size();j++){if(nums1[i-1]==nums2[j-1])//这个if条件就忘了写了 光顾着写递推公式 连最基本的条件判断都没写{dp[i][j]=dp[i-1][j-1]+1;}if(dp[i][j] > result) result =dp[i][j];//不需要再遍历一次二维数组,我们通过result顺便保存}}for(size_t i=0;i<=nums1.size();i++){for(size_t j=0;j<=nums2.size();j++){cout << dp[i][j] << " ";}cout << endl;}return result;}
};
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);Solution s;vector<int>nums1={1,2,3,2,1};vector<int>nums2={3,2,1,4,7};s.findLength(nums2,nums1);return 0;
}
代码中有一个很大的bug:int dp [nums1Size+1] [nums2Size+1]={{0}}; //报错原因 不支持动态开辟二维数组
所以我们还是用vector来进行初始化和运算更方便一些
vector<vector> dp (nums1.size() + 1, vector(nums2.size() + 1, 0));
代码解释:这里运用了构造,nums.size()+1个vector,每一个vector又是nums2.size()+1个0
最长公共子序列
0 a b c d e
0 0 0 0 0 0 dp[0] [j]
a 0 1 1 1 1 1
c 0 1 1 2 2 2
e 0 1 1 2 2 3
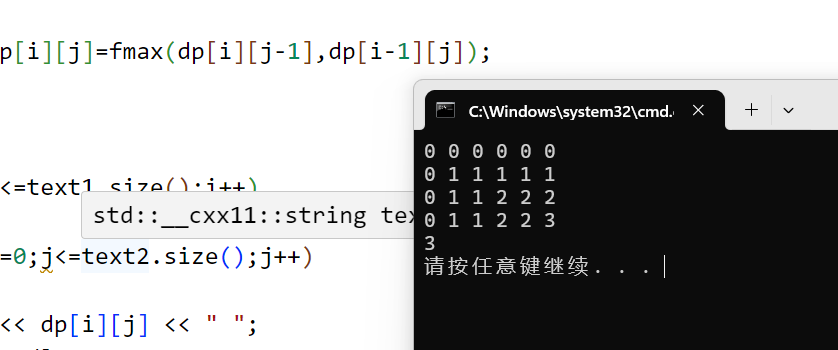
dp[i] [j]:表示以 i-1 j-1 的最长公共子序列 一般来说 dp中用来二维的都是定义到 i-1 j-1 其实也很好理解 就像蓝桥杯的扫雷那个题目,我们如果对数组不进行扩充处理的话,就要对第一行和第一列进行特殊情况的判断,这个道理在本题中也是同样的道理
递推公式: if(nums1[i-1]==nums2[j-1])dp [i] [j] =dp[i-1] [j-1] +1;
为什么我们if条件中写的是 i-1 j-1 呢?因为我们是以 i-1 j-1 为结尾的dp数组
if(nums1[i-1] != nums2[j-1])
对于 a b c 与 a c e 此时c 与 e不相同 那么 我们可能考虑 a b c与 a c匹配 :dp[i] [j-1]
对于 a b c 与 a c e 我们也可能考虑 a c e与 a b匹配 :dp[i-1] [j]
这俩种情况都有可能是我们的dp[i] [j]
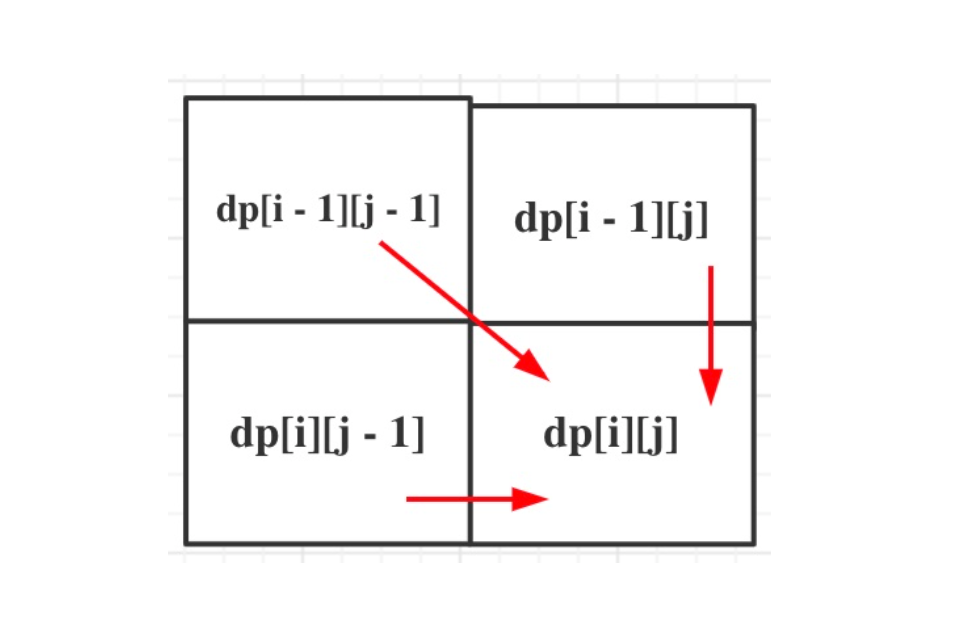
初始化:我们的第一行第一列全部初始化为0 含义是 空字符与字符匹配结果为0
而且我们遍历的时候是 从左往右 从上往下遍历
而且这个题目不需要去遍历寻找最大值 dp[text1.size()] [text2.size()] 就是我们最终求得的结果 与上题的result不一样
总结二维dp
1.初始化
vector<vector<int> > dp (text1.size()+1,vector<int>(text2.size()+1,0));
刚开始多初始化一行一列,对于解决二维dp有大帮助,省去越界与单独情况特判的麻烦
2.递推公式
if(nums1[i-1]==nums2[j-1])dp [i] [j] =dp[i-1] [j-1] +1;
这其实就是斜对角线
3.代码对比

不同点:
返回值的返回方式不同
递推公式不同,子序列要考虑更多的情况
相同点:
初始化的方式相同
循环控制的终止条件相同
最终目标3692. 最长连续公共子序列 - AcWing题库
最长连续公共子序列 = 最长重复子数组的题目 递推公式只有一个,求的不是子序列而是连续的
将上述代码改吧改吧
#include<bits/stdc++.h>
using namespace std;
class Solution {
public:int findLength(string& nums1, string& nums2) {vector<vector<int>> dp (nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int result=0;for(int i=1;i<=nums1.size();i++){for(int j=1;j<=nums2.size();j++){if(nums1[i-1]==nums2[j-1])//这个if条件就忘了写了 光顾着写递推公式 连最基本的条件判断都没写{dp[i][j]=dp[i-1][j-1]+1;}if(dp[i][j] > result) result =dp[i][j];//不需要再遍历一次二维数组,我们通过result顺便保存}}return result;}
};
int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);Solution s;string s1;string s2;cin >> s1;cin >> s2;cout << s.findLength(s1,s2);return 0;
}
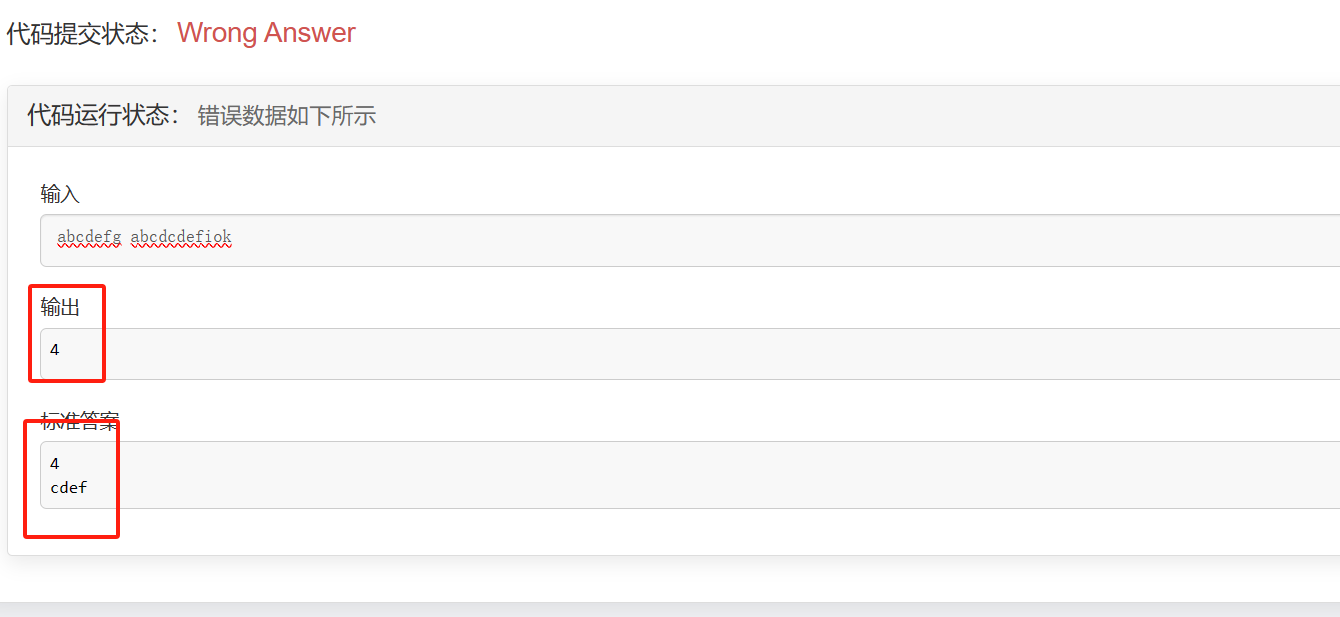
关于有序字符的输出,现在的我还是无法解决…
这篇关于详详详解动归数组常见习题(C/C++)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





