本文主要是介绍递归专题---如何优雅的编写递归函数,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、递归函数的编写
二、题目练习
1、汉诺塔----点击跳转题目
2、合并两个有序链表---点击跳转题目
3、反转链表----点击跳转题目
在计算机科学中,递归是一种重要的概念和技术。它允许函数直接或间接地调用自身,以解决复杂的问题。
递归的基本思想是将一个大问题分解成若干个较小的、相似的子问题,然后通过不断地递归调用自身来解决这些子问题,直至达到基本情况。
递归在许多领域都有广泛的应用,如算法设计、数据结构处理等。它可以帮助我们更简洁、优雅地解决一些原本复杂的问题。
在算法题中,我们什么时候会使用递归,为什么会使用递归呢?当我们分析一道算法题时,发现主问题可以划分为相同的子问题,此时就可以考虑使用递归。
对于递归,我们可以尝试理解其中的运作原理,但在编写一道算法题时,其实大可不必,并且总是思考递归的细节还会影响我们编写的速度,递归其实就是用函数的栈帧帮助我们保存信息以及自动回退到上一层问题,针对一道题,如何编写递归呢?
一、递归函数的编写
对于一个递归函数,我们可以把它分为三部分:函数头、函数主体、递归出口;分别思考每一部分如何设计即可!
- 先找到相同的子问题--->函数头; 对于找到的相同的子问题,我们就该考虑怎么解决这些相同的问题,思考函数的功能该如何定义?需要传入哪些参数?此时,一个递归函数的函数头已经完成。
- 只关心某一个子问题如何解决---->函数体;完成函数头的定义后,我们把目光从观察多个子问题转变到聚焦于某一个子问题,思考如何通过定义的函数功能来解决这一个子问题(此时就会出现递归调用)。
- 找到不可再划分的子问题---->递归出口;递归函数在层层调用解决相同子问题时这些子问题的相同只是解决方式相同,但是问题的规模是在逐渐变小的,当达到某个条件时子问题不可再划分,此时就是递归出口(通过条件判断结束函数调用)。
二、题目练习
1、汉诺塔----点击跳转题目

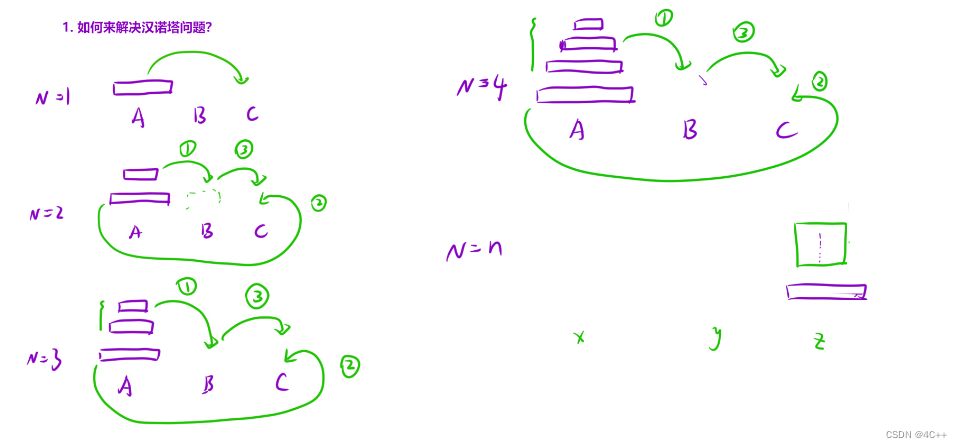
通过推演可以发现,无论A有多少个盘子,解决的思路都是,先把A上的n-1个盘子移动到B,在把A中最后一个盘子(也是最大的盘子)移动到C,再把B上的n-1个盘子移动到C上,如何移动呢?先把B上的n-2个盘子移动到A,再把B上的最后一个盘子.........
我们可以发现,每个子问题,除了移动盘子的起始柱子和目标柱子不一样,但是每次对盘子的操作方式都是一样的,通过辅助柱子来放置上面的盘子,再把起始柱子上最大的盘子移动到目标柱子,再递归的把刚才辅助柱子上的盘子移动到目标柱子(此时上一步的辅助柱子在这一步中就作为了起始柱子)




如何编写解决汉诺塔问题的递归函数呢?
- 函数头:每个子问题都是把起始柱子的n个盘子通过辅助柱子合法的移动到目标柱子;递归函数的功能就可以如上定义,需要的参数就是三个柱子分别扮演的角色和需要移动的盘子个数 ----> 将x柱子上最上面的n个盘子借助y柱子转移到z柱子上。
dfs(vector<int>& x,vector<int>& y,vector<int>& z,int n)
- 函数体:
先把起始柱子的n-1个盘子移动到移动到辅助柱子:
dfs(x,z,y,n-1);再把起始柱子上剩下的一个盘子移动到目标柱子上:
//模拟移动盘子的过程 z.push_back(x.back());x.pop_back();最后把辅助柱子上的盘子递归的移动到目标柱子上:
dfs(y,x,z,n-1);//这个函数调用后,辅助柱子就作为了起始柱子
- 递归出口:当起始柱子上只有一个盘子时,只需要把盘子移动到目标柱子,此时问题不可再分。
if(n == 1) {z.push_back(x.back());x.pop_back();return ;}
完整代码;
class Solution {
public://将x柱子上最上面的n个盘子借助y柱子转移到z柱子上void dfs(vector<int>& x,vector<int>& y,vector<int>& z,int n){if(n == 1) {z.push_back(x.back());x.pop_back();return ;}dfs(x,z,y,n-1);z.push_back(x.back());x.pop_back();dfs(y,x,z,n-1);}void hanota(vector<int>& A, vector<int>& B, vector<int>& C) {dfs(A,B,C,A.size());}
};2、合并两个有序链表---点击跳转题目
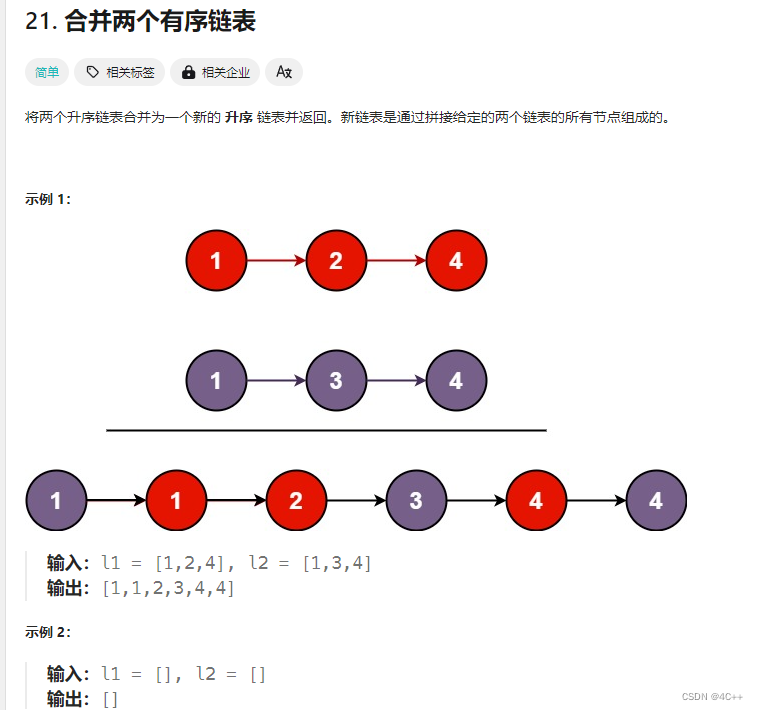
本题可以循环解决,主要研究如何递归解决,循环方法不过多叙述
递归理解:对于两个链表每一个结点,我们都是返回最小的结点,并让这个结点后面的链表与另一个链表合并
算法思路:
- 递归函数的含义:交给你两个链表的头结点,你帮我把它们合并起来,并且返回合并后的头结点;
- 函数体:选择两个头结点中较⼩的结点作为最终合并后的头结点,然后将剩下的链表交给递归函数 去处理,再把返回的头节点连接起来。
- 递归出⼝:当某⼀个链表为空的时候,返回另外⼀个链表。
代码:
class Solution {
public:ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {if(!list1) return list2;if(!list2) return list1;ListNode* ret;if(list1->val < list2->val){ret = list1;list1 = list1->next;ret->next = mergeTwoLists(list1,list2);}else{ret = list2;list2 = list2->next;ret->next = mergeTwoLists(list1,list2);}return ret;}
};3、反转链表----点击跳转题目
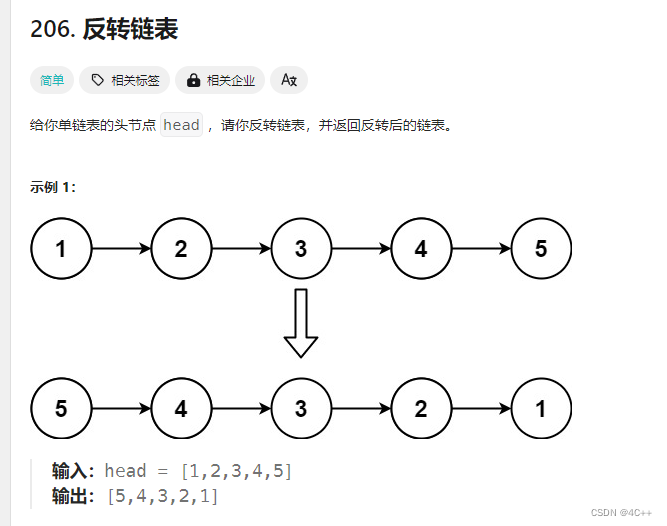
本题也可以用循环解决(创捷一个虚拟头节点,遍历链表不断对虚拟头节点做头插操作)
递归如何解决呢?
给你一个链表,返回反转后的链表头节点,相同子问题就是反转链表
算法思路:
- 递归函数的含义:交给你⼀个链表的头指针,你帮我逆序之后,返回逆序后的头结点;
- 函数体:先把当前结点之后的链表逆序,逆序完之后,把当前结点添加到逆序后的链表后⾯即可;
- 递归出⼝:当前结点为空或者当前只有⼀个结点的时候,不⽤逆序,直接返回。
代码:
class Solution {
public:ListNode* reverseList(ListNode* head) {if(head == nullptr || head->next == nullptr) return head;ListNode* newHead = reverseList(head->next);head->next->next = head;head->next = nullptr;return newHead;}
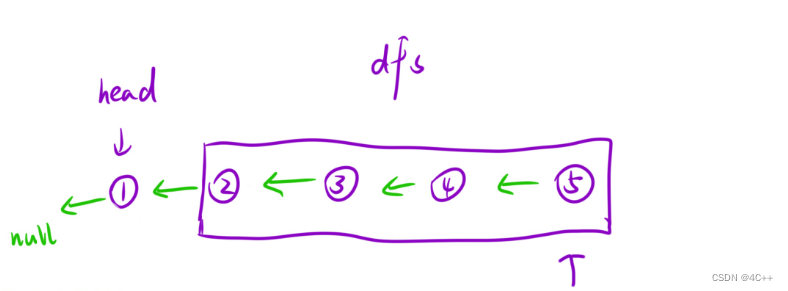
};其实这份代码还有一种解读的视角,把这条链表看作是一根树,对树做DFS,直到遍历到最后一个结点,在每一次在回到上一层时该改变指针的指向,并把两个结点间的较上层的结点的next置为空(这一步是为了统一操作,把原来的其实结点的next置空)
置为空并不影响找到之前的结点,因为DFS时通过递归调用已经把结点信息都存储在函数栈帧中了
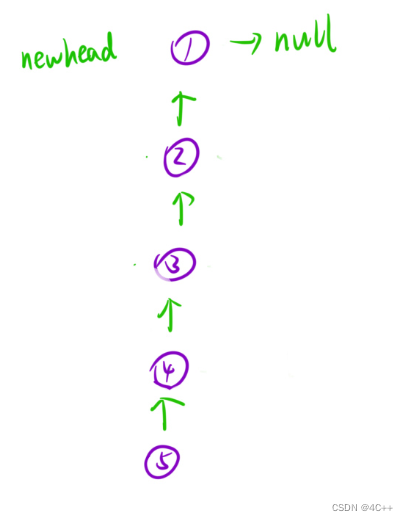
通过上面的题目练习,是不是对递归更加熟悉与了解了呢?其实在编写和理解递归函数时,我们要把递归函数当成一个能一定完成任务的黑盒,坚定不移的相信它可以完成它的使命,我们只需在递归函数中在合适的时机自信的调用它即可!
下一篇博客,会继续通过算法题来练习递归,敬请期待.....
这篇关于递归专题---如何优雅的编写递归函数的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




