本文主要是介绍IPM原理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
IPM原理
- 1. 什么是IPM
- 2. 鸟瞰图拼接
- 3. Ipm鸟瞰图效果
这里只是简单记录IPM的原理思想和应用,工程中还需考虑很多的影响,比如说pitch角等
1. 什么是IPM
IPM变换就是消除这种透视效应,所以也叫逆透视。原本平行的两条车道线,在针孔相机下因为透视变换,在图片中看到的效果并不平行,这是因为透视现象。而IPM的思想可以将原来的透视结果转换到鸟瞰图的视野下,看到的车道线也是水平的。
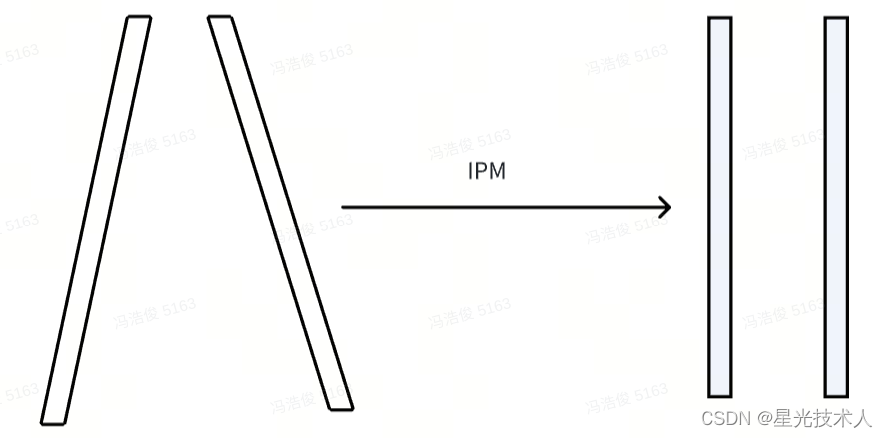
透视变换的作用是让我们从另外一个角度观察图片中的场景,例如俯视。它能帮助我们避免例如“近大远小”造成的图像世界与现实世界的偏差,其方法的本质是“映射”,将原图像的像素点按照一定的“比例”映射到另外一张图上。
IPM变换具有很多应用,求取IPM图像的方法亦是有很多。
IPM的本质是切换视野,比如将原来的视图切换到BEV视野下。
在不知道相机的参数的情况下,拍摄两张不同角度,但是有重复视野的图片。通过得到两张图片中重合视野部分的特征对应点,构建一系列方程,就可以得到两个视野之间的单应矩阵,完成视野之间的切换,但是需要注意的是,图片A变换到图片B的视野,图片包含的信息还是图片A的信息,只是视野重合的部分之间一致。
-
为什么两个不同的视野之间的变换,可以使用一个单应性矩阵代替?
因为可以假定空间中有一个点P, 两个相机坐标系 C A , C B C_A,C_B CA,CB。两个相机的内外参已知,那么通过内外参可以得到点P在两个像素坐标系中的像素坐标。详细步骤请看,
[ u A v A 1 ] = λ A ⋅ I A ⋅ [ r A 1 r A 2 r A 3 t A ] ⋅ [ X w Y w Z w 1 ] [ u B v B 1 ] = λ B ⋅ I B ⋅ [ r B 1 r B 2 r B 3 t B ] ⋅ [ X w Y w Z w 1 ] [ X w Y w Z w 1 ] = 1 λ A [ r A 1 r A 2 r A 3 t A ] − 1 ⋅ I A − 1 [ u A v A 1 ] [ X w Y w Z w 1 ] = 1 λ B [ r B 1 r B 2 r B 3 t B ] − 1 ⋅ I B − 1 [ u B v B 1 ] [ u A v A 1 ] = λ A λ B ⋅ I A ⋅ [ r A 1 r A 2 r A 3 t A ] ⋅ [ r B 1 r B 2 r B 3 t B ] − 1 ⋅ I B − 1 [ u B v B 1 ] \begin{align} \begin{bmatrix} u_A \\ v_A \\ 1 \end{bmatrix} &= \lambda_A \cdot I_A \cdot \begin{bmatrix} r_{A1} & r_{A2} & r_{A3} & t_A \end{bmatrix} \cdot \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix} \\ \begin{bmatrix} u_B \\ v_B \\ 1 \end{bmatrix} &= \lambda_B \cdot I_B \cdot \begin{bmatrix} r_{B1} & r_{B2} & r_{B3} & t_B \end{bmatrix} \cdot \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix} \\ \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix} &= {1 \over \lambda_A} \begin{bmatrix} r_{A1} & r_{A2} & r_{A3} & t_A \end{bmatrix} ^ {-1} \cdot I_A^{-1} \begin{bmatrix} u_A \\ v_A \\ 1 \end{bmatrix} \\ \begin{bmatrix} X_w \\ Y_w \\ Z_w \\ 1 \end{bmatrix} &= {1 \over \lambda_B} \begin{bmatrix} r_{B1} & r_{B2} & r_{B3} & t_B \end{bmatrix} ^ {-1} \cdot I_B^{-1} \begin{bmatrix} u_B \\ v_B \\ 1 \end{bmatrix} \\ \begin{bmatrix} u_A \\ v_A \\ 1 \end{bmatrix} &= {\lambda_A \over \lambda_B} \cdot I_A \cdot \begin{bmatrix} r_{A1} & r_{A2} & r_{A3} & t_A \end{bmatrix} \cdot \begin{bmatrix} r_{B1} & r_{B2} & r_{B3} & t_B \end{bmatrix} ^ {-1} \cdot I_B^{-1} \begin{bmatrix} u_B \\ v_B \\ 1 \end{bmatrix} \end{align} uAvA1 uBvB1 XwYwZw1 XwYwZw1 uAvA1 =λA⋅IA⋅[rA1rA2rA3tA]⋅ XwYwZw1 =λB⋅IB⋅[rB1rB2rB3tB]⋅ XwYwZw1 =λA1[rA1rA2rA3tA]−1⋅IA−1 uAvA1 =λB1[rB1rB2rB3tB]−1⋅IB−1 uBvB1 =λBλA⋅IA⋅[rA1rA2rA3tA]⋅[rB1rB2rB3tB]−1⋅IB−1 uBvB1
由式(5)可以得出,同一个点在两个不同位置相机的像素坐标系中的像素坐标之间存在一个变换关系,这里的相机内外参已知,所以可以直接记单应矩阵 H H H为,
H = λ A λ B ⋅ I A ⋅ [ r A 1 r A 2 r A 3 t A ] ⋅ [ r B 1 r B 2 r B 3 t B ] − 1 ⋅ I B − 1 H = {\lambda_A \over \lambda_B} \cdot I_A \cdot \begin{bmatrix} r_{A1} & r_{A2} & r_{A3} & t_A \end{bmatrix} \cdot \begin{bmatrix} r_{B1} & r_{B2} & r_{B3} & t_B \end{bmatrix} ^ {-1} \cdot I_B^{-1} H=λBλA⋅IA⋅[rA1rA2rA3tA]⋅[rB1rB2rB3tB]−1⋅IB−1
这是在已知两个相机的外参和内参的情况下,可以直接获取两者的单应变换。但是如果不知道两个相机的内外参数,只有两张图片,怎么通过两张图片得到两者的单应矩阵?这就需要2D to 2D的非线性优化方式了。 -
直接使用两张不同视野下的图片(图片视野有重合),怎么直接得到单应矩阵?

需要注意的是,为什么单应矩阵只有8个自由度

2. 鸟瞰图拼接
这里介绍一种,将车身周围多个相机视野拼接为一个全BEV视野俯视图的方式,也是BEV感知中,将2D图片的feature给到BEV空间的基本思路。可以理解为一个映射的过程
- 已自车为原点,选定感知范围,比如纵向前后50m,横向左右30m。设置栅格分辨率为0.1m,得到大小为 600 × 1000 600 \times 1000 600×1000的栅格图
- 建立空的cv::Mat画板,大小为 600 × 1000 600 \times 1000 600×1000
- 遍历栅格图,利用相机内参外完成栅格中心点的自车系坐标到像素坐标系的转化,得到对应的原相机像素坐标,并将这个像素的三个颜色通道赋值给BEV栅格
3. Ipm鸟瞰图效果
内部图 不方便展示
Ipm鸟瞰图效果
https://yanyx.blog.csdn.net/article/details/104791610
https://blog.csdn.net/feiyang_luo/article/details/103555036
这篇关于IPM原理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





