noip2019集训测试赛（二）A.余数

本文主要是介绍noip2019集训测试赛（二）A.余数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Description

---

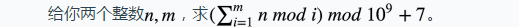
Input

---

Output

---

Solution

整除分块：https://blog.csdn.net/gdhy9064/article/details/90112836

通过整除分块，我们可以得到对于每个x $\lfloor \frac{n}{x}\rfloor$的值，那么可以转化原式：

${\sum }_{i=1}^{n}n\mathrm{m}\mathrm{o}\mathrm{d}i={\sum }_{i=1}^{n}i\ast n-\lfloor \frac{n}{x}\rfloor \ast x$。

利用等差数列公式，可以在$O(\sqrt{n})$的时间复杂度内计算${\sum }_{i=1}^{\min (n,m)}$的值。
若m>n，那么加上$(m-n)\ast n$就好了。

---

Code

#include<bits/stdc++.h>
using namespace std;
const int mod=1e9+7;
long long n,m,ans,l=1,r;
int main(){scanf("%lld%lld",&n,&m);while(l<=n&&l<=m){r=min(n/(n/l),m);long long sum1,sum2;sum1=(r-l+1)%mod*(n%mod)%mod;if((r-l)%2==1) sum2=((r-l+1)/2%mod*((l+r)%mod)%mod*((n/l)%mod)%mod)%mod;else sum2=(((l+r)/2%mod)*((r-l+1)%mod)%mod*((n/l)%mod)%mod)%mod;ans=(ans+(sum1-sum2+mod)%mod)%mod;l=r+1;}if(n<m) ans=(ans+(m-n)%mod*(n%mod)%mod)%mod;printf("%lld",ans);
}

这篇关于noip2019集训测试赛（二）A.余数的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---