本文主要是介绍科普如何做到既专业又易懂?这五种方法值得一试,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
学习数学或者其他理论会很难,但学得深入了,口中就充斥着大量的专业名词,向不是该领域的受众介绍又变成了另外一件难事。近年来我也一直在做数学科普的工作,经常面对的挑战是如何将这些充满术语的复杂理论用简单明了的方式表达给广大读者。其实如何将这些抽象的理论和复杂的数据转化为容易理解的信息,是每一位科技工作者和教育者必须面对的问题。本文将介绍五种主要工具来帮助我们更好地解释和理解技术性概念。
1. 数学公式和定义
数学是科学的语言。通过公式和定义,我们能够精确描述和探索自然法则。例如,要解释“卷积”这一数学概念,我们首先需要知道它涉及的数学表达式。卷积是统计学中的一种方法,通过这种方法可以将两个独立随机变量的概率分布组合起来,以估计这两个变量之和的分布。其数学表达是:
在解释如何模拟疾病传播或人口增长时,指数增长模型提供了一个精确的描述方式。指数增长可以通过下面的公式来定义:
其中, 表示时间 时的总人口或感杂人数, 是初始人口或感染人数, 是增长率, 是自然对数的基底。这个公式不仅清䀿地表达了增长的快速性,也可以预测未来发展。
2. 示例
理论与实践的结合可以极大地增强理解。继续使用卷积的例子,我们可以考虑一个简单的情景:掷两个骰子的总点数的概率分布。单独一个骰子的点数分布是均匀的,但当我们将两个骰子的结果相加时,总和的分布形状会发生变化,变得中间高两端低,这正是卷积的直观表现。
通过具体计算每种点数组合的概率,我们不仅能够展示卷积的具体应用,也让抽象的公式有了直观的图像化表达。
3. 图像
图像是传达科学概念的强有力工具。在卷积的例子中,我们可以使用图表来展示两个独立骰子点数的概率分布以及它们卷积后的总和分布。
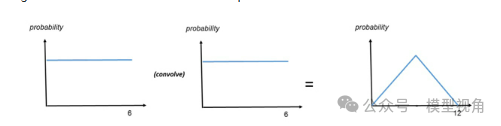
图像可以帮助观众直观地看到分布从均匀过渡到有峰的过程,这种视觉上的直观感受常常比文字和公式更为直接和有效。
在解释声波或电磁波的传播时,正弦波图像是理想的视觉辅助工具。通过展示一个正弦波的图像,可以直观地看到波的波峰、波谷以及波长和振幅,这些都是波动现象的关键特征。图像能够帮助读者直观地理解波的周期性变化以及波动的基本属性。

4. 故事
科学与故事结合,可以让听众在情感上与所讲解的概念建立连接。比如,解释均值的概念时,可以通过比喻说它是概率分布的“重心”。可以想象,如果将这个分布的形状剪出来放在一个平衡点上,它会在均值处保持平衡。这种通过日常生活经验的类比,使得抽象的数学概念变得生动和易懂。

在解释万有引力定律时,经常会用到牛顿观察苹果落地的故事。据说牛顿在看到苹果从树上掉落时灵光一现,从而提出了万有引力的概念。这个故事不仅生动有趣,还能帮助读者理解科学理论常常是从日常生活的观察中诞生的,这种情境化的讲述方式能够增加概念的吸引力和记忆点。
5. 演示
动态演示是理解物理现象中动态过程的有效方式。例如,在解释共振的概念时,我们可以通过实验演示一个摆动的秋千。通过调整推秋千的频率匹配自然频率,可以使秋千摆动的幅度最大。这种实验不仅可以直观展示共振的物理过程,还能加深学习者对频率、周期及其互相影响的理解。
在解释电解质如何导电时,演示盐水导电是一个直观的实验。在这个演示中,将两个电极插入盐水中,并接入电源,可以观察到灯泡点亮。这个实验不仅展示了盐水作为电解质的导电性,还直观地证明了溶解的离子是如何帮助完成电流的传导的。
这五种工具各有所长,合理使用可以大大提高技术性概念的传达效果。在实际应用中,通常需要根据目标听众的背景和具体的教学目标灵活选择适合的方法。例如,对于科学背景较强的听众,更多的使用数学公式和定义可能更为有效;而对于普通公众,则可能需要更多的图像、故事和演示来帮助他们建立直观理解。——王海华
在科学传播和教育的实践中,我们不应该局限于单一的方法或工具。正如本文所展示的,多样的交流策略不仅能够提供多角度的理解,还能增强信息的吸收和记忆。通过综合运用这些工具,我们能够使复杂的科技知识更加普及,让更多的人享受到科学带来的认知升级。
这篇关于科普如何做到既专业又易懂?这五种方法值得一试的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





