模块三：二分——153.寻找旋转排序数组中的最小值

本文主要是介绍模块三：二分——153.寻找旋转排序数组中的最小值，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目描述

题目链接：153.寻找旋转排序数组中的最小值

根据题目的要求时间复杂度为O(log N)可知需要使用二分查找。

算法原理

解法一：暴力查找

遍历数组一遍，寻找数组最小值并返回，时间复杂度为O(N)，因为需要遍历数组一遍，与本题要求不符，但是可以AC
PS：写这个解法的原因是因为我们最好想也最好写的解法就是暴力解法，经验不足的话都是靠暴力解法来做题的，搞懂了暴力解法之后，我们再去根据所学的算法和经验，借助画图，根据题目要求来优化我们的暴力解法，会让我们的基础比较扎实。

解法二：二分查找

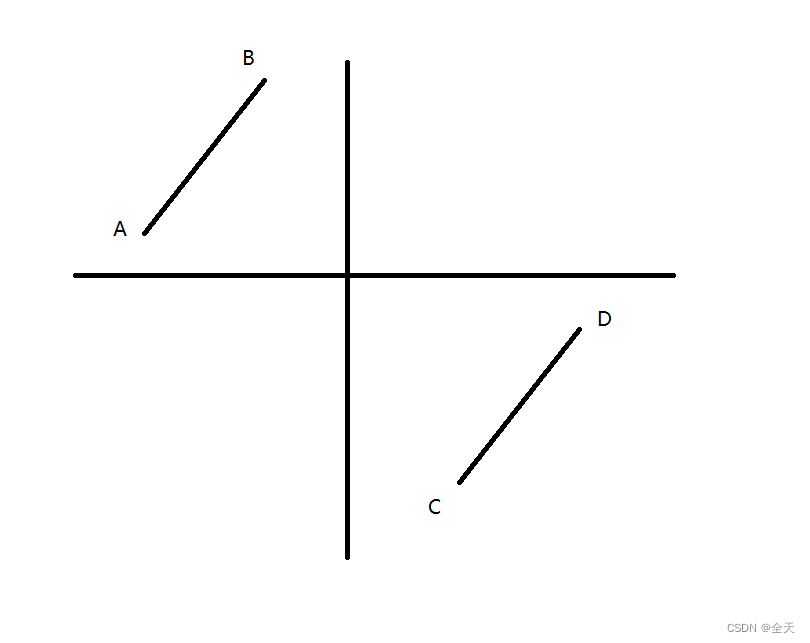
⼆分的本质：找到⼀个判断标准，使得查找区间能够⼀分为⼆。（二段性）
我们可以把数组划分成两部分，其中C点就是我们要的答案。通过图像我们可以发现， [A，B] 区间内的点都是严格⼤于 D 点的值的， C 点的值是严格⼩于 D 点的值的。但是当 [C，D] 区间只有⼀个元素的时候， C 点的值是可能等于 D 点的值的。
因此，初始化左右两个指针 left ， right ：然后根据 mid 的落点，我们可以这样划分下⼀次查询的区间：

• 当 mid 在 [A，B] 区间的时候，也就是 mid 位置的值严格⼤于 D 点的值，下⼀次查询区间在 [mid + 1，right]上；
• 当 mid 在 [C，D] 区间的时候，也就是 mid 位置的值严格⼩于等于 D 点的值，下次查询区间在 [left，mid] 上。
• 当区间⻓度变成 1 的时候，就是我们要找的结果。

疑问

请问可以选择A点作为参照物吗？大家可以想一想
答案放在解法二的C++代码部分解答。

代码实现

解法一：暴力查找

class Solution {
public:int findMin(vector<int>& nums) {int ret = INT_MAX;for(int i = 0;i < nums.size();++i){ret = min(ret,nums[i]);}return ret;}
};

解法二：C++

class Solution {
public:int findMin(vector<int>& nums) {//根据二段性可以使用二分int left = 0,right = nums.size() - 1;if(nums[left] < nums[right])return nums[left];while(left < right){int mid = left + (right - left) / 2;//答案是可以的，但是需要写成if(nums[mid] >= nums[0])，因为//当left = mid的时候，即只有两个数的时候，我们会跑去AB部分找答案//这会导致部分用例无法通过if(nums[mid] > nums[nums.size() - 1])left = mid + 1;else right = mid;}return nums[left];}
};

Java

class Solution {public int findMin(int[] nums) {int left = 0, right = nums.length - 1;int x = nums[right]; // 标记⼀下最后⼀个位置的值while (left < right) {int mid = left + (right - left) / 2;if (nums[mid] > x)left = mid + 1;elseright = mid;}return nums[left];}
}

这篇关于模块三：二分——153.寻找旋转排序数组中的最小值的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---