第十五届蓝桥杯省赛第二场C/C++B组F题【狡兔k窟】题解（AC）

本文主要是介绍第十五届蓝桥杯省赛第二场C/C++B组F题【狡兔k窟】题解（AC），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

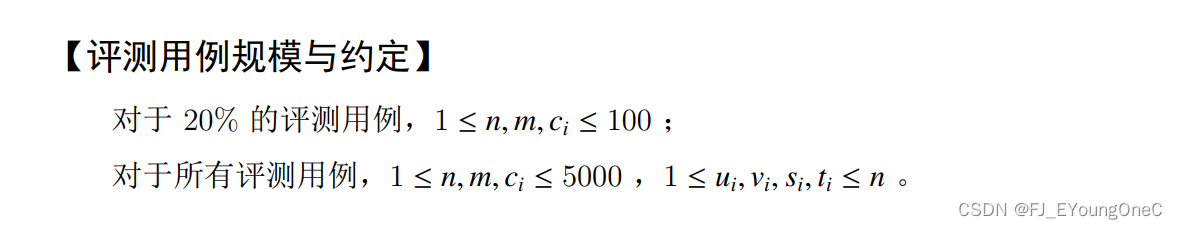
在这里插入图片描述

题意分析

有一个 $n$ 个点， $n - 1$ 条边的无向图，边权均为 $1$ 。

每个点隶属于一个集合，同一个集合的点可以互相传送。

给定 $m$ 个询问，求 $x, y$ 的最短距离。

最短路解法

步骤：

建图。
对于所有询问各跑一次最短路算法。

可选用的最短路算法：

Spfa，单次时间复杂度 $\sim O(n^2)$ ，总时间复杂度 $O(n^2) \sim O(n^3)$ 。
Dijkstra，单词时间复杂度 $O(n\log n)$ ，总时间复杂度 $O(n^2\log n)$ 。

01 BFS 解法

观察发现，本题仅存在边权为 $0$ 和 $1$ 的边，故上述最短路算法存在多余开销，我们考虑使用 BFS 算法进行求解，并使用 deque 进行维护。

进行扩展时，若是边权为 $0$ 的边，则放入队头，反之放入队尾。

最坏时，每条边均扩展 $n$ 个点，单次时间复杂度 $O(n^2)$ ，总时间复杂度 $O(n^3)$ 。

BFS 解法

样例如下：
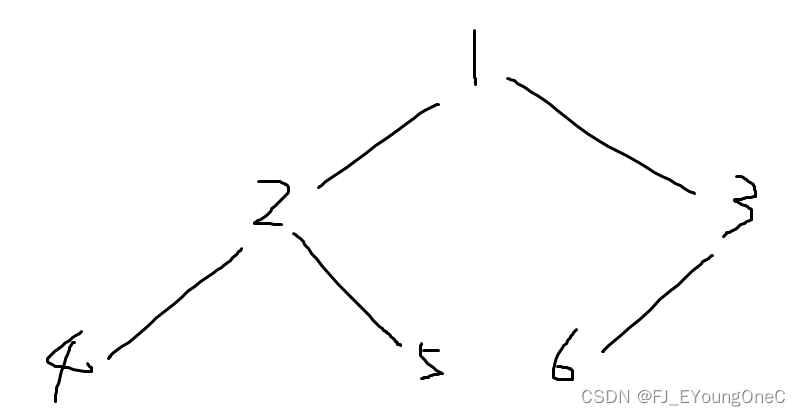
在这里插入图片描述
我们用虚线表示同一个组别中的连线。

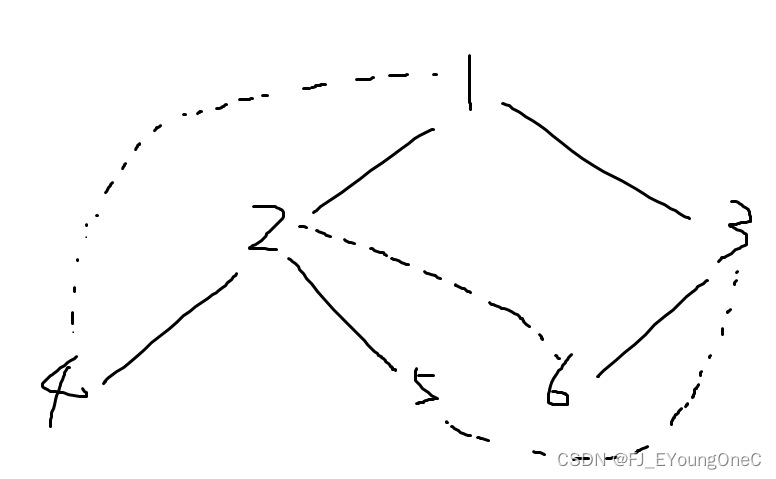
在这里插入图片描述

合并 $1, 4$ ：

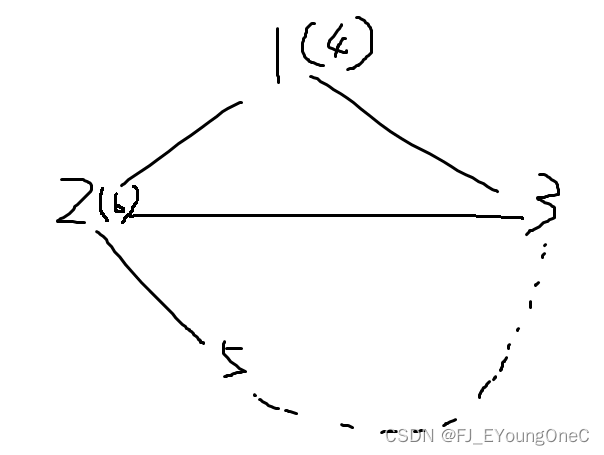
在这里插入图片描述
合并 $2, 6$ ：

在这里插入图片描述
合并 $3, 5$ ：

在这里插入图片描述
那么，在合并之后，当我们要算两个点之间的最短距离时，可以直接用 BFS 算法解决。

观察上图发现，因为组别内的点的边权为 $0$ ，所以我们可以将所有同一个组别的点进行合并，将点于点之间的最短路转换为组别于组别之间的最短路。

单词时间复杂度 $O (n)$ ，总时间复杂度 $O(n^2)$ 。

#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <queue>
#include <vector>using namespace std;const int N = 5e3 + 10, M = N * 4;int n, m;
int h[N], e[M], w[M], ne[M], idx;
int belong[N];
vector<int> g[N];
int dist[N];
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}void bfs(int u, int v)
{memset(dist, 0x3f, sizeof dist);memset(st, 0, sizeof st);dist[u] = 0;queue<int> q;q.push(u);while (q.size()){auto t = q.front();q.pop();for (int i = h[t]; ~i; i = ne[i] ){int j = e[i];if (dist[j] > dist[t] + w[i]){dist[j] = dist[t] + w[i];q.push(j);}}}cout << dist[v] << endl;
}int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin >> n >> m;memset(h, -1, sizeof h);for (int i = 1; i <= n; ++ i ){int x;cin >> x;belong[i] = x;g[x].push_back(i);}for (int i = 1; i < n; ++ i ){int a, b;cin >> a >> b;a = belong[a], b = belong[b];add(a, b, 1), add(b, a, 1);}while (m -- ){int a, b;cin >> a >> b;bfs(belong[a], belong[b]);}return 0;
}