本文主要是介绍安卓玩机工具推荐----MTK芯片 简单制作线刷包 备份分区 备份基带 去除锁类 推荐工具操作解析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

工具说明
在前面几期mtk芯片类玩机工具中解析过如何无官方固件从手机抽包 制作线刷包的步骤,类似的工具与操作有很多种。演示的只是本人片面的理解与一些步骤解析。mtk芯片机型抽包关键点在于..mt*****txt的分区地址段引导和 perloader临时分区引导。前面几期都是需要几个工具结合操作来制作线刷包。今天以另外一款工具演示如何方便简单 快速的制作mtk线刷包。
这款工具的优点在于不需要借助其他工具。即可自动读取当前芯片生成线刷包。包括mt*****.txt与preloader和其他手机分区和当前机型pgpt分区表。并且不需要转换格式。另外带免权限刷写 去除屏幕锁类 备份基带等等功能.当然机型芯片有区别。不可能涵盖支持所有mtk芯片的操作.懂得都懂。
同类博文;
安卓玩机工具推荐----MTK 高通芯片机型 免权限刷机 备份基带 去除锁类工具操作步骤解析_mtk刷机工具-CSDN博客
救砖刷机------MTK芯片类线刷 救砖 免授权的一些操作步骤与工具解析【一】_刷机救砖工具-CSDN博客
玩机进阶教程----MTK芯片读写分区 备份分区 恢复分区 制作线刷包 从0开始 工具操作解析【三】_mtk线刷包只制作-CSDN博客
安卓玩机工具推荐----MTK芯片读写分区 备份分区 恢复分区 制作线刷包 工具操作解析【二】_mtk工具-CSDN博客
安卓玩机工具推荐----MTK芯片读写分区 备份分区 恢复分区 制作线刷包 工具操作解析【一】_安卓recovery分区备份-CSDN博客
选项说明:
red GPT:此功能允许读取设备的 分区表
backup:备份选择好的分区
erase:檫除选择好的分区
flash:刷写选择的固件线刷包或者读取出来的分区替换的分区
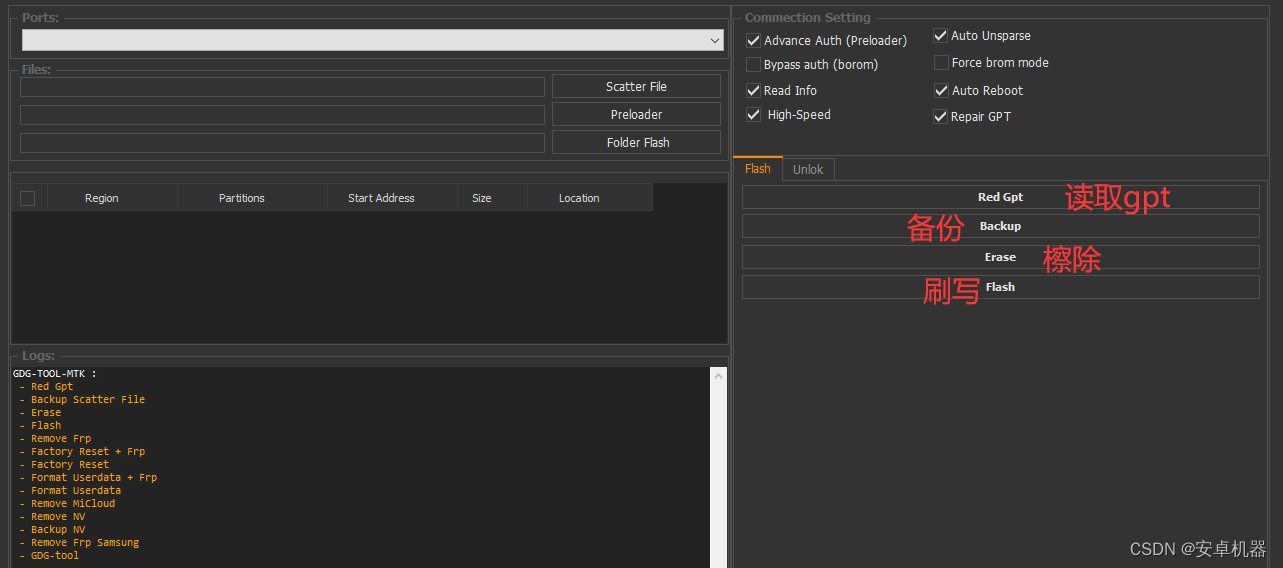

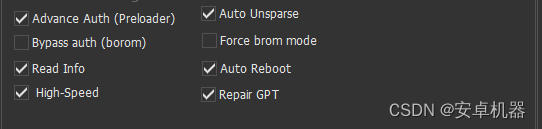
以上只是对各个选项做个释义。那么对于默认的选项。自动preloader . 免授权.读信息.高速.自动制作txt、自动重启.修复gpt,正常默认即可。如果需要授权 勾选bypass auth选项。
****************************************************************************************************
演示如何简单快速制作线刷包
演示之前的驱动安装 联机按键等等在不做说明。可以参阅以往博文。这些都是基础常识。以红米9A mtk6765作为演示机型。这机型正常读写是需要授权的。懂的都懂。点击工具的red gpt按钮。然后手机关机状态下。按住音量上键链接数据线触发联机端口。
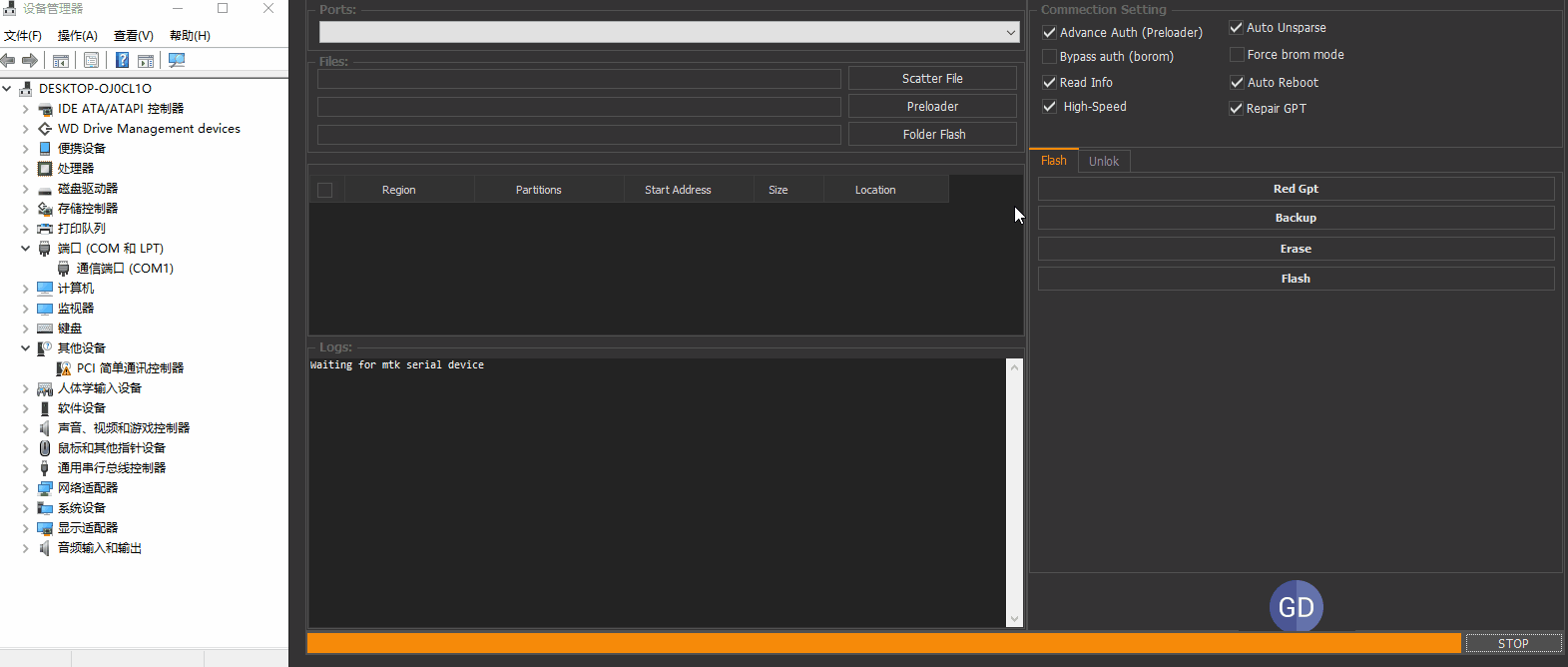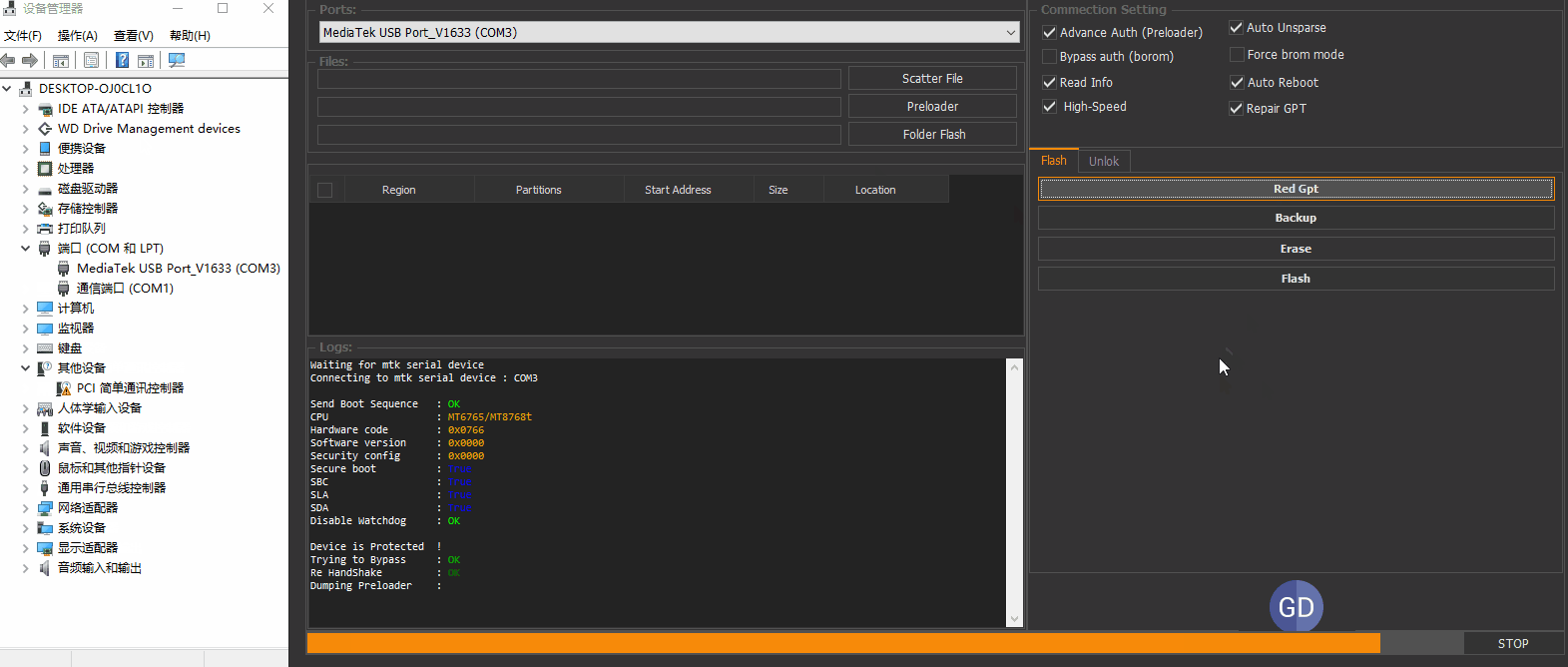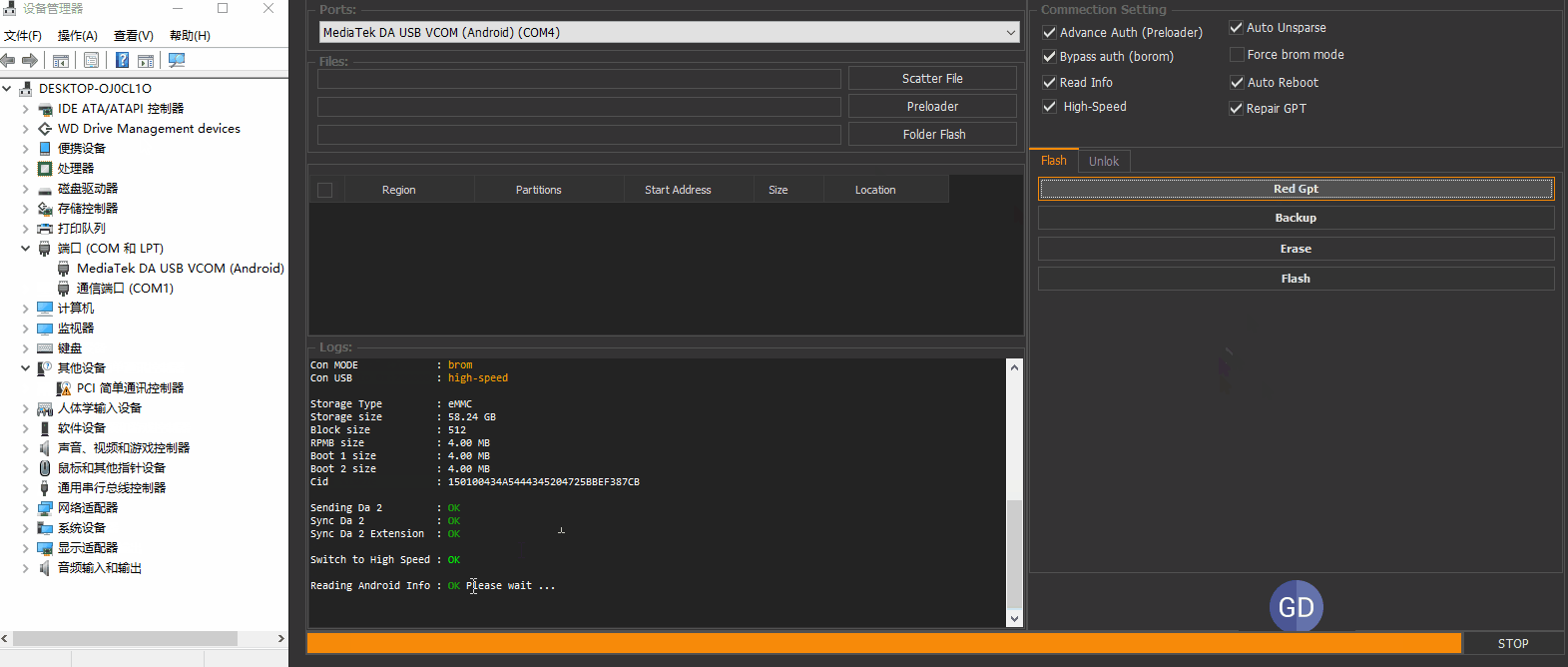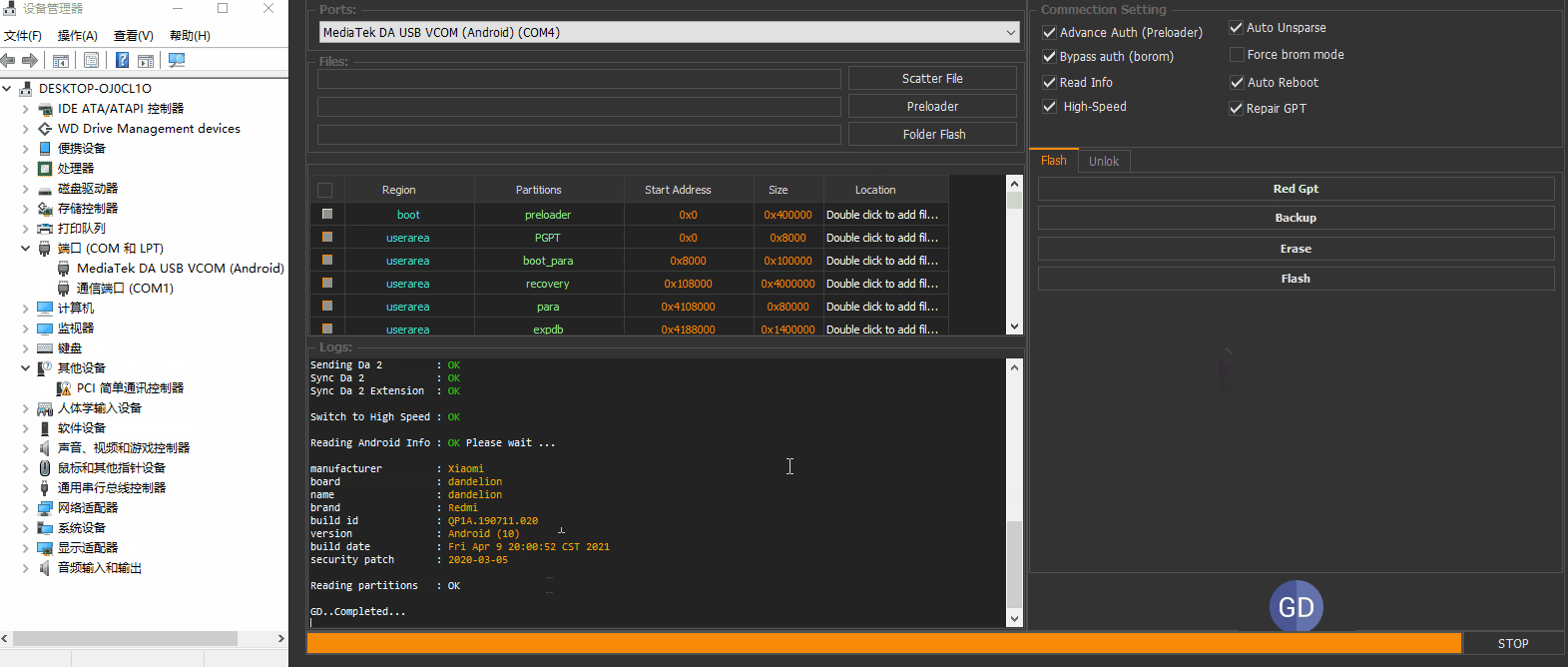
通过以上动画我们可以看到工具已经读取当前手机的机型分区。此时我们点击左边的分区选项即可备份。方便演示我们只勾选几个小分区。

勾选自己选择的分区后点击工具的备份按钮。即可备份。通过演示可以看到自动备份了分区和自动制作好了 MT6765_Android_Scatter.txt引导和preloader分区。是不是相对于其他工具来说方便简单哦。当然你可能需要修改下MT6765_Android_Scatter.txt下的脚本。将有些不需要刷写的分区修改为不刷写。这类操作可以对比修改。
备份nv分区
nv分区就是手机的基带分区。避免格机脚本或者误檫除全分区导致的基带丢失问题。需要备份基带分区。操作也是一样。点击选项区的backup nv选项。会让你选择备份分区存储目录。选择好后联机备份

可以很清楚的看到。联机后读取并且备份了基带有关的几个分区 .
其他选项:
至于恢复出厂 格式化用户数据分区等等之类的操作不在演示。性质都是一样的。操作无区别。只要驱动装好。联机正常。操作得心应手。frp是谷歌账号。国内一般不操作这个。至于格式化data。只要你有屏幕锁类的 操作完都会清除掉。
刷写免权限操作
9A 选好引导和固件文件夹。进行联机操作。方便操作只演示logo和recovery分区的刷写
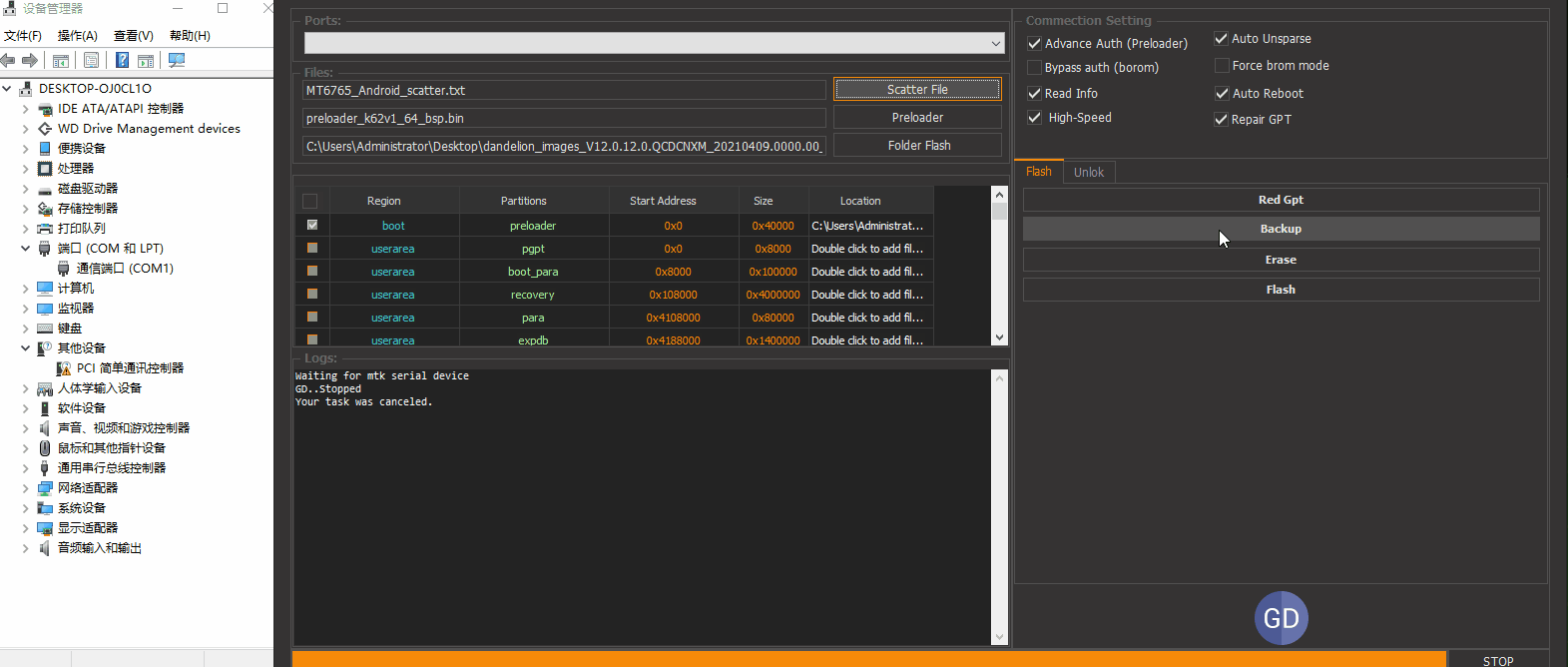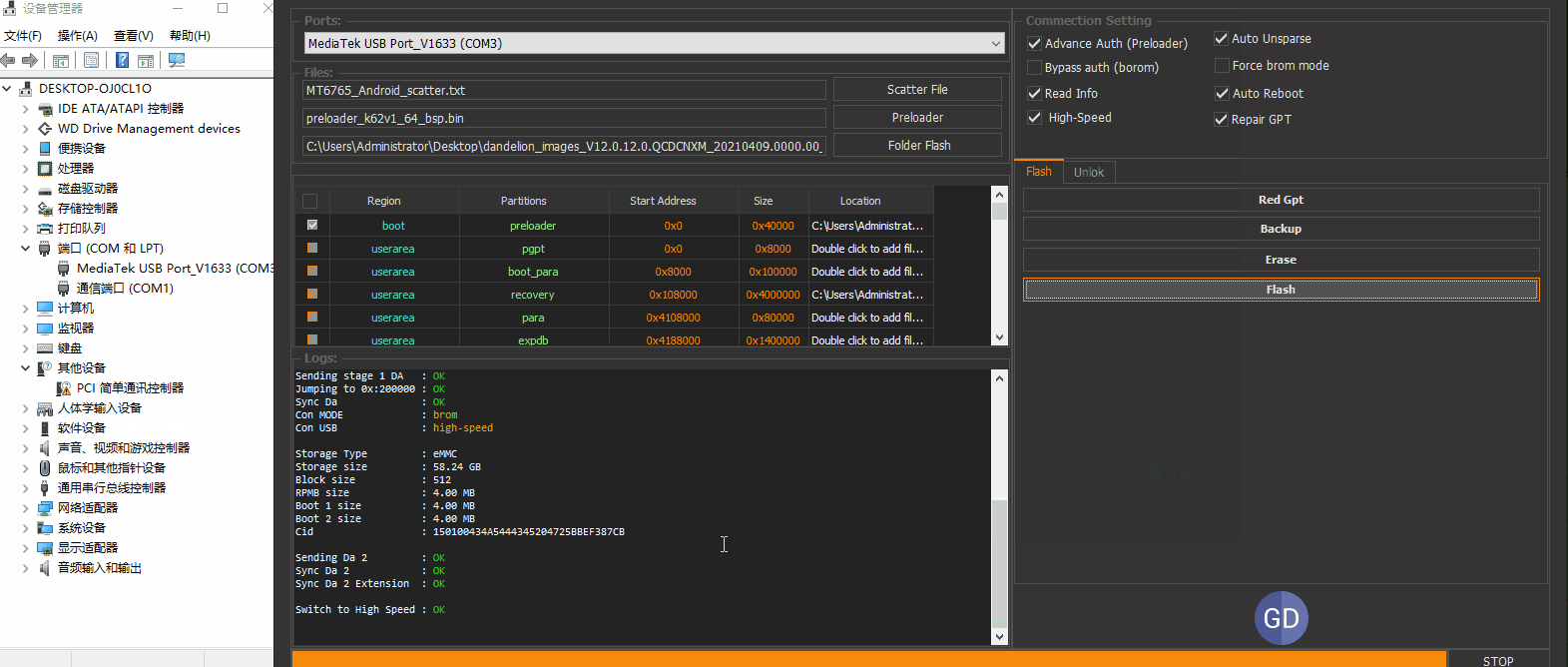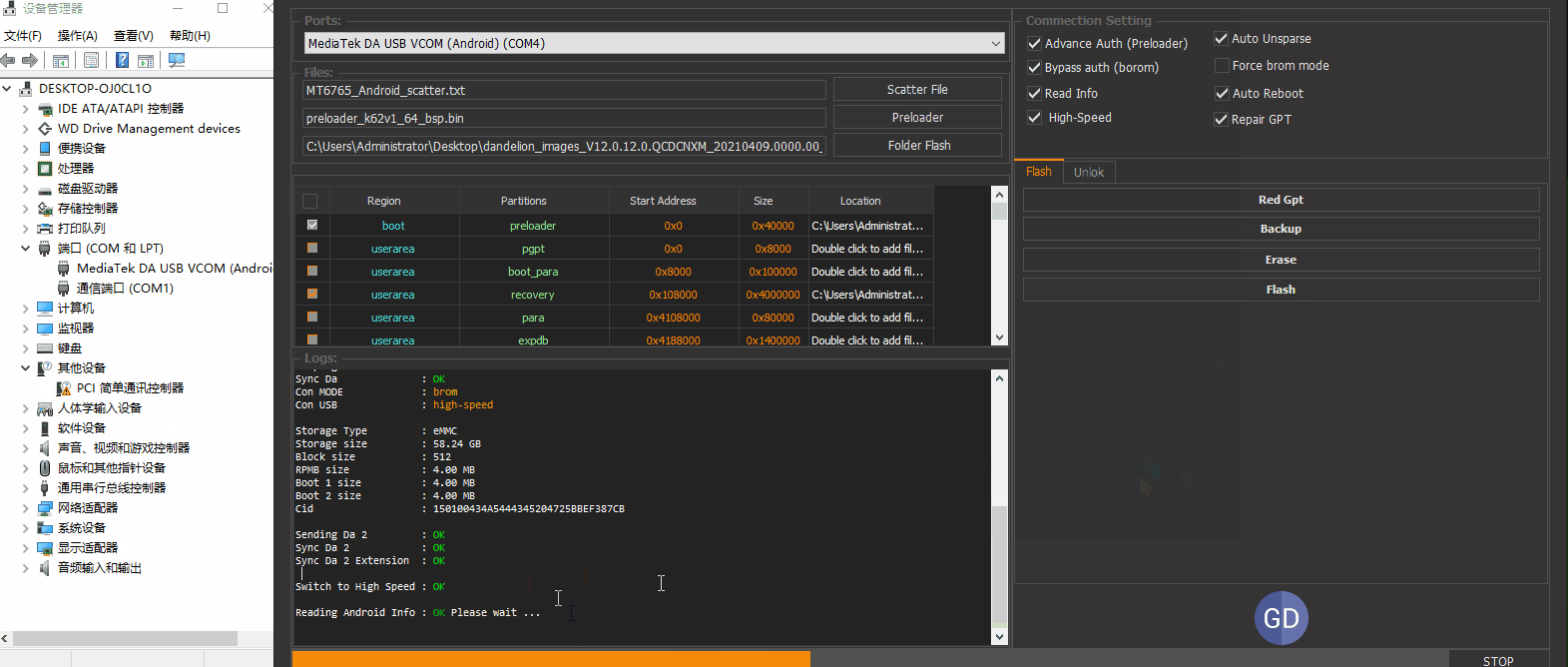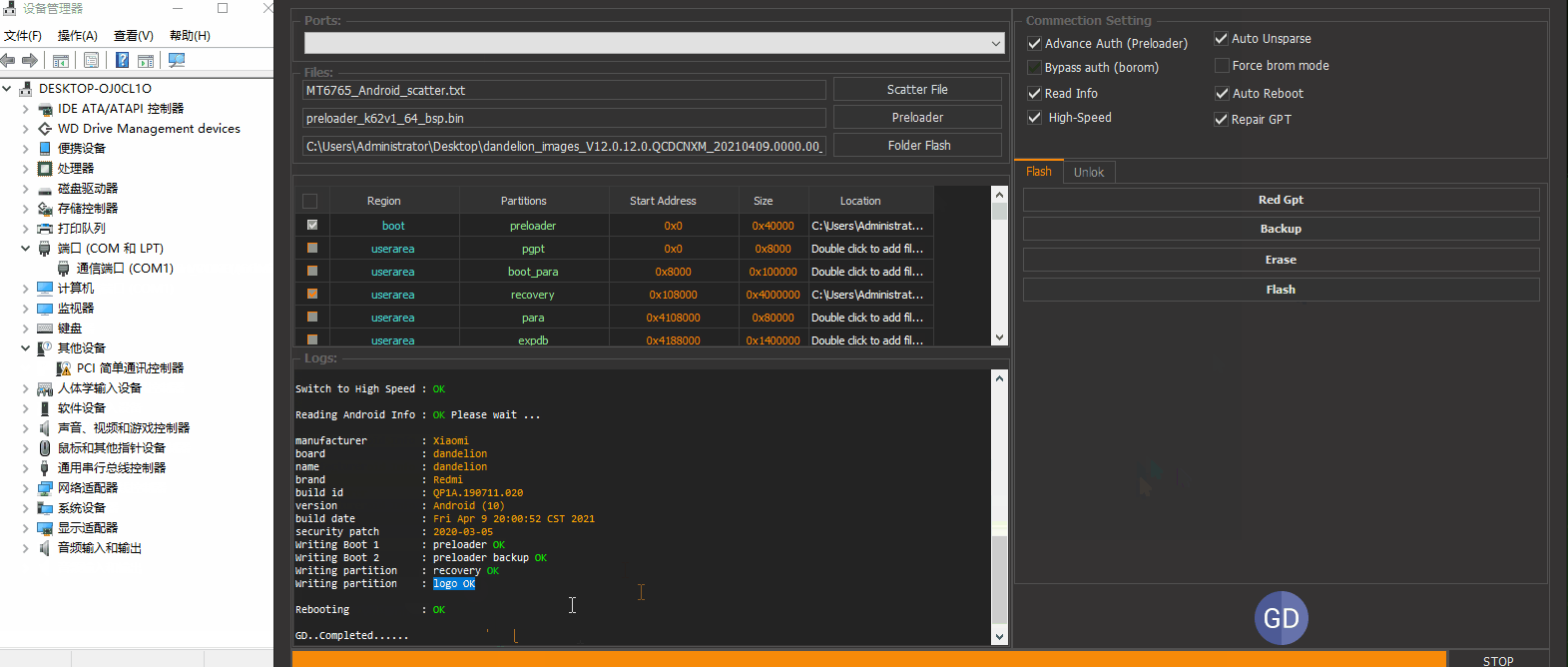
可以看到两个分区写入ok。
工具下载:
总结:
在好的教程和工具最终还是在于使用者。对于基础常识和操作能力薄弱的友友需要谨慎。因为有些分区操作是不可逆的。失误会导致手机分区受损。严重会进不去系统甚至黑屏。另外机型和版本较多。不一定工具支持所有的机型。另外也要了解mt的BROM模式META模式和mt刷机加载的DA文件等等相关常识。这些都与工具操作有一定的关联.

这篇关于安卓玩机工具推荐----MTK芯片 简单制作线刷包 备份分区 备份基带 去除锁类 推荐工具操作解析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




