Hdu3360 National Treasures【最小点覆盖】

本文主要是介绍Hdu3360 National Treasures【最小点覆盖】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

National Treasures

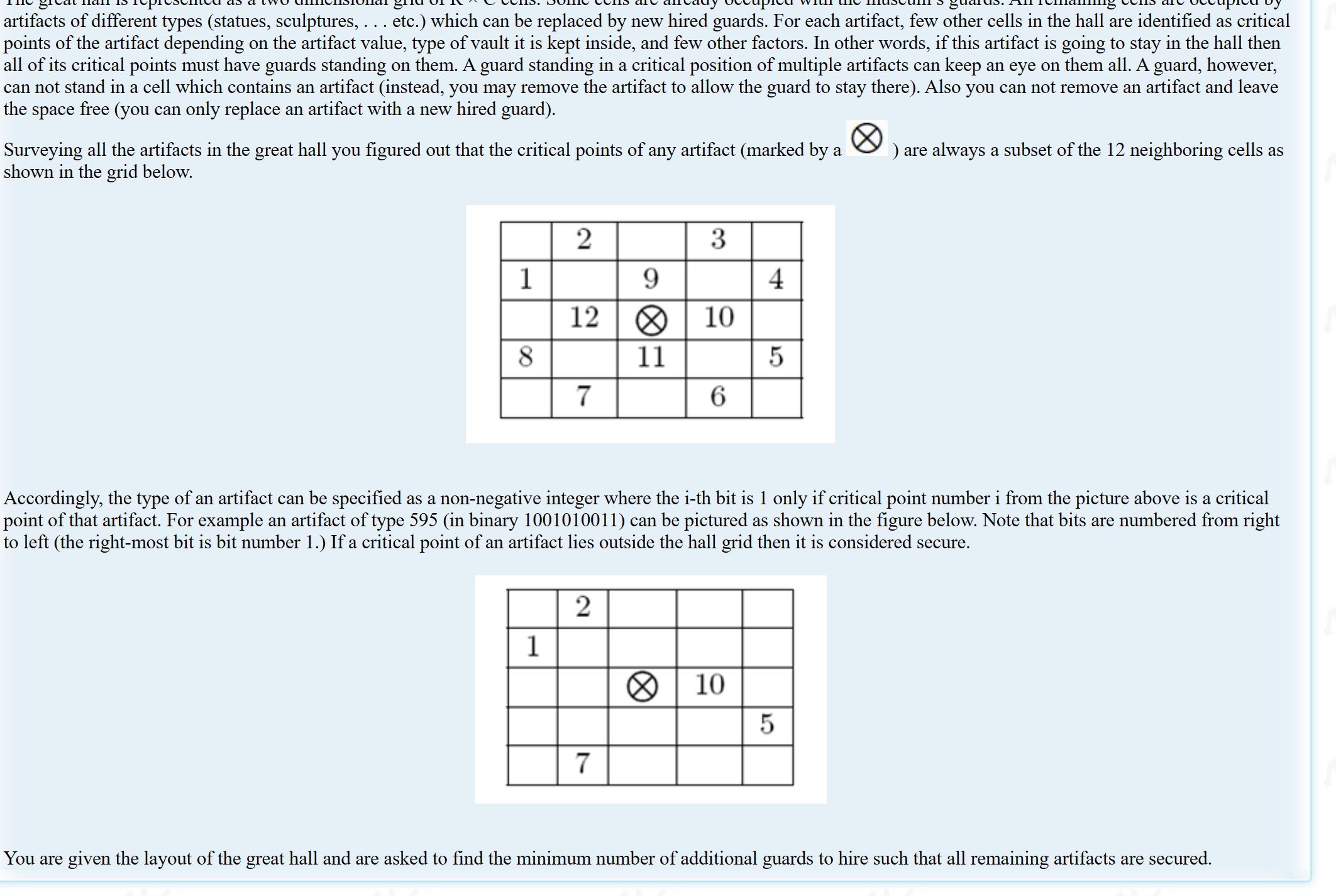
题意

一个 $\times m$ 的网格图，有若干个宝物，每个宝物有可能有一些关键位置（如上图的宝物，拥有 $12$ 种关键位置中的 $1, 2, 5, 7, 10$ ）
对于某个宝物，必须把它的所有关键位置都放置一个卫兵，网格图的某些位置可能已经有了卫兵

现在要求出为了满足要求，最少需要放置多少个卫兵？也可以将某个宝物换成卫兵，但是不能只删除宝物而不放卫兵

思路

我们将某个宝物与它的所有关键点连边，表示一种守护关系（如果这个位置已经有卫兵，那么不连边），那么对于最后形成的图，问题就转化成了：选择一些点，覆盖所有边（守护关系），也即是最小点覆盖

注意到如果一个宝物被换成了卫兵，那么等价于它的所有关键点都被覆盖了（所有守护关系都满足）

因此直接二分图跑最大匹配即可

#include<bits/stdc++.h>
#define fore(i,l,r)	for(int i=(int)(l);i<(int)(r);++i)
#define fi first
#define se second
#define endl '\n'
#define ull unsigned long long
#define ALL(v) v.begin(), v.end()
#define Debug(x, ed) std::cerr << #x << " = " << x << ed;const int INF=0x3f3f3f3f;
const long long INFLL=1e18;typedef long long ll;const int N = 55;int n, m;
int a[N][N]; //地图
int mv[12][2] = { //卫兵{-1, -2}, {-2, -1}, {-2, 1},{-1, 2}, {1, 2}, {2, 1},{2, -1}, {1, -2}, {-1, 0},{0, 1}, {1, 0}, {0, -1}
};std::vector<std::vector<int>> g;
std::vector<int> match;
std::vector<bool> used;bool in(int x, int y){return x >= 0 && x < n && y >= 0 && y < m;
}bool dfs(int u){for(auto v : g[u])if(!used[v]){used[v] = true;if(match[v] == -1 || dfs(match[v])){match[v] = u;return true;}}return false;
}int main(){std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);int test = 0;while(std::cin >> n >> m && n && m){fore(i, 0, n)fore(j, 0, m)std::cin >> a[i][j];g.assign(n * m + 5, std::vector<int>());match.assign(n * m + 5, -1);fore(i, 0, n)fore(j, 0, m){if(a[i][j] == -1) continue;fore(k, 0, 12)if(a[i][j] >> k & 1){int x = i + mv[k][0], y = j + mv[k][1];if(in(x, y) && a[x][y] != -1){g[x * m + y].push_back(i * m + j);g[i * m + j].push_back(x * m + y);}}}int cnt = 0;fore(i, 0, n * m){used.assign(n * m + 5, false);cnt += dfs(i);}std::cout << ++test << ". " << cnt / 2 << endl;}return 0;
}