6.6 完数（project） educoder项目实训

本文主要是介绍6.6 完数（project） educoder项目实训，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前言

        在最近的Python课上，做到这样一个“有趣”的作业，求得前n个完数，并输出其与其真约数的约数的加和式子，刚开始没怎么在意这个题，想着不就是做过好几遍了的语言基础练习题嘛，但是接下来的几小时没想到都在肝这个，具体原因请继续往下看

第一关

到现在为止一切安好，就是基础语言练习题而已，秒了

代码

import mathdef f(n):r = 1for i in range(2, int(math.sqrt(n))+1):if(n % i == 0):r += (i + n / i)return r == ncnt,num = 0,2
x = int(input())
while cnt < x:num += 1if f(num):fac = [i for i in range(1,num) if num%i == 0]s = str(num) + '='for i in fac:s += str(i) + '+'print(s.rstrip('+'))cnt += 1

第二关

        我一看题目完全没变，寻思怎么能出一样的题目呢？？然后直接ctrl c + ctrl v开始评测，正当我沉浸在题目秒了的喜悦中，我发现了这样一个东西

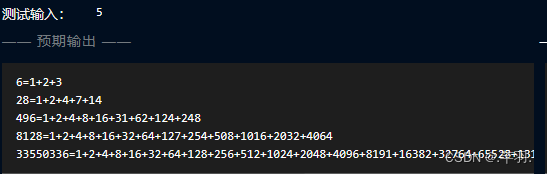
然后不出所料，没能在20s内完成任务，TLE了

于是我开始在网上搜寻有关完全数的数学知识，很快就找到了欧拉提出的完全数获得公式：

如果p是质数，且2^p-1也是质数，那么(2^p-1)* 2^(p-1)便是一个完全数。

用这样的办法改进一下代码还是很easy的，不久就得到了这样一个崭新出厂的代码

代码

import mathdef is_prime(n):for i in range(2, int(math.sqrt(n))+1):if(n % i == 0):return Falsereturn Truecnt, num = 0, 2
x = int(input())
while cnt < x:if is_prime(num) and is_prime(2 ** num - 1):a = 2 ** (num-1) * (2 ** num - 1)s = str(a) + '='fac = [1]for i in range(2,2 ** num - 1):if(a % i == 0):fac.append(i)fac.append(a // i)fac.sort()print(s + str(fac).replace(', ','+').lstrip('[').rstrip(']'))cnt += 1num += 1

ac题目总是让人心情愉悦的，所以我顺势点开了下一关

 第三关

这回我学聪明了，先去看了看测试集，虽然有心理预警，但仍然吓了一跳

阶段1

当我看到这个9心里已经凉了一半了，另一半是当我cv提交测试没过的时候彻底凉透的，那么很显然需要一些数学上的优化，此时我想到如果单独将素数罗列出来，可以节省一次素性检验，只需检验 (2 ^ n) -1 是否也为素数即可，但是这样节约的时间仍然不足以让题目完全ac。

阶段2

此时我发现我做了太多的除法和模运算，对于大数的计算是很费时间的，于是我开始观察约数的序列，得到这样一个事实：除了 (2^n)-1 ， 完数a的其他约数都是 2 ^ n的形式，于是我想到可以将他们特殊处理，这里把1也放进来是为了防止完数a本身也进入列表，此时已经可以ac题目了。

阶段3

但是150s的运行时间让我觉得下一关肯定也过不了，不如所性继续优化，于是我想起一种更快速的，类似于筛法的素性检验算法，更换了素性检验算法后时间降至50s左右，此时我再一次沉浸在喜悦之中

代码

import mathdef is_prime(n):if n <= 1:return Falseif n <= 3:return Trueif n % 2 == 0 or n % 3 == 0:return Falsei = 5while i * i <= n:if n % i == 0 or n % (i + 2) == 0:return Falsei += 6return Truecnt = 0
prime = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61]
index = 0
x = int(input())
while cnt < x:# 欧拉的完数公式 ： 如果 n 和  (2**n -1) 同为素数 则 (2^(n-1)) * ((2^n) -1)为完数if is_prime(2 ** prime[index] - 1):a = 2 ** (prime[index]-1) * (2 ** prime[index] - 1)s = str(a) + '='# 寻找约数fac = [1]for i in range(1, prime[index]):t = 2 ** ifac.append(t)fac.append(a // t)fac.sort()print(s + str(fac).replace(', ', '+').lstrip('[').rstrip(']'))cnt += 1index += 1

第四关

        此时内心想法其实是：第三关运行时间给了200s，第四关应该给的更多吧。但点进去一看，居然只有20s？？！！而且这个测试集我&*%……&%￥#%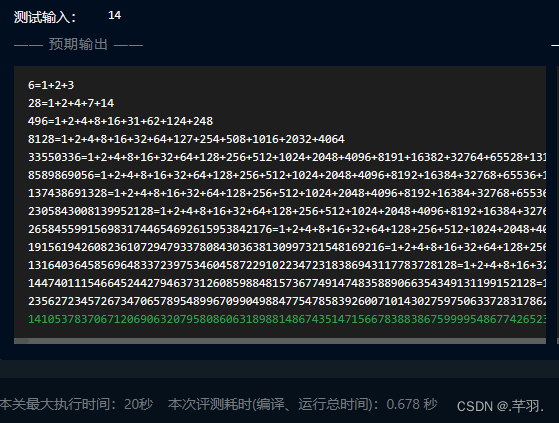

压抑住爆粗口的冲动，接着想优化的方法。

我先想着 2^(n)-1这样的数有没有什么特殊性质，然后发现这个东西叫做梅森数，而且发现，对于梅森数有着一种特殊的素性检验法，叫做lucas-lehmer检验法​​​​​​，这真是解决了大问题，然后我又发现，我所需要的素数序列，靠人力最多写到一百多，就要花很多时间在手动计算素数上了，这很不符合程序设计的理念（我要是自己算要程序干嘛！！！）那么曾经学过一种得到素数序列的犯法叫做欧拉筛法（也称线性筛法）就派上用场了，O（n）的时间复杂度太香了！！基本不会挤占我的运行时间。除此之外，我又将乘除法和阶乘等运算换成了对应的位运算，更尽可能的加速程序的运行，功夫不负有心人，终于解决了这样的问题，并且运行时间不到1s！！！（跨越性进步好耶！）

代码

import math# 欧拉筛法获取小于r的素数列表
# 可以节省对每个n进行素性检验的过程，避免更多的计算
def oula(r):# 全部初始化为0prime = [0 for i in range(r+1)]# 存放素数common = []for i in range(2, r+1):if prime[i] == 0:common.append(i)for j in common:if i*j > r:breakprime[i*j] = 1#将重复筛选剔除if i % j == 0:breakreturn common'''
卢卡斯-莱默素性检验法
令梅森数 M[p]=2^p-1作为检验对象,
定义数列 L[n]:L[n-1] ^ 2 - 2,n>0. 
这个数列的开始几项是4,14,194,37634,1416317954……
那么M[p]是质数当且仅当L[p-2] ≡ 0 (mod M[p])
否则Mp是合数。sp−2模Mp的余数叫做Mp的卢卡斯－莱默余数。
'''
def primality(N, M):if N == 2:return Trues = 4for i in range(N-2):s = (s * s - 2) % Mreturn s == 0cnt,index = 0,0
prime = oula(2000)
# 可以刚好得到完数的 n，虽然可以节省一定时间，但通过答案倒推过程不符合程序设计的合理性
# res = [2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279]
x = int(input())
while cnt < x:# 欧拉的完数公式 ： 如果 n 和  (2**n -1) 同为素数 则 (2^(n-1)) * ((2^n) -1)为完数m = (1 << prime[index])- 1if primality(prime[index],m):a = m << (prime[index]- 1)s = str(a) + '=''''寻找约数观察数据不难得知,除了m,a其余的约数都是 2 ^ n 形式,这里初始化将1也放进来是避免 a 本身进入列表中那么我们通过这个结论，可以不再使用试除法获取约数列表节省更多的时间'''fac = [1,m,(m+1)>>1]num1 = 2num2 = a >> 1'''误区记录：insert具有O(n)的时间复杂度，相比append的O(1)，虽然节省了排序的O(nlogn)，但数据大时并不更省时。for i in range(1, factors[index]-1):fac.insert(i+2,num2)fac.insert(i,num1)num1 <<= 1num2 >>= 1'''for i in range(1, prime[index]-1):fac.append(num1)fac.append(num2)num1 <<= 1num2 >>= 1fac.sort()print(s + str(fac).replace(', ', '+').lstrip('[').rstrip(']'))cnt += 1index += 1

总结

        一个小小完数，居然涉及如此广泛的数论知识，深刻提醒我数学在计算机领域的运用确实是十分广泛的，学习算法的路上，数学一定是一大助力。

这篇关于6.6 完数（project） educoder项目实训的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---