本文主要是介绍后缀数组四·重复旋律4,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
我们知道一个音乐旋律被表示为长度为 N 的数构成的数列。
我们把一段旋律称为(k,l)-重复的,如果它满足由一个长度为l的字符串重复了k次组成。 如旋律abaabaabaaba是(4,3)重复的,因为它由aba重复4次组成。
小Hi想知道一部作品中k最大的(k,l)-重复旋律。
输入
一行一个仅包含小写字母的字符串。字符串长度不超过 100000。
输出
一行一个整数,表示答案k。
babbabaabaabaabab
4解法提示:
这次的问题是重复次数最多的连续字串。
先降低难度,不如考虑如何解决如何求一个串的最大重复次数。
比如说串abababab,既可以是(1,8),也可以是(2,4),最大的是(4,2)。
假如说我们枚举一个可能的循环节长度l(或者k),能不能快速判断这个l是否合法呢?
似乎是求原串和原串去掉前l个字符后两个串的LCP(最长公共前缀),如果能完全匹配上,就满足!
比如abababab,检验是否是(2,4),就拿abababab和ababab求LCP。
值得一提的是,利用height数组可以快速求出我们需要的LCP。例如abababab的height数组如下:
| suffix | sa | height |
|---|---|---|
| ab | 7 | 0 |
| abab | 5 | 2 |
| ababab | 3 | 4 |
| abababab | 1 | 6 |
| b | 8 | 0 |
| bab | 6 | 1 |
| babab | 4 | 3 |
| bababab | 2 | 5 |
如果我们要求某两个后缀的LCP,只要求它们中间的一段height数组的最小值即可。例如abababab和ababab的LCP就是[6]这段的最小值,即6;bab和bababab的LCP就是[3, 5]这段的最小值,即3;ab和babab的LCP就是[2, 4, 6, 0, 1, 3]这段的最小值,即0。
这个求height数组某一段最小值的问题,恰好是之前讲过的[RMQ问题],可以通过O(NlogN)的预处理达到O(1),处理单次询问;当然使用线段树等数据结构也是可以的,单次询问O(logN)。
明白了。回到原问题,那我们肯定是要先枚举(k,l)中的这个l,再枚举起始位置i,计算Suffix(i)和Suffix(i+l)的LCP,记作lcp(l, i),那么k(l, i)就等于lcp(l,i)/l + 1。对于所有的循环节长度l和起始位置i,最大的k(l, i)就是答案。
不过本题还是有进一步优化的空间。对于确定的l,我们不用枚举所有的起始位置i,而只枚举i是l的整数倍的情况。如果最优串的开始位置恰好在l的倍数上,那我们找到的最大的k就是正确答案。
即使不是,问题也会太糟糕,假如说最优串位置在x,可以想象我们会枚举到x之后的一个最近位置p,p是l的倍数。并且我们计算出了Suffix(p)和Suffix(p+l)的LCP,lcp(l, p)那么此时的k(l, p)=lcp(l, p)/l+1。
对于被我们略过的k(l, p-1), k(l, p-2) ... k(l, p-l+1),它们的上限是k(l, p)+1。
因为它们的起始位置距离p不超过l,所以最多比Suffix(p)增加一个循环节。
其次,如果k(l, p-1), k(l, p-2) ... k(l, p-l+1)中有一个的值是k(l, p)+1的话,那么k(l, p - l + lcp(l, p) mod l)一定等于k(l, p)+1。(mod是取余运算)
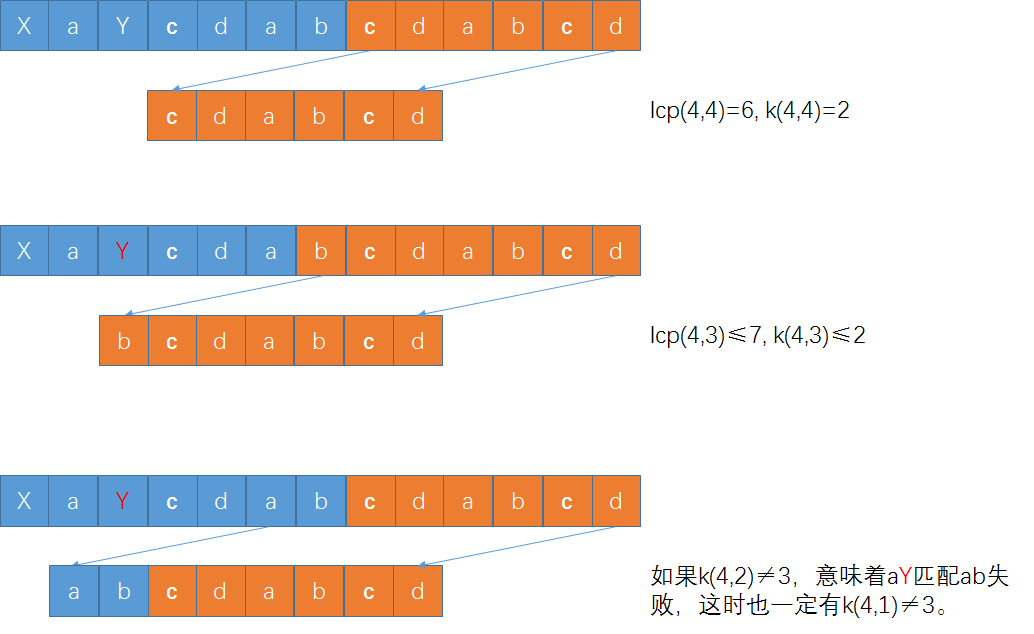
举个例子,比如串XaYcdabcdabcd(XY各代表一个不确定的字符,具体代表的字符会影响最后答案,我们后面会分析到),当我们考虑l=4的时候,第一次枚举p=4的起始位置,会求出cdabcdabcd和cdabcd的lcp(4, 4)=6,k(4, 4)=2。根据上面的论断,只有当k(l, p - l + lcp(l, p) mod l)=k(4, 4 - 4 + 6 mod 4)=k(4, 2)=3时,k(4, 1), k(4, 2)和k(4, 3)中才会有3。首先我们可以判断k(4, 3)一定不可能等于3,因为无论Y是哪个字符,Ycdabcdabcd和bcdabcd的LCP即lcp(4, 3)最大是7,不到8。 其次如果k(4, 2) ≠ 3,那么k(4, 1)也没戏。因为如果k(4, 2) ≠ 3,说明aY和ab匹配不上,这时无论X是哪个字符,XaY和dab匹配不上,lcp(4, 1) < l,k(4, 1) = 1。
哦,我有点明白了。k(l, p - l + lcp(l, p) mod l)是一个分界线,右边的值因为LCP不够大,一定不能增加一个循环节。并且如果k(l, p - l + lcp(l, p) mod l)没有增加循环节的话,说明[p - l + lcp(l, p) mod l, p]这段中间匹配出错,左边的lcp也跟着雪崩,更不可能增加循环节了。
枚举完l后枚举开始位置的时间复杂度是O(n/l)的,所以总复杂度是O(n/1)+O(n/2)+O(n/3)...这个是一个经典的求和,总复杂度是O(nlogn)的。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <string>
#include <algorithm>
using namespace std;//FILE *stream;
string s;
int n;
const int N = 100000 + 50;
int SA[N];//后缀数组,保存排序后后缀字符串的开头位置,本身下标对应名次
int RANK[N];//名次数组,保存排序后后缀字符串名次,本身下标对应字符串开头位置
int HEIGHT[N];//排名相邻的两个后缀的最长公共前缀
int wa[N], wb[N], wss[N], wv[N];int cmp(int *r, int a, int b, int l)
{return (r[a] == r[b]) && (r[a + l] == r[b + l]);
}void getSA(string r, int *sa, int n, int m)//r为初始输入,可以对应改为字符串数组,sa[]为后缀数组,n为输入个数+1,m为输入中的最大值,字符的话可以对应改为ascii码最大值
{int i, j, p, *x = wa, *y = wb, *t;for (i = 0; i<m; i++) wss[i] = 0;for (i = 0; i<n; i++) wss[x[i] = r[i]]++;for (i = 1; i<m; i++) wss[i] += wss[i - 1];for (i = n - 1; i >= 0; i--) sa[--wss[x[i]]] = i;for (j = 1, p = 1; p<n; j *= 2, m = p){for (p = 0, i = n - j; i<n; i++) y[p++] = i;for (i = 0; i<n; i++) if (sa[i] >= j) y[p++] = sa[i] - j;for (i = 0; i<n; i++) wv[i] = x[y[i]];for (i = 0; i<m; i++) wss[i] = 0;for (i = 0; i<n; i++) wss[wv[i]]++;for (i = 1; i<m; i++) wss[i] += wss[i - 1];for (i = n - 1; i >= 0; i--) sa[--wss[wv[i]]] = y[i]; //基数排序部分for (t = x, x = y, y = t, p = 1, x[sa[0]] = 0, i = 1; i<n; i++)x[sa[i]] = cmp(y, sa[i - 1], sa[i], j) ? p - 1 : p++;}
}void getHeight(string r, int n)
{int i, j, k = 0;for (i = 0; i <= n; i++) RANK[SA[i]] = i;//将RANK从0开始标记for (i = 0; i < n; HEIGHT[RANK[i++]] = k)for (k ? k-- : 0, j = SA[RANK[i] - 1]; r[i + k] == r[j + k]; k++);
}//输入aa[0]-aa[n-1]
//getSA(aa,SA,n+1,105); //注:此处计算出的为SA[1]-SA[n],而且每个SA值表示的是下标,从0-n-1
//getHeight(aa,n); //注:此处计算出的为HEIGHT[1]-HEIGHT[n]int lcp[N][32];//lcp[index][len]保存从index开始,2^len范围内HEIGHT[]中的最小值void init(int n)//二分法
{for (int i = 1; i <= n; i++)lcp[i][0] = HEIGHT[i];for (int i = 1; (1 << i) <= n; i++)for (int j = 1; j + (1 << i) - 1 <= n; j++)lcp[j][i] = min(lcp[j][i - 1], lcp[j + (1 << i - 1)][i - 1]);
}int LCP(int a, int b) //计算a,b下标开始两个字符串的最长公共前缀
{a--; b--;int l = min(RANK[a], RANK[b]) + 1, r = max(RANK[a], RANK[b]);int len = r - l + 1, i;for (i = 0; (1 << i) <= len; i++);i--;return min(lcp[l][i], lcp[r - (1 << i) + 1][i]);//计算起始位的lcp和包含最后一位HEIGHT的lcp
}void solve()
{int ans = 0;for (int L = 1; L <= n; ++L){for (int i = 1; i + L <= n; i += L){int R = LCP(i, i + L);ans = max(ans, R / L + 1);if (i >= L - R%L)ans = max(LCP(i - L + R%L, i + R%L ) / L + 1, ans);}}cout << ans << endl;
}int main()
{//freopen_s(&stream, "in.txt", "r", stdin);while (cin >> s){n = s.size();getSA(s, SA, n + 1, 150);getHeight(s, n);init(n);solve();}//freopen_s(&stream, "CON", "r", stdin); //system("pause"); return 0;
}这篇关于后缀数组四·重复旋律4的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






