[Algorithm][滑动窗口][水果成篮][最大连续的一个数 Ⅲ][将x减到0的最小操作数]详细讲解

本文主要是介绍[Algorithm][滑动窗口][水果成篮][最大连续的一个数 Ⅲ][将x减到0的最小操作数]详细讲解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.水果成篮
- 1.题目链接
- 2.算法原理讲解
- 3.代码讲解
2.找到字符串中所有字母异位词
- 1.题目链接
- 2.算法原理讲解
- 3.代码实现
3.串联所有单词的字串
- 1.题目链接
- 2.算法原理讲解
- 3.代码实现
3.最小覆盖字串
- 1.题目链接
- 2.算法原理讲解

1.水果成篮

1.题目链接

水果成篮

2.算法原理讲解

研究的对象是⼀段连续的区间，可以使⽤**「滑动窗⼝」**思想来解决问题
- 将问题转化为：找出一个最长的子数组长度，子数组中不超过两种类型的水果
让滑动窗⼝满⾜：窗⼝内⽔果的种类只有两种
做法：
- 右端⽔果进⼊窗⼝的时候，⽤哈希表统计这个⽔果的频次
- 这个⽔果进来后，判断哈希表的⼤⼩
  - 如果⼤⼩超过2：说明窗⼝内⽔果种类超过了两种
    - 那么就从左侧开始依次将⽔果划出窗⼝，直到哈希表的⼤⼩⼩于等于2，然后更新结果
  - 如果没有超过2：说明当前窗⼝内⽔果的种类不超过两种，直接更新结果ret
优化：
- v1.0中，哈希表有大量的插入删除
- v2.0中，由于水果类型最大值是一个定值，所以可以把hash数组写死，这样以空间换时间，不会存在哈希冲突
  - 此时不用STL容器，无法 $O (1)$ 判断水果种类数量，此时添加一个变量kinds即可

3.代码讲解

// v1.0
// 模型转化为：数组只有两个元素的最大子数组
int TotalFruit(vector<int>& fruits) 
{int ret = 0;unordered_map<int, int> basket; // <水果种类 数量>for(int left = 0, right = 0; right < fruits.size(); right++){basket[fruits[right]]++; // 入窗口while(basket.size() > 2) // 判断{// 出窗口basket[fruits[left]]--;if(basket[fruits[left]] == 0){basket.erase(fruits[left]);}left++;}ret = max(ret, right - left + 1); // 更新数据}return ret;
}
---------------------------------------------------------------
// v2.0 优化
// 改造哈希表，以改善时间复杂度
int TotalFruit(vector<int>& fruits) 
{int ret = 0, kinds = 0;// 水果类型小于一个定值// 以空间换时间int basket[100001] = { 0 };for(int left = 0, right = 0; right < fruits.size(); right++){if(basket[fruits[right]] == 0){kinds++;}basket[fruits[right]]++; // 入窗口while(kinds > 2) // 判断{// 出窗口basket[fruits[left]]--;if(basket[fruits[left]] == 0){kinds--;}left++;}ret = max(ret, right - left + 1); // 更新数据}return ret;
}

2.找到字符串中所有字母异位词

1.题目链接

找到字符串中所有字母异位词

2.算法原理讲解

思路：「滑动窗⼝」 + 「哈希表」
做法：
- 因为字符串p的异位词的⻓度⼀定与字符串p的⻓度相同
  - 所以可以在字符串s中构造⼀个⻓度为与字符串p的⻓度相同的滑动窗⼝，并在滑动中维护窗⼝中每种字⺟的数量
- 当窗⼝中每种字⺟的数量与字符串p中每种字⺟的数量相同时，则说明当前窗⼝为字符串 p的异位词
- 因此可以⽤两个⼤⼩为26的数组来模拟哈希表
  - ⼀个来保存s中的⼦串每个字符出现的个数
  - 另⼀个来保存p中每⼀个字符出现的个数
  - 这样就能判断两个串是否是异位词
    ![[Pasted image 20240326190744.png]]
优化：更新结果的判断条件 -> 利用count来统计窗口中"有效字符"的个数
- 进窗口：进入后 -> if (hashS[in] <= hashP[in]) -> count++
- 出窗口：出去前 -> if (hashS[out] <= hashP[out]) -> count--
- 更新结果：count == len

3.代码实现

// 将问题转化为：p中的字母出现的次数与s中某个字串中出现的次数相同
// v1.0
vector<int> FindAnagrams(string s, string p) 
{vector<int> ret;int hashS[26] = { 0 };int hashP[26] = { 0 };// 将p如hashfor(auto& ch : p){hashP[ch - 'a']++;}// 处理sint len = p.size();for(int left = 0, right = 0; right < s.size(); right++){hashS[s[right] - 'a']++; // 入窗口if(right - left + 1 > len) // 判断窗口是否大了{hashS[s[left++] - 'a']--; // 出窗口}if(right - left + 1 == len) // 尝试更新数据{bool flag = true;for(int i = 0; i < 26; i++){if(hashP[i] != hashS[i]){flag = false;break;}}if(flag){ret.push_back(left);}}}return ret;
}
-----------------------------------------------------------------
// v2.0 优化更新结果的判断条件，不用每次都遍历hash了
vector<int> findAnagrams(string s, string p) 
{vector<int> ret;int hashS[26] = { 0 };int hashP[26] = { 0 };// 将p如hashfor(auto& ch : p){hashP[ch - 'a']++;}// 处理sint count = 0, len = p.size();for(int left = 0, right = 0; right < s.size(); right++){// 入窗口 + 维护countif(++hashS[s[right] - 'a'] <= hashP[s[right] - 'a']){count++; // 入窗口的字符是一个有效字符}if(right - left + 1 > len) // 判断窗口是否大了{// 维护countif(hashS[s[left] - 'a']-- <= hashP[s[left] - 'a']){count--; // 出窗口的元素是一个有效字符}left++; // 出窗口}if(count == len) // 更新结果{ret.push_back(left);}}return ret;
}

3.串联所有单词的字串

1.题目链接

串联所有单词的字串

2.算法原理讲解

如果把每⼀个单词看成⼀个字⺟，问题就变成了找到**「字符串中所有的字⺟异位词」**
- ⽆⾮就是之前处理的对象是⼀个⼀个的字符，这⾥处理的对象是⼀个⼀个的单词
注意的点 && 区别：
- 哈希表：hash<string, int>
- left指针与right指针的移动
  - 移动的步长，是单词的长度len -> 一次跨过一个单词
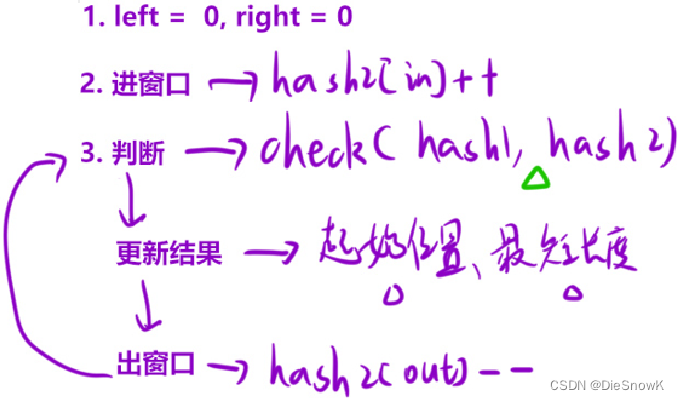
- 滑动窗口执行的次数：len
  - 因为无法确定起点是在哪儿，所以要执行len次
  - 大于len次则没必要，因为第一次与第len+1次是重复的情况…

3.代码实现

vector<int> findSubstring(string s, vector<string>& words) 
{int len = words[0].size();unordered_map<string, int> mapS;unordered_map<string, int> mapV;vector<int> ret;for(auto& str : words){mapV[str]++;}for(int i = 0; i < len; i++) // 滑动窗口的执行次数{int count = 0;for(int left = i, right = i; right + len <= s.size(); right += len){// 入窗口，截取子串，维护countstring str = s.substr(right, len);mapS[str]++;// 看看mapV中是否存在str，以避免插入不需要的值if(mapV.count(str) && mapS[str] <= mapV[str]) {count++;}// 判断窗口是否大了if(((right - left + len) / len) > words.size()){// 维护countstring tmp = s.substr(left, len);if(mapV.count(tmp) && mapS[tmp]-- <= mapV[tmp]){count--;}left += len; // 出窗口}if(count == words.size()) // 更新结果{ret.push_back(left);}}mapS.clear();}return ret;
}

3.最小覆盖字串

1.题目链接

最小覆盖字串

2.算法原理讲解

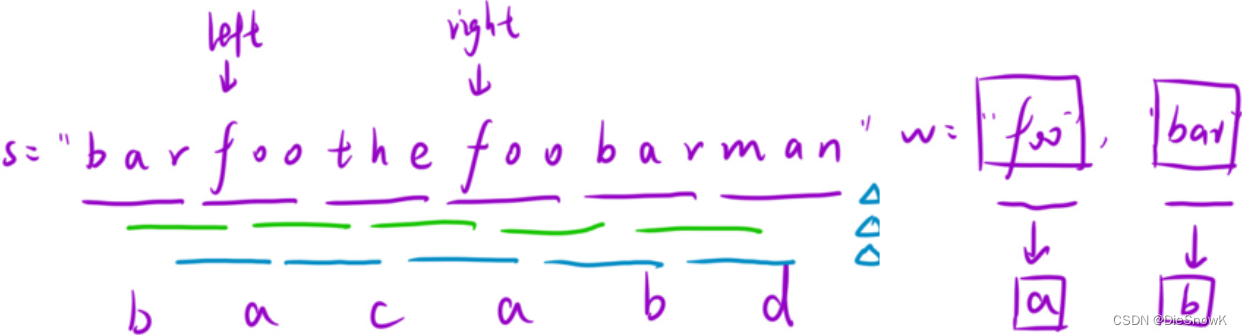
研究对象是连续区间，因此可以尝试使⽤「滑动窗⼝」的思想来解决
如何判断当前窗⼝内的所有字符是符合要求的呢？
- 可以使⽤两个哈希表，其中⼀个将⽬标串的信息统计起来，另⼀个哈希表动态的维护窗⼝内字符串的信息
- 当动态哈希表中包含⽬标串中所有的字符，并且对应的个数都不⼩于⽬标串的哈希表中各个字符的个数，那么当前的窗⼝就是⼀种可⾏的⽅案
优化：判断条件 -> 使用变量count标记有效字符的种类

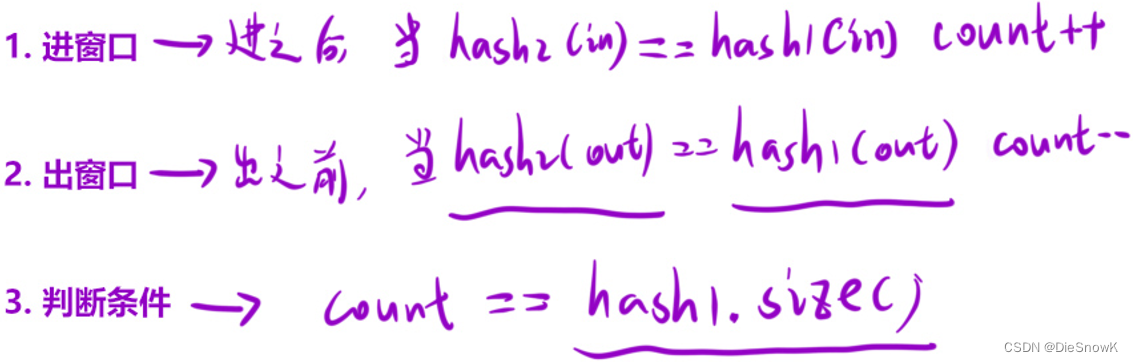
string MinWindow(string s, string t) 
{// 仅用数组可以避免STL的开销，提高效率int hashS[128] = { 0 };int hashT[128] = { 0 };int kinds = 0;for(auto& ch : t){if(hashT[ch]++ == 0){kinds++;}}int begin = -1, minLen = INT_MAX;for(int left = 0, right = 0, count = 0; right < s.size(); right++){// 入窗口char in = s[right];// 维护count，仅统计t中有效字符的种类if(++hashS[in] == hashT[in]){count++;}while(count == kinds) // 判断{   // 更新if(right - left + 1 < minLen){begin = left;    minLen = right - left + 1;}// 出窗口 && 维护countchar out = s[left++];if(hashS[out]-- == hashT[out]){count--;}}}string ret = "";if(begin != -1){ret = s.substr(begin, minLen);    }return ret;
}