【计算机组成原理】运算方法和运算器

本文主要是介绍【计算机组成原理】运算方法和运算器，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 数据格式

在选择计算机的数的表示方式时，需要考虑以下几个因素：
①要表示的数的类型（小数、整数、实数和复数）
②可能的数值范围
③数值精确度
④数据存储和处理所需要的硬件代价

计算机中常用的数据表示格式有两种，一是定点格式，二是浮点格式。

在现代计算机中，通常用补码整数表示整数，用原码小数表示浮点数的尾数部分，用移码表示浮点数的阶码部分

一般来说，
定点格式容许的数值范围有限，要求的处理硬件比较简单。
而浮点格式容许的数值范围很大，要求的处理硬件比较复杂。

1.1 定点数表示方法

定点格式：约定机器中所有数据的小数点位置是固定不变的。由于约定在固定的位置，小数点就不再使用记号“.”来表示。原理上讲，小数点位置固定在哪一位都可以，但是通常将数据表示成纯小数或纯整数。

❗事实上，机器内部并没有小数点，只是人为的约定了小数点的位置。因此，定点数的编码和运算不需要考虑对应的定点数是小数还是整数，只需要关心它们的符号位和数值位即可

1.1.1 定点小数

定点小数是纯小数，约定小数点位置在符号位之后、有效数值部分最高位之前。

1.1.2 定点整数

定点整数是纯整数，约定小数点位置在有效数值部分最低位之后。

---

下面表示的是n+1位的定点数的表示形式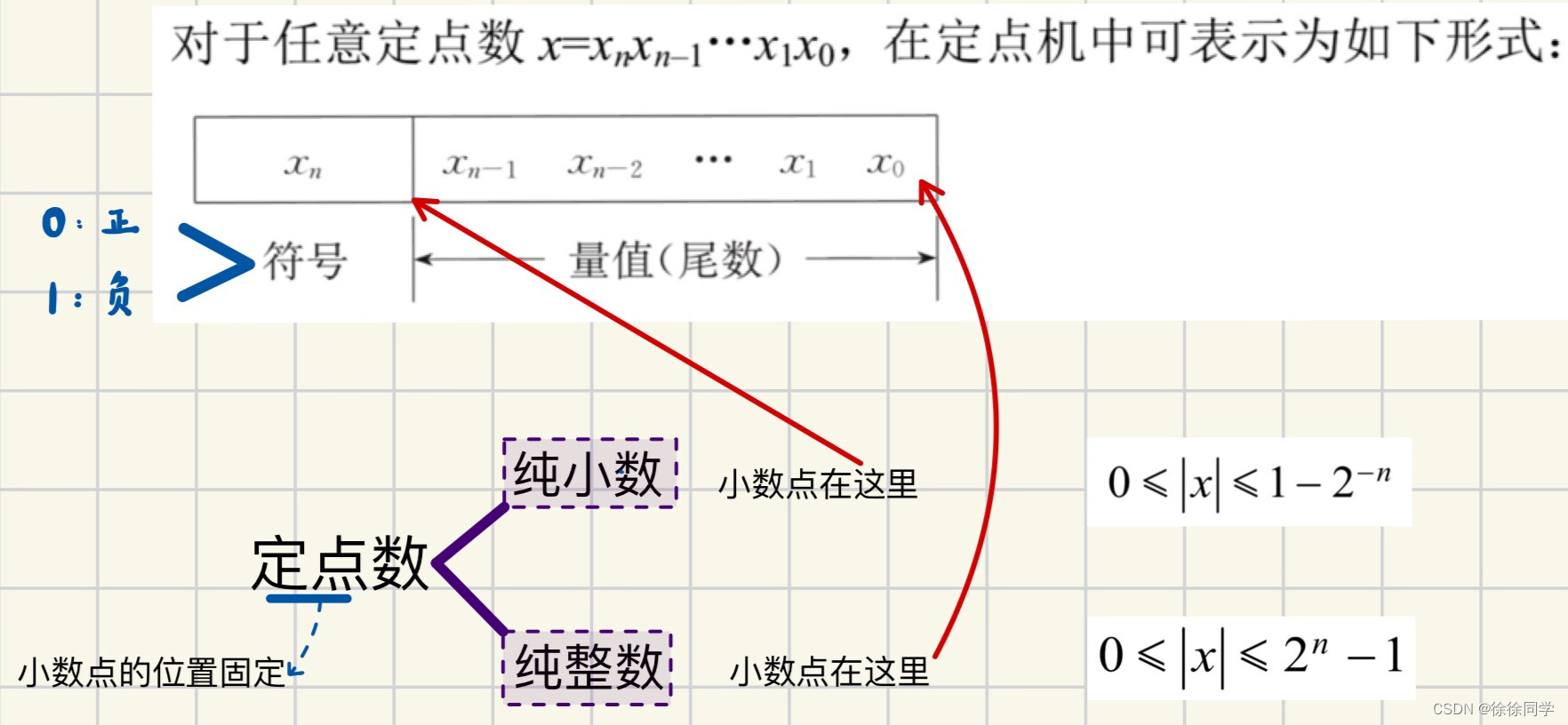
❗注意|x|的取值范围：
如果 x 表示的是纯小数，那么小数点位于 x_n 和 x_n–1 之间。当 x_nx_n–1…x₁x₀ 各位均为 0 时，x的绝对值最小，即 |x|_min = 0 ；当各位均为1时，x的绝对值最大，即 |x|_max = 2^-1 + 2^-2 +…+ 2^-n = 1-2^-n，因此表示范围为：0 ≤ |x| ≤ 1-2^-n

如果 x 表示的是纯整数，那么小数点位于最低位 x₀ 的右边，此时 x 的表示范围为：0 ≤ |x| ≤ 2ⁿ - 1

定点数的运算简称为整数运算

1.2 浮点数表示方法

浮点数表示法是指以适当的形式将比例因子表示在数据中，让小数点的位置根据需要而浮动。这样在位数有限的情况下，既扩大了数的表示范围，又保持了数的精度。

任意一个十进制数 N 可以写成
N = 10^E × M
同样，在计算机中一个任意二进制数 N 可以写成
N = 2^e × M

1.2.1 浮点数表示

通常把浮点数表示为：
N = ( -1 )^S × M × R^E
式中，S取0或1，决定浮点数的符号；
M是一个二进制的定点小数，称为N的尾数，M决定数据的表示精度（因为尾数给出了有效数字的位数）；
E是一个二进制定点整数，称为指数或阶码是一个定点纯整数，决定数据的表示范围（因为阶码指明小数点的位置）。
R是基数，二进制浮点数R=2，十六进制浮点数R=16…

1.2.2 浮点数的规格化

为了让浮点数在运算过程中尽可能多的保留有效数字的位数，使有效数字尽量占满尾数数位，必须在运算过程中对浮点数进行规格化操作

规格化操作：
通过调整一个非规格化的浮点数的尾数和阶码大小，使非零浮点数在尾数的最高数位上保证是一个有效值。

1.2.2.1 尾数为原码表示的规格化

正数为 0.1xx…xx的形式，最大值表示为0.11…1；最小值表示为0.10…0
负数为 1.1xx…xx的形式，最大值表示为1.10…0；最小值表示为1.11…1

1.2.2.2 尾数为补码表示的规格化

符号位和最高数值位一定相反

正数为 0.1xx…xx的形式，最大值表示为0.11…1；最小值表示为0.10…0
负数为 1.0xx…xx的形式，最大值表示为1.01…1；最小值表示为1.00…0

例题1： 若某浮点数表示为 2⁶ × 1.1110100 ，尾数使用补码表示，如何规格化？
❗补码算数左移，低位补0；补码算数右移，高位补1
规格化后：2³ × 1.0100000

详细一点讲，尾数1.1110100 化成原码为：1.0001100，由于小数点左边的1表示符号而不是数值，因此小数点右边高位的3个0可以用阶码来表示。所以对于 1.1110100 ，直接左移三位，低位补0即可。

1.2.3 IEEE754标准⭐

早期的各种计算机系统的浮点数使用不同的机器码表示阶和尾数，给数据交换和比较带来很大的麻烦。→当前的计算机都采用统一的IEEE754标准中的格式来表示浮点数

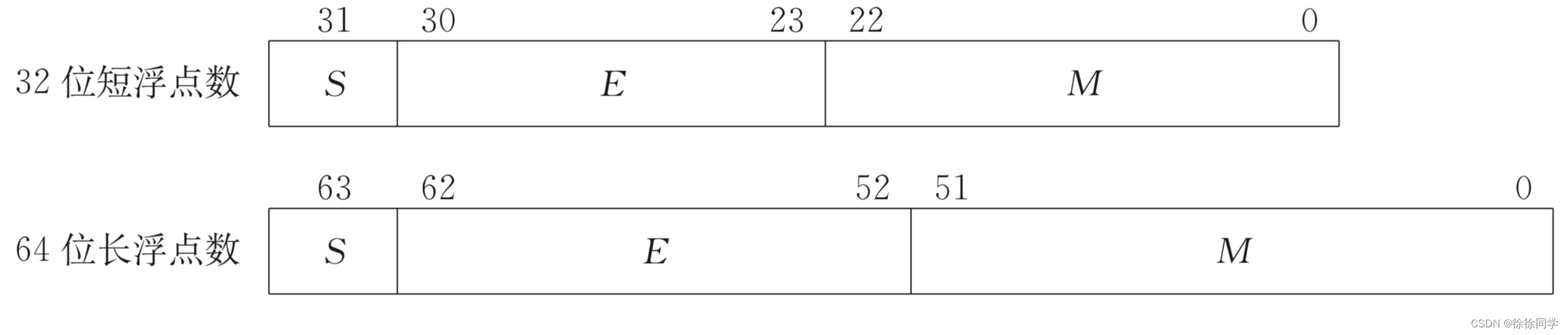
IEEE754标准中，一个规格化的32位浮点数x的真值可表示为：

x = ( -1 )^S × M × 2^e

=( -1 )^S × 1.M × 2^E-127

可能你会问，
①为什么一个是M一个是1.M ？
→❗M位（23bit）：是尾数，小数点在尾数域的最前面，为了尾数的表示精度提高一位，IEEE规格化浮点数规定小数点左边一位必须是1 ，即1.M （比如(1.75)₁₀ = (1.11)_B），这个“ 1 ”通常不予存储，所以M位存储的是有效数据的小数部分，因此尾数域M所表示的值应该是1.M

②为什么一个是e一个是E-127 ？

→❗E位（8bit）：是阶码，IEEE754规定，这个阶码比实际数据中的指数真值多127。如果浮点数指数的真值是e，则阶码 E = e + 127
使用带偏移量的阶码（即后面要说的移码）好处是：将有符号数转化为了无符号数，所以：
· 阶码E不用考虑符号
· 便于两个阶码的比较
· 阶码域大者，指数真值也大

1.3 十进制数串的表示方法

一些计算机能直接处理十进制形式表示的数据，十进制数串在计算机内主要有两种表示形式：

1.3.1 字符串形式

1字节存放一个十进制的数位或符号位。

主存中，这样一个十进制数占用连续多个字节，因此为了指明一个数，需要给出该数在主存的起始地址和串的长度（字节数、位数）。主要用在非数值计算的应用领域。

1.3.2 压缩的十进制数串形式

1字节存放2个十进制的数位。

这种方法比上面那种节省存储空间，也便于直接完成十进制数的算术运算，这种方法采用的较为广泛。跟字符串形式类似，要指明一个数，需要给出该数在主存的起始地址和数字位个数（不含符号位），又称位长

十进制数串表示法的优点是位长可变

用压缩的十进制数串表示一个数

BCD码形式：一个字节放一个十进制的数位或符号位。

压缩BCD码形式：一个字节放两个十进制的数位。

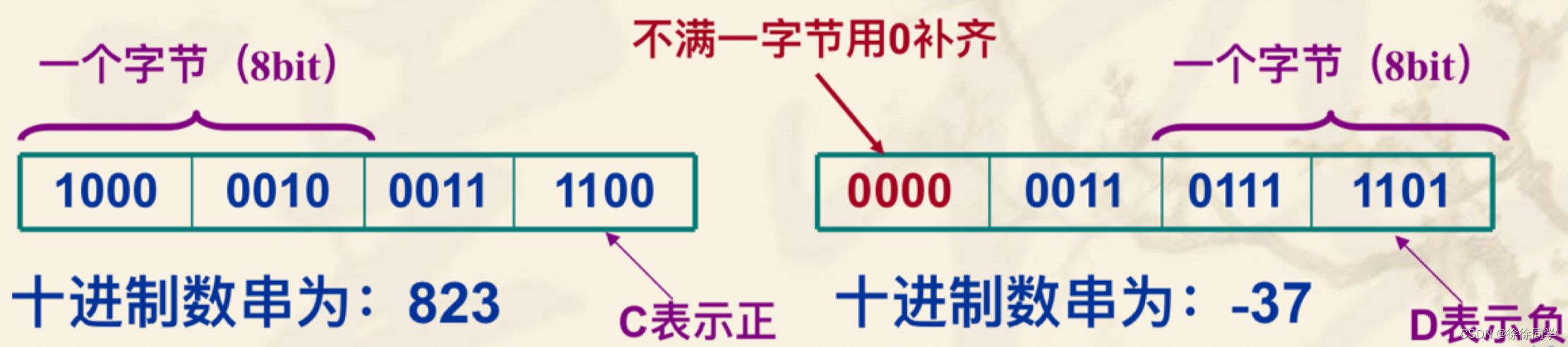
符号位：放在最低数字位之后，占半字节
12（C）表示正号，13（D）表示负号。

规定数位+符号位 之和必须是偶数，当和不为偶数时，应在最高数字位前补一个0

2. 数的机器码表示

前面介绍了数的小数点表示，下面还需要解决数的机器码表示问题。

在计算机中对数据进行运算操作时，符号位如何表示呢?是否也同数值位一道参加运算 操作呢?如参加，会给运算操作带来什么影响呢?

为了妥善地处理好这些问题，就产生了把 符号位和数值位一起编码来表示相应的数的各种表示方法，如原码、补码、反码、移码。 为了区别一般书写表示的数和机器中这些编码表示的数，通常将前者称为真值，后者称为机器码（机器数）

对于同一个数，根据需要，计算机可以使用不同的编码方式进行存储。
原码，反码，补码… 是机器存储一个具体数字的编码方式

机器中数据都是以补码形式出现

2.1 原码表示法

最高位（符号位）表示符号，其余位表示值。
符号位中0表示正数，1表示负数。

0有两种表示法：
[+0]_原 = 0000 0000
[ -0]_原 = 1000 0000

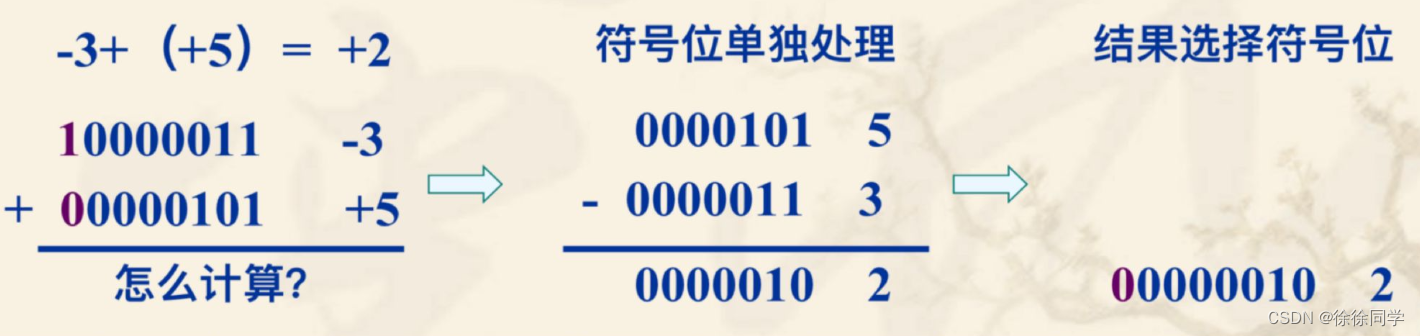
原码表示法简单易懂，但是运算复杂

2.2 反码表示法

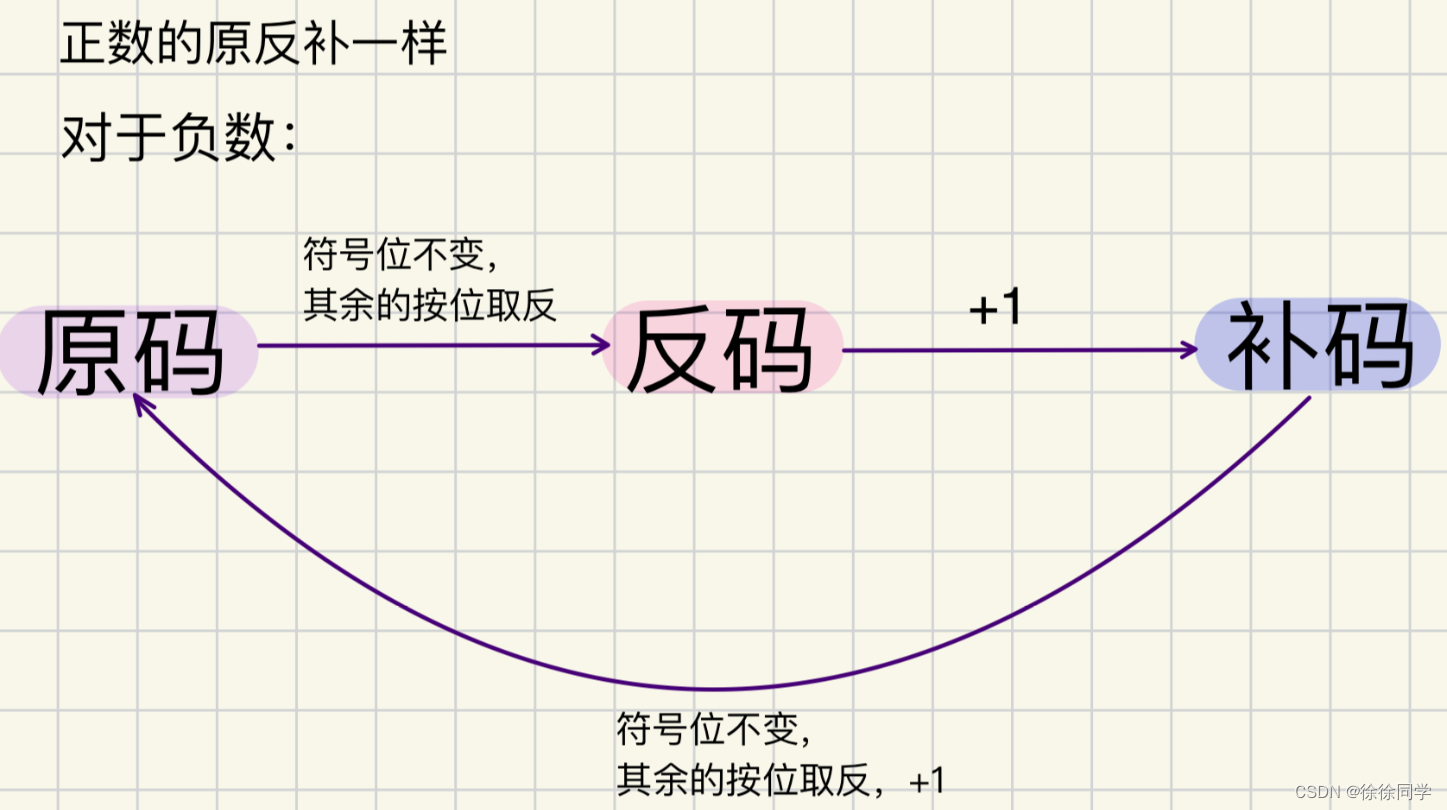
正数的反码 = 原码
负数的反码：符号位不变，其余位取反。

2.3 补码表示法

正数的补码 = 原码
负数的补码：其反码+1

补码的特点：
· 补码的0值唯一
· 补码表示的负数范围可以到2ⁿ （原码反码只能到2ⁿ - 1）
· 补码表示的数据没有符号位（不过我们习惯上认为补码最高位是符号位）

2.4 移码表示法

移码通常用来表示浮点数的阶码，移码只能是整数。

移码就是在真值x上加上一个常数（偏置值），这个常数通常取2ⁿ。相当于x在数轴上向正方向偏移了若干单位，这就是移码为什么叫移码。
[x]_移 = 2ⁿ + x （-2ⁿ ≤ x ≤ 2ⁿ， 机器字长为n+1）

移码的特点：
· 移码的0值唯一
· 一个真值的移码和补码仅相差一个符号位，[x]_补的符号位取反就得到[x]_移
· 移码全0时，对应真值的最小值**-2ⁿ**；移码全1时，对应真值的最大值 2ⁿ - 1
· 移码保持了数据原有大小的顺序，移码大真值大，移码小真值小

这篇关于【计算机组成原理】运算方法和运算器的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---