本文主要是介绍ECIES标准规范对比与实现的思考,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在《椭圆曲线密码学(ECC)基本介绍和总结》中,我们介绍了一些ECC的基本概念,其中包含了基于椭圆曲线进行加解密的混合加密方案ECIES的概念
ECIES并不是某种特定的算法,而是一个基于ECC的加解密框架,从它完整的名字Elliptic Curve Integrated Encryption Scheme就可以看出,“集成的加密框架”。
下图就是这个框架的加密过程和解密过程描述,不难看出,其实对真正的明文数据进行加解密时,并没有用到任何基于ECC的计算,而是使用了对称加解密算法。
在ECIES中,其实是使用ECC的数学原理,对密钥进行保护,基于ECC背后的数学原理,椭圆曲线离散对数问题,保证了解密端所拥有的ECC私钥无法被逆向,从而保护了基于ECC公私钥派生出用于加解密的对称密钥的安全性。
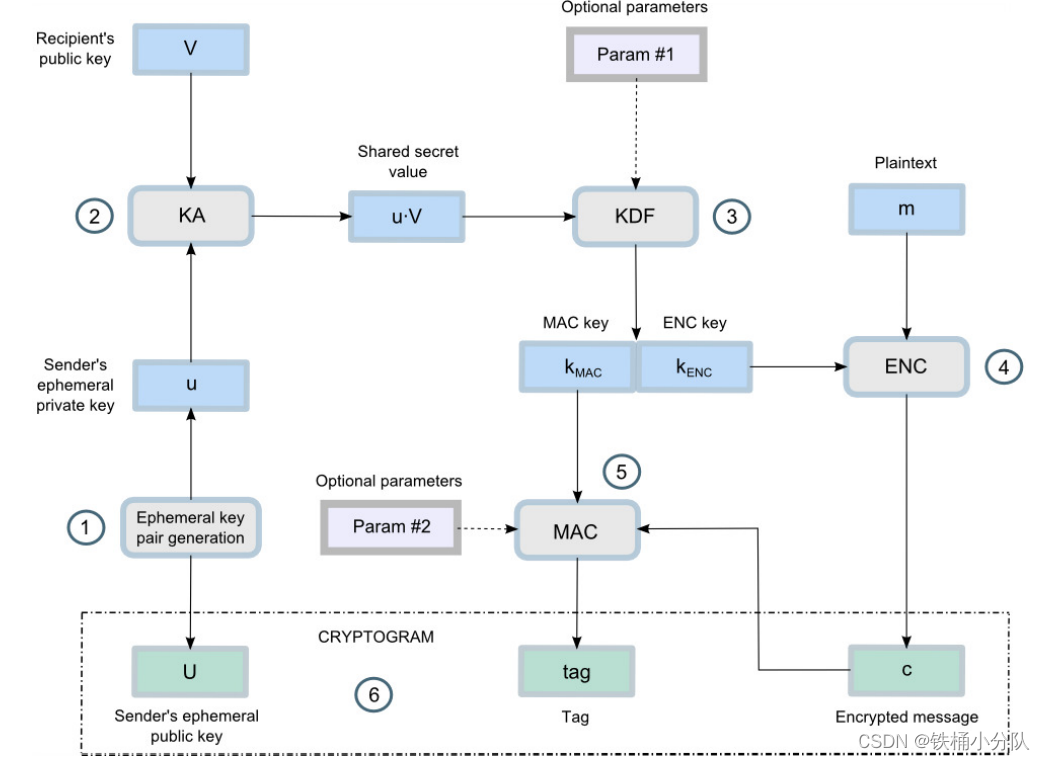
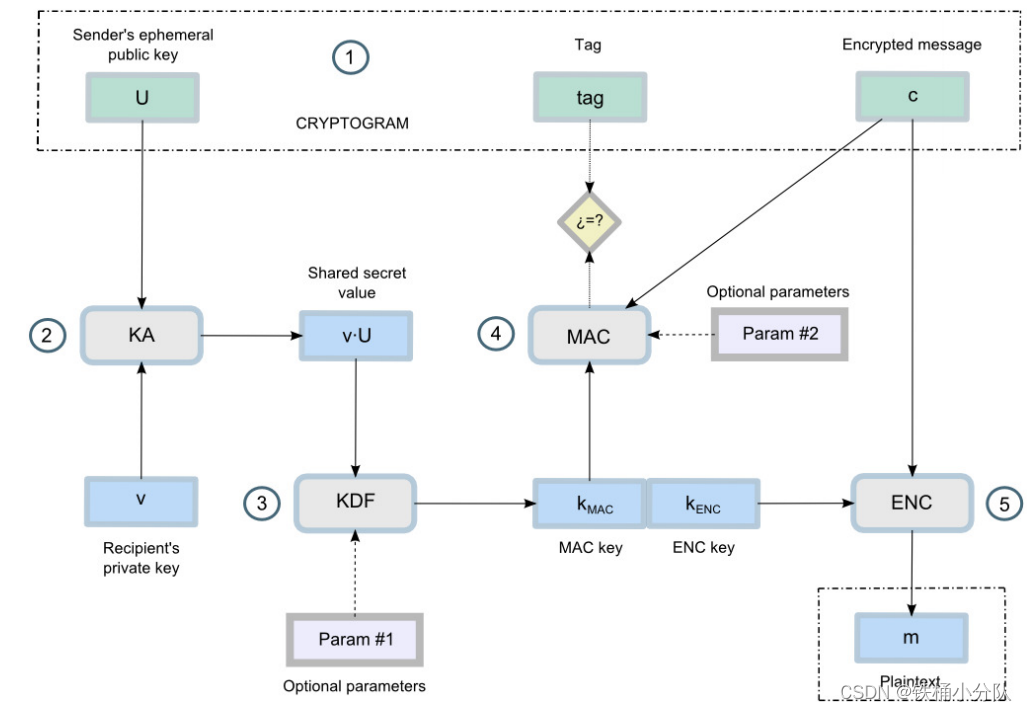
可以看出,所谓的ECIES参数,只不过是具体的密钥派生算法,密钥协商算法,对称加密算法,以及hash算法的类型。因此,一旦涉及到多方的ECIES,就需要各个参与方一起约定ECIES的参数,这样才能有效地实现加解密。从这个角度看,相比于所谓的加解密算法,ECIES倒是更像一个协议,尤其是在用于多方通信时,ECIES就成了一个“应用层协议”。
如前所述,只要是协议或者像协议的事物,通常都会有其技术规范,或者说标准。目前定义ECIES规范的标准主要是:ANSI X9.63, IEEE 1363a, ISO/IEC 18033-2, 和SEC 1。
这四个主流标准中,对于ECIES参数的定义如下:
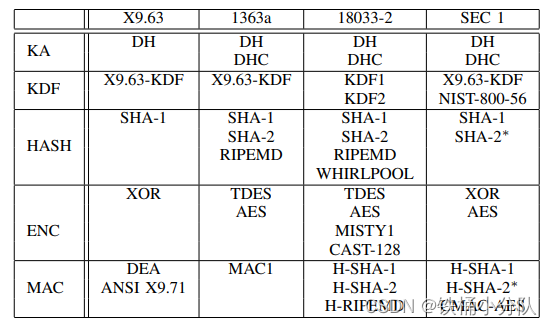
实际上,在上述不同的标准中,即便定义了使用同样的算法,具体的实施细节也会有差异,比如:
同样支持DH作为KA算法,ANSI X9.63只会提取第一个坐标点作为KA算法的输出,而IEEE 1363a则是将得到的完整数据作为KA的输出;同样使用X9.63 KDF作为密钥派生算法,ANSI X9.63选择用KDF计算结果的左半边字节作为ENC Key,右半边数据作为MAC Key。
因此在选择某一标准实现ECIES前,需要有充足的调研,对比开发环境的约束条件(尤其是嵌入式产品,其算力和带宽往往受限,这种情况下采用以压缩方式存储ECC坐标点的标准可能更合适),以及自己能使用的密码库对算法的支持情况(如mbedtls没有直接支持X9.63 KDF)。
目前我国设计的商用密码算法SM2,其实也是一种特定参数下的ECIES,其原理介绍可参考:
https://blog.csdn.net/come_sky/article/details/125952228
直接使用SM2算法,其优势有三
- 现成的ECIES解决方案,避免自己重写ECIES
- 标准化的实现,只需要约定SM2支持的参数即可
- ECC的安全性线源自于使用的曲线,在棱镜门中曝光的信息中,美国计划对SECP256R1曲线植入后门,导致其安全性目前受到质疑,该曲线在基于ECC的应用场景中被大量使用,如果选择曲线,应尽量选择我国自研的商用密码算法中提供的曲线。
这篇关于ECIES标准规范对比与实现的思考的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






