本文主要是介绍B11_NumPy位运算(bitwise_and,bitwise_or,invert,left_shift,right_shift),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
NumPy位运算
NumPy “bitwise_” 开头的函数是位运算函数。
NumPy 位运算包括以下几个函数:
| 函数 | 描述 |
|---|---|
| bitwise_and | 对数组元素执行位与操作 |
| bitwise_or | 对数组元素执行位或操作 |
| invert | 按位取反 |
| left_shift | 向左移动二进制表示的位 |
| right_shift | 向右移动二进制表示的位 |
| 注:也可以使用"&"、"~"、" | “和”^"等操作符进行计算。 |
bitwise_and
bitwise_and() 函数对数组中整数的二进制形式执行位与运算。
实例:
import numpy as npprint('13和17的二进制形式:')
a,b = 13,17
print(bin(a),bin(b))
print('\n')print('13和17的位与:')
print(np.bitwise_and(13,17))
输出结果为:
import numpy as npprint('13和17的二进制形式:')
a,b = 13,17
print(bin(a),bin(b))
print('\n')print('13和17的位与:')
print(np.bitwise_and(13,17))
输出结果为:
13和17的二进制形式:
0b1101 0b10001
13和17的位与:
1
以上实例可以用下表来说明:

bitwise_or
bitwise_or()函数对数组中整数的二进制形式执行位或运算。
import numpy as npa,b = 13,17
print('13和17的二进制形式:')
print(bin(a),bin(b))
print('\n')print('13和17的位或:')
print(np.bitwise_or(13,17))
输出结果为:
13和17的二进制形式:
0b1101 0b10001
13和17的位或:
29
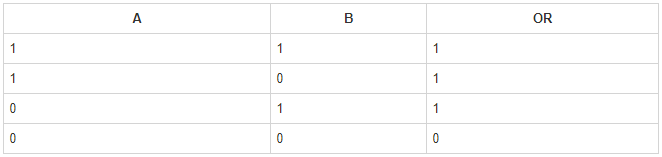
以上实例可以用下表来说明:

位或操作运算规律如下:
invert
invert() 函数对数组中整数进行位取反运算,即 0 变成 1,1 变成 0。
对于有符号整数,取该二进制数的补码,然后 +1。二进制数,最高位为0表示正数,最高位为 1 表示负数。
看看 ~1 的计算步骤:
- 将1(这里叫:原码)转二进制= 00000001
- 按位取反 = 11111110
- 发现符号位(即最高位)为1(表示负数),将除符号位之外的其他数字取反 = 10000001
- 末位加1取其补码 = 10000010
- 转换回十进制=-2

实例
import numpy as npprint('13 的位反转,其中 ndarray 的 dtype 是 uint8:')
print(np.invert(np.array([13], dtype=np.uint8)))
print('\n')
# 比较 13 和 242 的二进制表示,我们发现了位的反转print('13 的二进制表示:')
print(np.binary_repr(13, width=8))
print('\n')print('242 的二进制表示:')
print(np.binary_repr(242, width=8))
输出结果为:
13 的位反转,其中 ndarray 的 dtype 是 uint8:
[242]
13 的二进制表示:
00001101
242 的二进制表示:
11110010
left_shift
left_shift() 函数将数组元素的二进制形式向左移动到指定位置,右侧附加相等数量的 0。
import numpy as npprint('将 10 左移两位:')
print(np.left_shift(10, 2))
print('\n')print('10 的二进制表示:')
print(np.binary_repr(10, width=8))
print('\n')print('40 的二进制表示:')
print(np.binary_repr(40, width=8))
# '00001010' 中的两位移动到了左边,并在右边添加了两个 0。
输出结果为:
将 10 左移两位:
40
10 的二进制表示:
00001010
40 的二进制表示:
00101000
right_shift
right_shift() 函数将
数组元素的二进制形式向右移动到指定位置,左侧附加相等数量的 0。
import numpy as npprint('将 40 右移两位:')
print(np.right_shift(40, 2))
print('\n')print('40 的二进制表示:')
print(np.binary_repr(40, width=8))
print('\n')print('10 的二进制表示:')
print(np.binary_repr(10, width=8))
# '00001010' 中的两位移动到了右边,并在左边添加了两个 0。
输出结果为:
将 40 右移两位:
10
40 的二进制表示:
00101000
10 的二进制表示:
00001010
这篇关于B11_NumPy位运算(bitwise_and,bitwise_or,invert,left_shift,right_shift)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





