本文主要是介绍arcgis中坡向计算工作原理说明,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
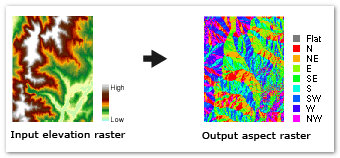
用于识别出从每个像元到其相邻像元方向上值的变化率最大的下坡方向。坡向可以被视为坡度方向。输出栅格中各像元的值可指示出各像元位置处表面的朝向的罗盘方向。将按照顺时针方向进行测量,角度范围介于 0(正北)到 360(仍是正北)之间,即完整的圆。不具有下坡方向的平坦区域将赋值为 -1。
坡向数据集中每个像元的值都可指示出该像元的坡度朝向。

从概念上讲,坡向工具将根据要处理的像元或中心像元周围一个 3 x 3 的像元邻域的 z 值拟合出一个平面。该平面的朝向就是要处理的像元的坡向。
下图显示的是输入高程数据集和输出坡向栅格。
1. 坡向算法
移动的 3 x 3 窗口会访问输入栅格中的每个像元,而每次位于窗口中心的像元的坡向值将通过一种将纳入八个相邻像元值的算法进行计算。这些像元使用字母 a 至 i 进行标识,其中 e 表示当前正在计算坡向的像元。
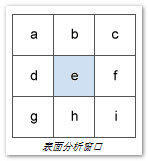
像元 e 在 x 方向上的变化率将通过以下算法进行计算:
[dz/dx] = ((c + 2f + i) - (a + 2d + g)) / 8像元 e 在 y 方向上的变化率将通过以下算法进行计算:
[dz/dy] = ((g + 2h + i) - (a + 2b + c)) / 8代入像元 e 在 x 方向和 y 方向上的变化率,坡向将通过以下算法进行计算:
aspect = 57.29578 * atan2 ([dz/dy], -[dz/dx])然后,坡向值将根据以下规则转换为罗盘方向值(0 到 360 度):
2. 坡向计算示例
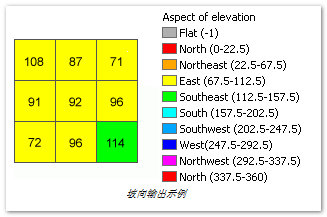
示例中,将计算移动窗口内中心像元的坡向值。

中心像元 e 在 x 方向上的变化率为:
[dz/dx] =((c + 2f + i)-(a + 2d + g))/8=((85 + 170 + 84))-(101 + 202 + 101))/8=-8.125
像元 e 在 y 方向上的变化率为:
[dz/dy] = ((g + 2h + i)-(a + 2b + c) / 8 =((101 + 182 + 84)-(101 + 184 + 85))/ 8 = -0.375
坡向计算如下:
aspect = 57.29578 * atan2 ([dz/dy], -[dz/dx])= 57.29578 * atan2 (-0.375, 8.125) = -2.64
由于计算得出的值小于零,则根据最终规则得出:
cell = 90.0 - aspect = 90 - (-2.64)= 90 + 2.64 = 92.64
中心像元 e 的值 92.64 表明它的坡向为朝东。
3. 参考文献
Burrough, P. A., and McDonell, R. A., 1998. Principles of Geographical Information Systems (Oxford University Press, New York), 190 pp.
这篇关于arcgis中坡向计算工作原理说明的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




