找到冠军 II(Lc2924)——统计入度

本文主要是介绍找到冠军 II(Lc2924)——统计入度，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一场比赛中共有 n 支队伍，按从 0 到  n - 1 编号。每支队伍也是 有向无环图（DAG） 上的一个节点。

给你一个整数 n 和一个下标从 0 开始、长度为 m 的二维整数数组 edges 表示这个有向无环图，其中 edges[i] = [ui, vi] 表示图中存在一条从 ui 队到 vi 队的有向边。

从 a 队到 b 队的有向边意味着 a 队比 b 队 强 ，也就是 b 队比 a 队 弱 。

在这场比赛中，如果不存在某支强于 a 队的队伍，则认为 a 队将会是 冠军 。

如果这场比赛存在 唯一 一个冠军，则返回将会成为冠军的队伍。否则，返回 -1 。

注意

• 环 是形如 a1, a2, ..., an, an+1 的一个序列，且满足：节点 a1 与节点 an+1 是同一个节点；节点 a1, a2, ..., an 互不相同；对于范围 [1, n] 中的每个 i ，均存在一条从节点 ai 到节点 ai+1 的有向边。
• 有向无环图 是不存在任何环的有向图。

示例 1：

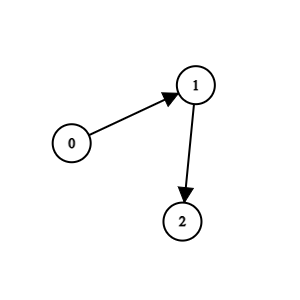
输入：n = 3, edges = [[0,1],[1,2]]
输出：0
解释：1 队比 0 队弱。2 队比 1 队弱。所以冠军是 0 队。

示例 2：

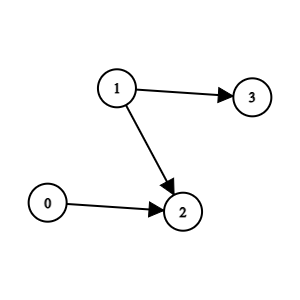
输入：n = 4, edges = [[0,2],[1,3],[1,2]]
输出：-1
解释：2 队比 0 队和 1 队弱。3 队比 1 队弱。但是 1 队和 0 队之间不存在强弱对比。所以答案是 -1 。

提示：

• 1 <= n <= 100
• m == edges.length
• 0 <= m <= n * (n - 1) / 2
• edges[i].length == 2
• 0 <= edge[i][j] <= n - 1
• edges[i][0] != edges[i][1]
• 生成的输入满足：如果 a 队比 b 队强，就不存在 b 队比 a 队强
• 生成的输入满足：如果 a 队比 b 队强，b 队比 c 队强，那么 a 队比 c 队强

问题简要描述：返回冠军的队伍

Java 

class Solution {public int findChampion(int n, int[][] edges) {int[] indeg = new int[n];for (int[] e : edges) {indeg[e[1]]++;}int ans = -1, cnt = 0;for (int i = 0; i < n; i++) {if (indeg[i] == 0) {cnt++;ans = i;}}return cnt == 1 ? ans : -1;}
}

 Python3

class Solution:def findChampion(self, n: int, edges: List[List[int]]) -> int:indeg = [0] * nfor _, v in edges:indeg[v] += 1return -1 if indeg.count(0) != 1 else indeg.index(0)        

TypeScript

function findChampion(n: number, edges: number[][]): number {let indeg: number[] = Array(n).fill(0);for (const [u, v] of edges) {indeg[v]++;}let [ans, cnt] = [-1, 0];for (let i = 0; i < n; i++) {if (indeg[i] == 0) {cnt++;ans = i;}}return cnt == 1 ? ans : -1;
};

 

这篇关于找到冠军 II(Lc2924)——统计入度的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---