本文主要是介绍或颠覆美国十年PQC布局,中国学者「破解格密码」!,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
4月10日,清华大学交叉信息研究院的陈一镭助理教授在eprint平台上发表了一篇划时代的论文,提出了一种全新的量子算法,可以破解格密码。
论文链接:
https://eprint.iacr.org/2024/555
清华大学在官方公告中表示:“这项工作仍在同行评议中。如果被验证为正确,这一突破不仅会将量子计算推进到了一个新的时代,还将对密码学、安全等领域产生深远的影响。”

公告链接:
https://mp.weixin.qq.com/s/IdSmmJI2npQeRORRHHAScQ
图灵奖得主、量子计算领域权威、清华交叉信息研究院院长姚期智对此给出了高度评价:“作为一个青年教师,陈一镭能勇于挑战如格密码这样的世界级科学难题,令人赞佩!”
目前,这项研究成果还未经过同行验证。一旦通过,它在科学上的意义将是双层的: 第一,这将是自30年前Peter Shor提出大数分解的量子算法以来,最重要的量子算法突破。第二,这将对美国NIST过去10年来选择后量子密码设计的思路产生颠覆性的影响,因为多数选出的后量子密码方案都是基于格上的近似最短向量问题(Approximate Shortest Vector Problems in Lattices,简称Lattice Problems)或带错误学习问题(Learning with Errors,LWE)。总之,陈一镭的工作无疑将使他们的安全性受到质疑。
这篇论文提出的算法及分析极为新颖而深奥。回想Wiles 1994年解决费马大定理(Fermat's Last Theorem),以及Perelman 2002年解决庞佳莱猜想(Poincaré Conjecture)后,都经过一年以上专家们方能彻底认证其正确性。
陈一镭的工作,预料也需要数月时间才能完成验证认可,我们静候科学界对此工作的后续反应。

目前,RSA(Rivest-Shamir-Adleman)算法是最为广泛采用的一种非对称加密技术,它允许信息发送者使用公开密钥进行信息加密,而只有持有相应私钥的接收者才能解密信息。这样的设计确保了即便信息在传输过程中被截获,也无法被未授权的第三方解密。密钥的安全性主要依赖于其长度,即所用密钥的位数。
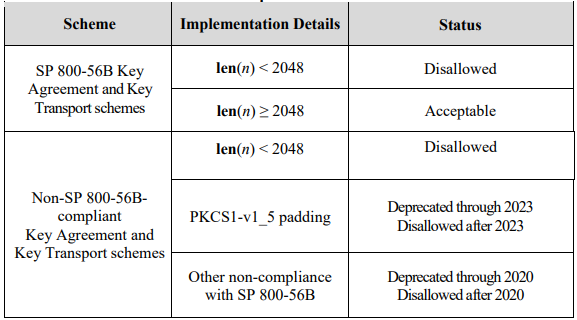
基于RSA的密钥协议和密钥传送计划的批准状态。目前,美国国家标准与技术研究院(NIST)推荐的RSA密钥长度为2048位
RSA算法依赖于一个基于两个大素数乘积的复杂数学公式,该乘积构成了生成安全密钥的基础。RSA的安全性核心在于因式分解的计算难度,即确定两个原始质数的难度。对于足够大的数,即便是基础乘法运算也无法轻易实现其因式分解。
然而,这一切在1994年发生了变化,麻省理工学院的数学家Peter Shor提出了一种算法,解决了离散对数问题,从而为攻破RSA加密铺平了道路。离散对数问题本质上是一种计算简单但难以逆向的函数,如因式分解。在量子计算机上应用Shor算法,寻找RSA的因子由此可能变得可行。
瑞士苏黎世IBM研究院的安全研究小组经理Michael Osborne指出:“量子计算机擅长处理的问题类型非常有限。它们并不适合解决所谓的精确问题,因为它们的运行基于概率性。不幸的是,由于Shor算法本质上适合量子计算机处理问题的不同方式,因此得以从量子加速中受益。”
椭圆曲线加密(ECC)是另一种流行的非对称加密技术,基于椭圆曲线数学。ECC在速度和复杂性上都优于RSA,并构成了区块链安全的基础。然而,量子计算机的速度潜力同样可能威胁到ECC的安全性,因为它们的数学基础与Diffie-Hellman密钥交换相似。
另一方面,对称加密使用单一密钥进行加密和解密,其中最著名的例子是美国国家安全局批准的AES。基于哈希值的这些加密方法相对不易受到Shor算法的影响,但可能面临其他类型的攻击。
NIST的后量子密码学项目负责人、数学家Dustin Moody解释道:“总体而言,Shor算法几乎可以破解我们目前使用的所有公钥密码体系,包括RSA、Diffie-Hellman及其椭圆曲线版本。对于AES这样的对称算法以及SHA2和SHA3等哈希函数,我们不必更换算法,因为它们尚未被破解。在最坏的情况下,我们只需要使用稍长的密钥即可。”
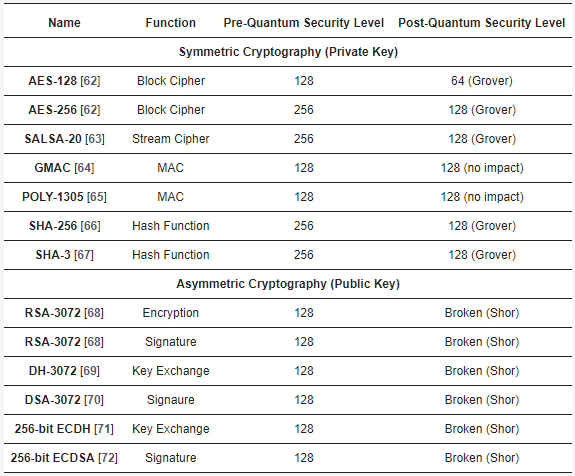
广泛部署的经典密码系统及其针对已知最佳前量子和后量子攻击的安全级别摘要
去年,纽约大学教授Oded Regev的研究可能进一步加快了Shor算法的执行速度,引发了对现有加密方法安全性的进一步关注。

至今,RSA加密技术的挑战赛一直在搜寻最佳的安全措施,但发现许多看似有希望的解决方案实际上仍存在漏洞。
Flex Logix的副总裁Jayson Bethurem表示:“NIST最初收到了69项竞赛提案,经过5年的筛选,如今只剩下4个备选方案。最终的选定结果预期将在今年夏季公布。目前,仍有一些基于哈希的算法持续进展。在这场持久战中幸存下来的,往往是那些通过增加密钥长度来提高安全性的算法:这意味着数据路径变宽,相应地,因为数据路径的潜力巨大,所需时间来破解这些组合也会大大增加。”
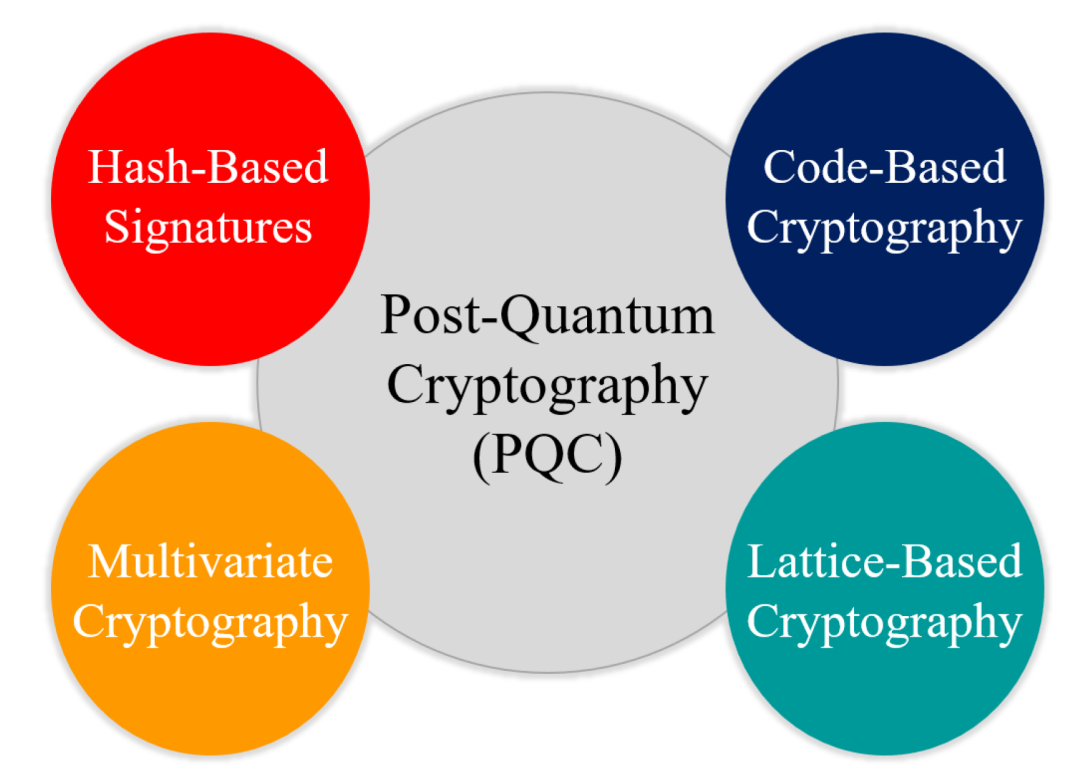
后量子密码学(PQC)的基本类型
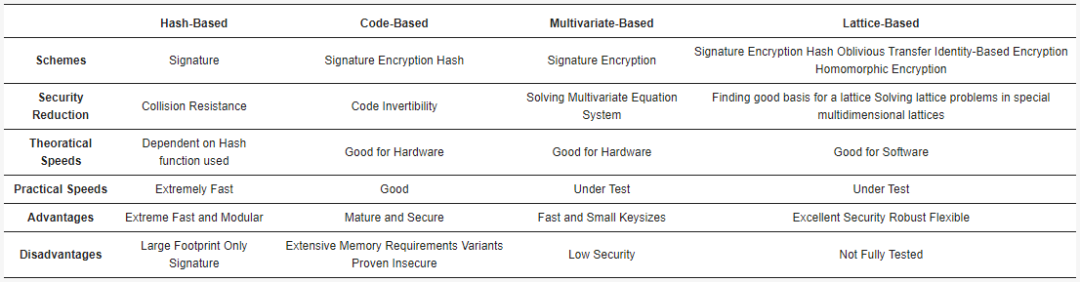
后量子密码学不同技术之间的比较
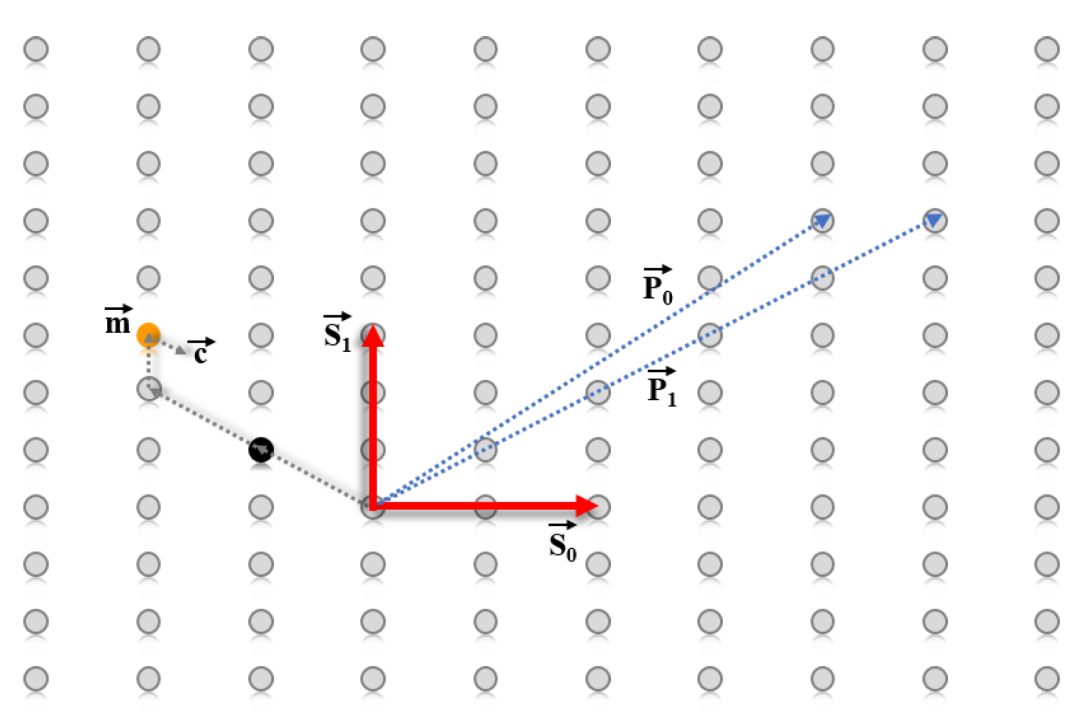
二维结构中基于格的加密(LBC)示例:秘密“对称基”(symmetrical base)为[𝑆0→,𝑆1→];公开“非对称基”(asymmetrical base)为[P0→,P1→]。发送方利用[P0→,P1→]将信息勾勒到格点m,并添加误差向量,得到结果点[𝐶→]。与其他格点相比,[𝐶→]点与[m→]点相邻。因此,接收者可以利用完善的“秘密基”(secret-base)[𝑆0→,𝑆1→],轻松检索[m→](点向量);而对于只拥有“扰乱基”(scrambled base)[P0→,P1→]的攻击者来说,这是一项艰巨的计算。对于量子安全方案来说,格的n维数必须远远大于2,就像这个例子一样
格密码系统使用称为“格”(lattice)的几何结构构建,并使用称为矩阵的数学阵列表示
似乎,既能有效抵抗已知的攻击方式,又能实际应用的加密方法,落在了基于格的算法上。
目前流行的基于格的算法是对旧技术的标准化。Rambu公Best司的贝斯特说:“有一种更新的密钥交换机制,称为CRYSTALS-Kyber算法,还有一种更新的数字签名算法,称为CRYSTALS-Dilithium算法。”
NIST的Moody也表示:“虽然基于晶格的加密技术无疑是最有前途的,但我们还是选择了四种算法进行标准化。”——不过,其中三种基于格。

格密码学的安全性根植于格问题的计算复杂性,比如寻找最短向量问题(SVP)和最近向量问题(CVP)。这些问题即便面对量子计算机的挑战,也被认为是难以直接解决的。与依赖于传统数学难题的加密技术相比,格密码学因其对量子攻击的天生抵抗力而成为后量子密码学的强有力候选。
格中的近似最短向量问题(Approximate Shortest Vector Problems in Lattices,简称Lattice Problems)及其等价问题——带错误的学习问题(Learning with Errors,简称LWE),长久以来被视为算法领域的难题,超出了传统计算能力的解决范畴。
2005年,Oded Regev引入的LWE问题,挑战的是在加入随机噪声后,如何从一组线性方程恢复未知的密钥向量。这一问题之所以关键,不仅因为它建立在坚实的理论基础之上,更因为它能被应用于开发各式加密协议,如全同态加密、安全多方计算和零知识证明等。LWE问题的复杂性确保了,即使攻击者获取了部分信息,也无法有效解码,从而为信息传输和存储提供了坚固的安全屏障。

论文链接:
https://cims.nyu.edu/~regev/papers/lwesurvey.pdf
因此,攻破LWE问题不仅是推动量子计算和密码学理论发展的关键,也是确保数字世界在量子时代保持安全的重要步骤。
那么,量子计算机有望能破解Lattice Problems以及LWE吗?这个问题一直是研究的热点,但直到现在都缺乏实质性的进展。
如今,陈一镭助理教授的研究成果,提出了一种全新的量子算法,专门解决LWE及其等价的格问题,引领了这一研究领域向前迈出了重要的一步。

陈一镭提出的量子算法基于两项技术创新:具有复杂方差的高斯函数(Gaussian functions with complex variances)和窗口化的量子傅里叶变换。这两种方法的结合不仅解决了LWE问题,而且为量子计算领域提供了新的数学工具和算法框架。
在陈一镭的算法中,具有复杂方差的高斯函数起到了核心作用。传统的高斯函数在量子算法中已经有广泛应用,而具有复杂方差的高斯函数是基于复数域上的高斯分布,这使得算法能够有效地“编码”和处理带有噪声的信息。在LWE问题中,噪声的存在是解决问题的主要难点之一,通过使用具有复杂方差的高斯函数,算法能够在量子态上精确地控制和利用这些噪声,从而有效地逼近并最终解决问题。
量子傅里叶变换(QFT)是量子计算中的一项基础操作,用于将量子信息从时域转换到频域。陈一镭引入的窗口化量子傅里叶变换,则是对QFT的一个创新性扩展,通过在变换前后引入“窗口”函数,进一步优化了信息的处理效率和精度。这种方法使得算法能够在保持傅里叶变换优势的同时,通过窗口函数对信息进行预处理和后处理,有效地抑制了噪声,提高了算法的稳定性和准确度。
文中,作者运行了一个由9大步骤组成的量子子程序,时间复杂度为O(n)次。每次运行量子子程序时都会获得一个经典线性方程,其中随机系数在
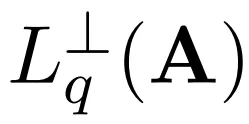
中的最短向量上(与LWE秘密和误差向量相关)。因此,运行O(n)次后将得到一个满秩线性方程组,并通过高斯消元法计算LWE秘密项和误差项。


这些技术创新的结合,为解决LWE问题提供了一种全新的途径。通过复方差的高斯函数,算法能够在量子层面上精确地处理和利用问题中的噪声信息,而窗口化的量子傅里叶变换则进一步增强了算法处理信息的能力,使其能够在多项式时间内高效地找到LWE问题的解。
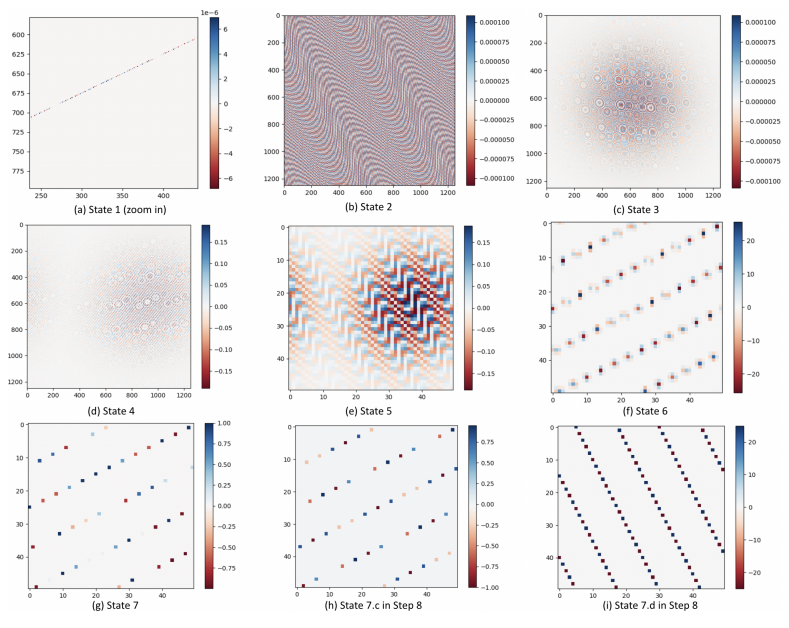
步骤1 - 8中获得的量子态的概念验证演示。所有图片描述的都是状态振幅的实部(real part)
这不仅克服了以往在解决LWE问题上的效率和准确性难题,也为后量子密码学的发展提供了新的理论基础和技术路径。


并且,从论文的致谢部分可以看出,纽约大学的计算机科学家Oded Regev——一位在理论计算机科学领域推动格密码学和容错学习问题研究的先驱,可能已经审阅了这篇论文的手稿。
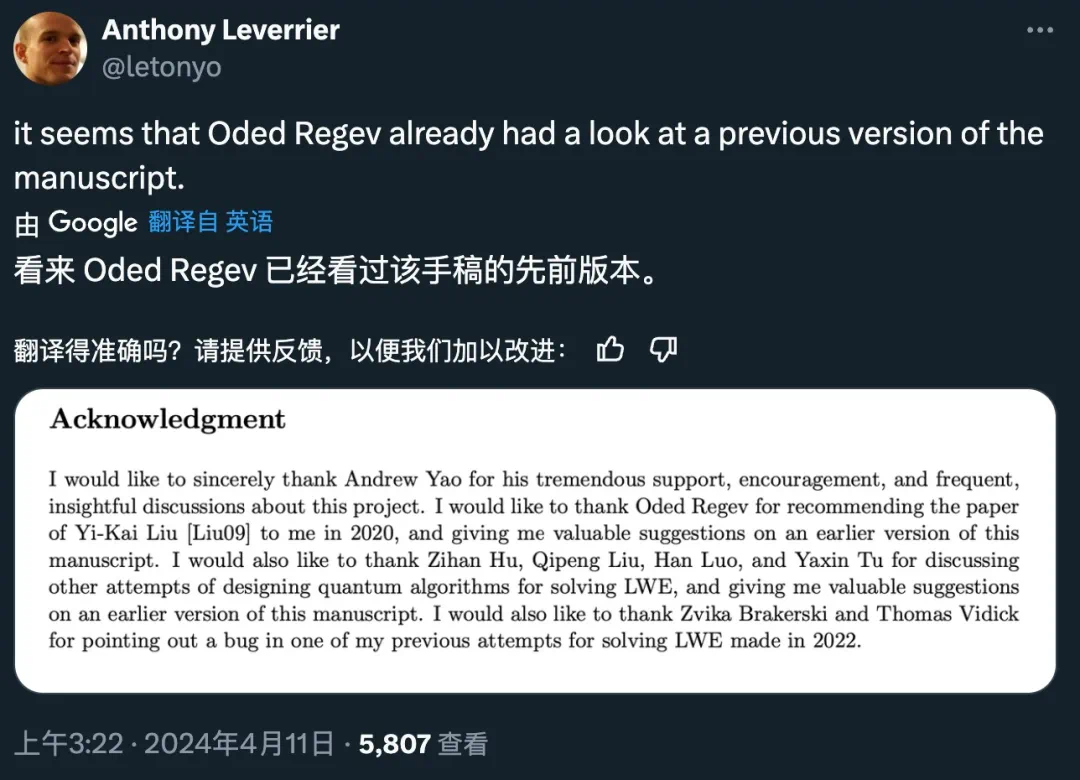
这项研究成果如果能够顺利通过同行评审,预计将促使对当前及未来加密技术安全性的全面重新评估——特别是对于美国国家标准与技术研究院(NIST)正在进行的后量子密码学标准化过程。
LWE问题的解决难度是格密码学及其加密应用安全性的核心。倘若该问题被量子算法有效攻破,则基于LWE的加密方案——包括若干NIST后量子密码学标准候选方案,可能面临安全风险。这不仅迫使加密界重新审视现有加密技术的安全强度,亦有可能催生对新的、更为强大加密技术的研究与开发的加速。
尽管陈一镭的算法尚未被证实挑战到这些候选方案的安全性,但其研究为量子计算的攻击潜力提供了一个具体案例,凸显了持续对这些算法进行研究与改进的重要性,以确保它们在未来量子时代的安全可靠。
这一里程碑式的工作不仅证明了理论计算机科学的不断进步,也提醒我们在量子时代,现有的密码学基石可能需要重新评估和加固。陈一镭的工作,如同之前的科学巨匠们解开长久以来科学界悬而未决的问题一样,有望为整个科学社区和未来的技术应用指明方向。
参考链接(上下滑动查看更多):
[1]https://mp.weixin.qq.com/s/IdSmmJI2npQeRORRHHAScQ
[2]https://en.wikipedia.org/wiki/RSA_(cryptosystem)
[3]https://nvlpubs.nist.gov/nistpubs/SpecialPublications/NIST.SP.800-131Ar2.pdf
[4]https://csrc.nist.gov/projects/post-quantum-cryptography
[5]https://www.mdpi.com/2624-831X/2/1/5
[6]https://semiengineering.com/quantum-computing-challenged-by-security-error-correction/
[7]https://www.jiqizhixin.com/articles/2024-04-11-6
[8]https://mp.weixin.qq.com/s/kHG2E0It9JPAYGYfWwW8VA
这篇关于或颠覆美国十年PQC布局,中国学者「破解格密码」!的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


