本文主要是介绍2023ICPC网络预选赛 ( 2 ) (2) C.Covering【2-SAT、前后缀虚拟节点区间连边】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
C.Covering

题意
给定一个长度为 n n n 的正整数数组 a a a,现在要从中选择一些下标,满足:
- 对于每个下标 i i i, i i i 和 i − 1 i - 1 i−1 至少 有一个被选
- 对于所有选择的下标,任意两个下标 i , j ( i ≠ j ) , a [ i ] ≠ a [ j ] 或 a [ i + 1 ] ≠ a [ j + 1 ] i,j(i \neq j),\hspace{4pt} a[i] \neq a[j] 或 a[i + 1] \neq a[j+1] i,j(i=j),a[i]=a[j]或a[i+1]=a[j+1]
- 不能选择下标 n n n
分析可以发现:下标 1 1 1 一定要被选,因为它前面没有下标了,下标 n − 1 n - 1 n−1 一定要被选,因为下标 n n n 不能选
考虑 2 − S A T 2-SAT 2−SAT:
- 对于限制 1 1 1:连边 i ˉ → i − 1 \bar i \rarr i - 1 iˉ→i−1, i ˉ → i + 1 \bar i \rarr i + 1 iˉ→i+1
- 对于限制 2 2 2:连边 i → 集合 S i \rarr 集合 S i→集合S,集合 S = ( j , ∀ j ≠ i , a [ j ] = a [ i ] ∧ a [ j + 1 ] = a [ i + 1 ] ) S = (j, \forall j \neq i, \hspace{3pt} a[j] = a[i] \wedge a[j + 1] = a[i + 1]) S=(j,∀j=i,a[j]=a[i]∧a[j+1]=a[i+1])
- 由于 1 1 1 必选, n n n 必不选,因此可以连边: 1 ˉ → 1 \bar 1 \rarr 1 1ˉ→1, n → n ˉ n \rarr \bar n n→nˉ,用以确定是否存在可行解
如果对于限制 2 2 2 暴力连边,复杂度太高,考虑优化:
可以发现对于每种键值 ( a [ i ] , a [ i + 1 ] ) (a[i], a[i + 1]) (a[i],a[i+1]),它们要连的集合都是除了自己本身以外的拥有相同键值的所有点,这里会分割成一个前缀和后缀:
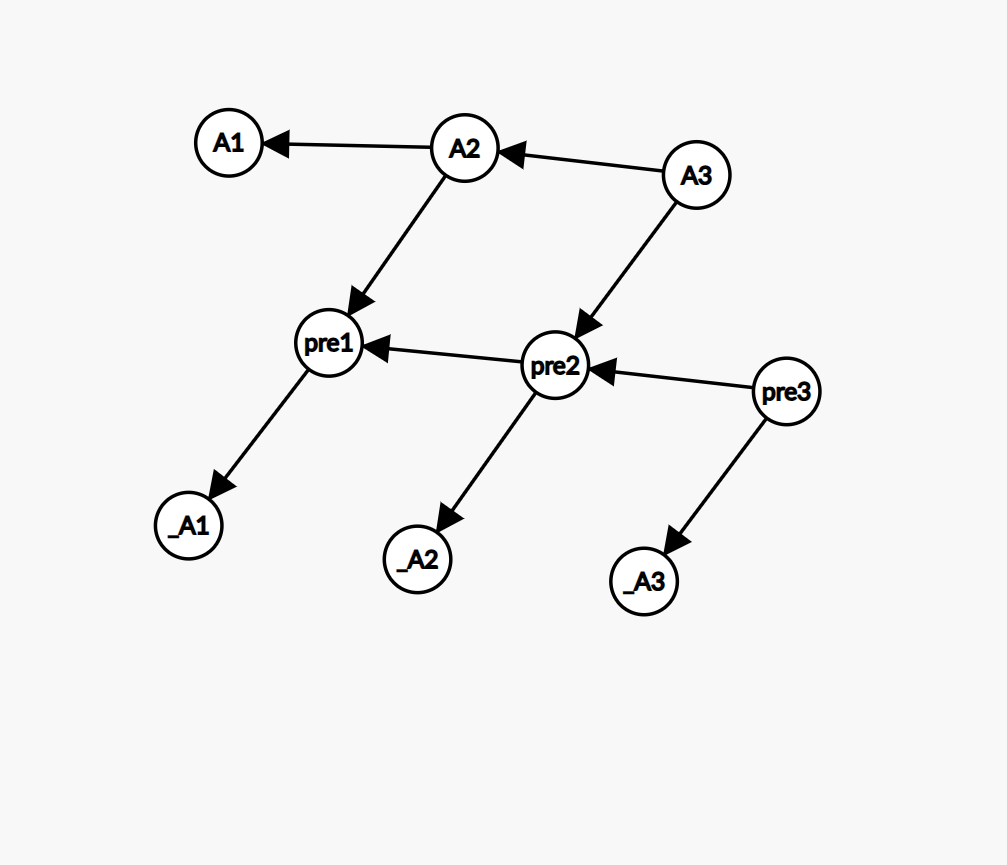
例如上图, A A A 值表示拥有这个键值的所有下标(前面下划线表示反变量) A 3 A_3 A3 需要连接 A ˉ 1 \bar A_1 Aˉ1 和 A ˉ 2 \bar A_2 Aˉ2,我们只需要将其连向 p r e 2 pre_2 pre2 : A 3 → p r e 2 A_3 \rarr pre_2 A3→pre2 就可以完成前缀的连边,同时 p r e 3 → A ˉ 3 pre_3 \rarr \bar A_3 pre3→Aˉ3, p r e 3 → p r e 2 pre_3 \rarr pre_2 pre3→pre2,以便后续相同键值的连边
后缀也是类似
需要注意的是:新建虚拟节点并不是严格按照正反变量的奇偶位置来排列的,而是紧挨着
所以我们判断可行解,只需要判断到 n n n 即可,否则会因为虚拟节点而干扰正确答案!
#include<bits/stdc++.h>
#define fore(i,l,r) for(int i=(int)(l);i<(int)(r);++i)
#define fi first
#define se second
#define endl '\n'
#define ull unsigned long long
#define sz(x) (int)x.size()const int INF=0x3f3f3f3f;
const long long INFLL=0x3f3f3f3f3f3f3f3fLL;typedef long long ll;struct TwoSat {int n; //属性数量std::vector<std::vector<int>> e;std::vector<bool> ans;TwoSat(int n) : n(n), e(2 * n), ans(n) {} //下标从0开始/* 建边表示 u为f 且 v为g */void addedge(int u, bool f, int v, bool g) { //原变量和反变量相邻放e[2 * u + !f].push_back(2 * v + g); //反变量在偶数位置,原变量在奇数位置e[2 * v + !g].push_back(2 * u + f);}bool satisfiable(int nn) {std::vector<int> id(2 * n, -1), dfn(2 * n, -1), low(2 * n, -1);std::vector<int> stk;int now = 0, cnt = 0;std::function<void(int)> tarjan = [&](int u) {stk.push_back(u);dfn[u] = low[u] = now++;for (auto v : e[u]) {if (dfn[v] == -1) {tarjan(v);low[u] = std::min(low[u], low[v]);} else if (id[v] == -1) {low[u] = std::min(low[u], dfn[v]);}}if (dfn[u] == low[u]) {int v;do {v = stk.back();stk.pop_back();id[v] = cnt;} while (v != u);++cnt;}};for (int i = 0; i < 2 * n; ++i) if (dfn[i] == -1) tarjan(i);for (int i = 0; i < nn; ++i) {if (id[2 * i] == id[2 * i + 1]) return false;ans[i] = id[2 * i] > id[2 * i + 1]; //取依赖性更高的那个}return true;}std::vector<bool> get_ans() { return ans; }
};const ll P = 1000001;
const int N = 200050;int yes(int x) {return 2 * x + 1;}
int no(int x) {return 2 * x;}int main(){std::ios::sync_with_stdio(false);std::cin.tie(nullptr);std::cout.tie(nullptr);int n;std::cin >> n;std::vector<int> a(n);TwoSat ts(2 * n + 2);fore(i, 0, n) std::cin >> a[i];int tot= 2 * n - 1;std::map<std::pair<int, int>, int> pre;std::map<std::pair<int, int>, int> suf;ts.e[0].push_back(1);ts.e[2 * n - 1].push_back(2 * n - 2);fore(i, 0, n){if(i > 0) ts.addedge(i - 1, 1, i, 1);if(i < n - 1) ts.addedge(i, 1, i + 1, 1);if(i < n - 1){if(pre.find({a[i], a[i + 1]}) != pre.end()){ts.e[2 * i + 1].push_back(pre[{a[i], a[i + 1]}]);ts.e[tot + 1].push_back(pre[{a[i], a[i + 1]}]);}pre[{a[i], a[i + 1]}] = ++tot;ts.e[tot].push_back(2 * i);}}for(int i = n - 2; i >= 0; --i){if(suf.find({a[i], a[i + 1]}) != suf.end()){ts.e[2 * i + 1].push_back(suf[{a[i], a[i + 1]}]);ts.e[tot + 1].push_back(suf[{a[i], a[i + 1]}]);}suf[{a[i], a[i + 1]}] = ++tot;ts.e[tot].push_back(2 * i);}if(!ts.satisfiable(n)){std::cout << "NO\n";return 0;}auto v = ts.get_ans();std::vector<int> ans;fore(i, 0, n - 1)if(v[i])ans.push_back(i + 1);std::cout << ans.size() << endl;for(auto i : ans) std::cout << i << ' ';std::cout << endl;return 0;
}/*
https://pintia.cn/problem-sets/1705510247604809728/exam/problems/1705514248467492866?type=7&page=0
*/
这篇关于2023ICPC网络预选赛 ( 2 ) (2) C.Covering【2-SAT、前后缀虚拟节点区间连边】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






