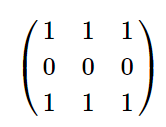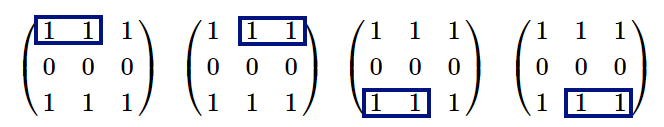Codeforces 1323B - Count Subrectangles

本文主要是介绍Codeforces 1323B - Count Subrectangles，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目链接

http://codeforces.com/problemset/problem/1323/B

题目描述

给出两个长度分别为 n, m 的数组 A，B，数组内的元素为 0 或 1。根据 A，B 构造矩阵 C，使 C 满足 $C_{i,j} = A_i * B_j$ 。显然，C中的元素也均为 0 或 1。
问，C 中有多少个子矩阵满足下述两个条件：

子矩阵一共包含 k 个元素。
子矩阵中的所有元素均为 1。

数据范围

$1\le n,m \le 40000,1 \le k \le n⋅m$

示例

n = 3 m = 3 k = 2
A = [1 0 1]
B = [1 1 1]
答案为 4。
矩阵 C 如下图：

四个满足要求的子矩阵，如下图：

解题思路

满足要求的子矩阵的行数和列数肯定都能整除 k。k 的除数肯定不会超过 $log_2^k + 1$ 个。
如果 A[i] = 0，矩阵 C 的第 i 行全为 0 。如果 A[i] = 1，矩阵 C 的第 i 行肯定就是 B 。

想明白上述问题之后，先来看下最朴素的解法：

枚举矩阵C的所有元素，将其作为子矩阵的右下角元素。该步骤时间复杂度为 O(n*m)。
位置锚定后，枚举子矩阵的长和宽。该步骤的时间复杂度为 O(k)。
判断子矩阵中的元素是否全为 1 。因为子矩阵面积为 k，所以该步骤时间复杂度亦为 O(k)。

上述算法的整体复杂度为 O(n*m*k*k)。

优化

先从最简单的第二步开始，如果预处理 k 的除数，该步骤的时间复杂度可以降到 $log_2^k$ 。因为 k 的除数不会超过 $log_2^k + 1$ 个。
此时，算法整体复杂度降到了 $O(n*m*k*log_2^k)$ 。

接下来观察一下矩阵 C，发现 C 的行很重复 —— 总是为 B 或者全为 0。那么应该可以用乘法代替步骤1，3的加法：
预处理 B 中满足下述要求的子区间的数量：

子区间的元素全为 1。
子区间的长度可以整除 k。

记 cb[i] 为满足上述要求的长度为 i 的区间的数量。这个步骤的时间复杂度可以做到 $O(m*log_2^k)$ 。

设结果为 res。
枚举数组 A 的位置 pos，并记录满足以 pos 为右端点，且元素全为 1 的子区间的最大长度，记为 len。那么有：
$\sum_{pos=1}^{n}\sum_{i=1}^{len_{pos}}cb[i]$
累加 cb[i] 的意义可以理解为：以矩阵 C 的第 pos 行中的某个元素为锚点的且列数为 cb[i] 的子矩阵的个数的累加和。
整体的时间复杂度可以做到 $O((n+m)*log_2^k)$ 。

代码

#include <bits/stdc++.h>using namespace std;map<int, int> dc;const int MAXN = 40001;
int a[MAXN], b[MAXN];int main() {cin.sync_with_stdio(false);int n, m, k;cin >> n >> m >> k;for(int i = 1; i <= n; i++) {cin >> a[i];}for(int i = 1; i <= m; i++) {cin >> b[i];}for(int i = max(n,m); i >= 1; i--) {if(k%i == 0) {dc.insert(make_pair(k/i, 0));}}for(int i = 1, c = 0; i <= m; i++) {if(b[i] == 1) {++c;for(auto it = dc.begin(); it != dc.end() && it->first <= c; it++) {it->second++;}} else {c = 0;}}int64_t res = 0;for(int i = 1, c = 0; i <= n; i++) {if(a[i] == 1) {++c;for(auto it = dc.cbegin(); it != dc.cend(); it++) {if(k/it->first <= c) {res += it->second;}}} else {c = 0;}}cout << res << endl;return 0;
}