纯小白蓝桥杯备赛笔记--DAY10（字符串）

2024-04-09 05:04
文章标签 笔记 字符串 day10 蓝桥 纯小白 杯备赛

本文主要是介绍纯小白蓝桥杯备赛笔记--DAY10（字符串），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

    • KMP字符串哈希
      • 算法简介：
      • 斤斤计较的小z--2047
      • 字符串hash
    • Manacher
      • 回文串的性质
      • 算法简介
      • 最长回文子串
    • 字典树基础
      • 朴素字符串查找
      • 步骤
      • 前缀判定--1204
    • 01tire
      • 算法简介：
      • 例题1：
      • 例题2：

KMP字符串哈希

算法简介：

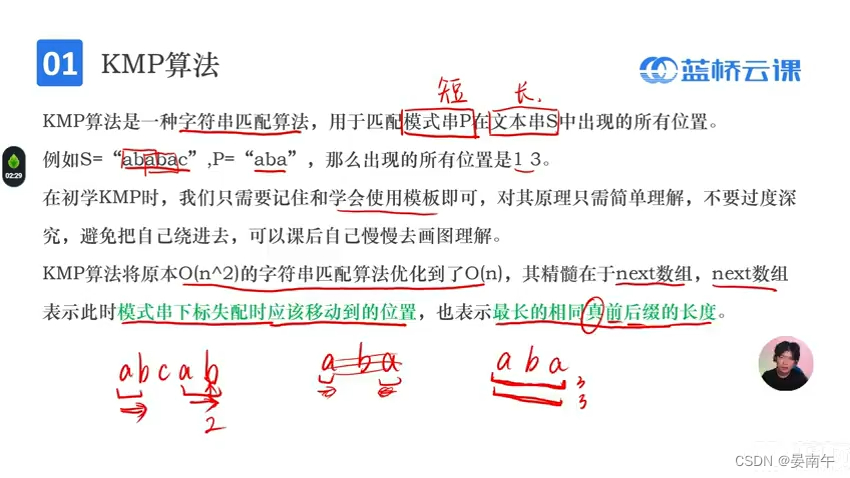
在这里插入图片描述

  • 真前后缀的意义：前后缀不相等。
  • 注意方向都是正向的，而不是回文的字符串。
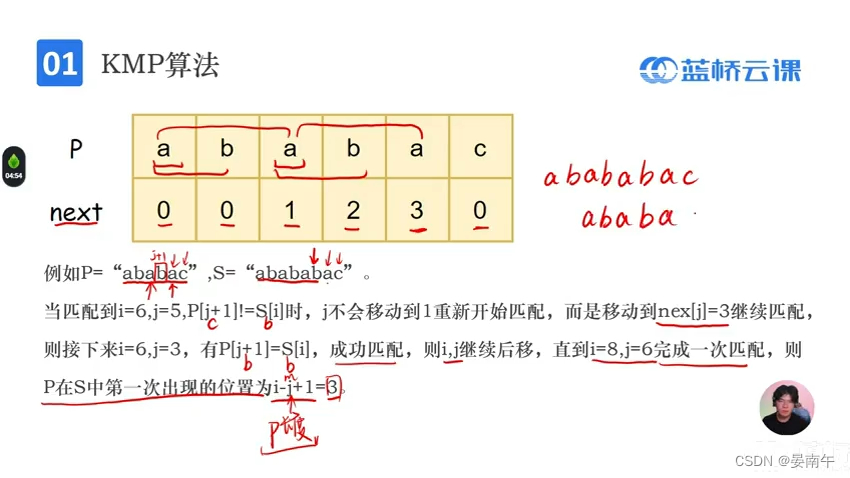
  • 在这里插入图片描述
  • 模版：
    在这里插入图片描述
char s[N],p[M];
int nex[M];
int n=strlen(s+1),m=strlen(p+1);//字符串的下标从1开始
nex[0]=nex[1]=0;
for(int i=2,j=0;i<m;i++)
{//不断匹配p[i]和p[j+1]while(j&&p[i]!=p[j+1])j=nex[j];if(p[i]==p[j+1])j++;//从while出来后要么j=0，要么匹配成功nex[i]=j; }
  • 用nex数组去匹配s
for(int i=1,j=0;i<=n;i++)
{
while(j&&s[i]!=p[j+1])j=nex[j];//失配时移动if(s[i]==p[j+1])j++;//成功匹配一个字符if(j==m)//成功匹配一次 
}

斤斤计较的小z–2047

在这里插入图片描述

#include<bits/stdc++.h>
using namespace std;const int N=1e6+9;
char s[N],p[N];
int nex[N];
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>p+1;int m=strlen(p+1);//模式串 cin>>s+1;int n=strlen(s+1);//文本串//get nextnex[0]=nex[1]=0;for(int i=2,j=0;i<=m;i++){while(j&&p[i]!=p[j+1])j=nex[j];if(p[i]==p[j+1])j++;nex[i]=j;} //对s串进行匹配int ans=0;for(int i=1,j=0;i<=n;i++){while(j&&s[i]!=p[j+1])j=nex[j];if(s[i]==p[j+1])j++;if(j==m)ans++;} cout<<ans<<endl;return 0;}

定义了一个字符数组s和p，分别用于存储文本串和模式串。同时定义了一个整数数组nex，用于存储模式串的next数组。
通过cin读取输入的模式串和文本串，并计算它们的长度。
初始化nex数组的前两个元素为0。
使用循环计算模式串的next数组。next数组用于记录模式串中每个位置之前的子串的最长公共前后缀长度。具体计算过程如下：
初始化指针j为0。
从模式串的第三个字符开始遍历，对于每个位置i：
如果当前字符与j+1位置的字符不相等，将j更新为nex[j]，即向前回溯到上一个匹配的位置。
如果当前字符与j+1位置的字符相等，将j加1。
将nex[i]更新为j，表示当前位置之前的子串的最长公共前后缀长度。
初始化变量ans为0，用于记录模式串在文本串中的出现次数。
使用循环对文本串进行匹配：
初始化指针j为0。
从文本串的第一个字符开始遍历，对于每个位置i：
如果当前字符与j+1位置的字符不相等，将j更新为nex[j]，即向前回溯到上一个匹配的位置。
如果当前字符与j+1位置的字符相等，将j加1。
如果j等于模式串的长度，说明找到了一个匹配，将ans加1。
输出结果ans，即模式串在文本串中的出现次数。

字符串hash

在这里插入图片描述

  • 进制数一般是一个质数。
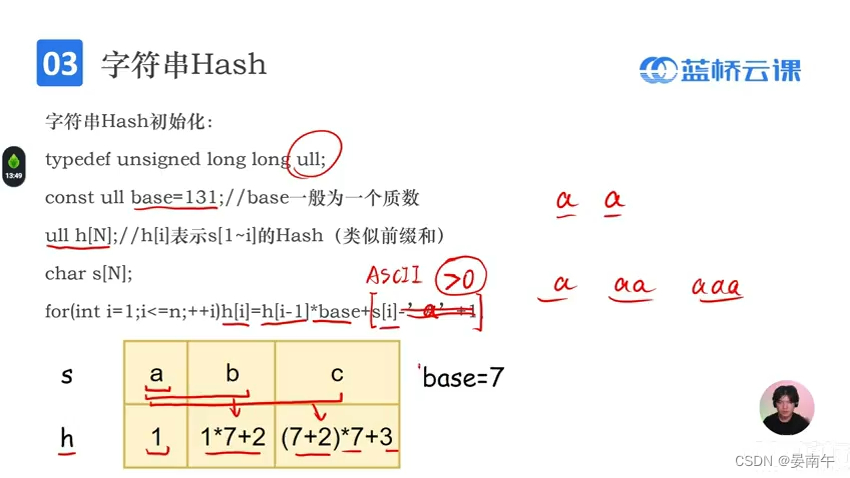
  • hash的初始化在这里插入图片描述
  • 获取子串：
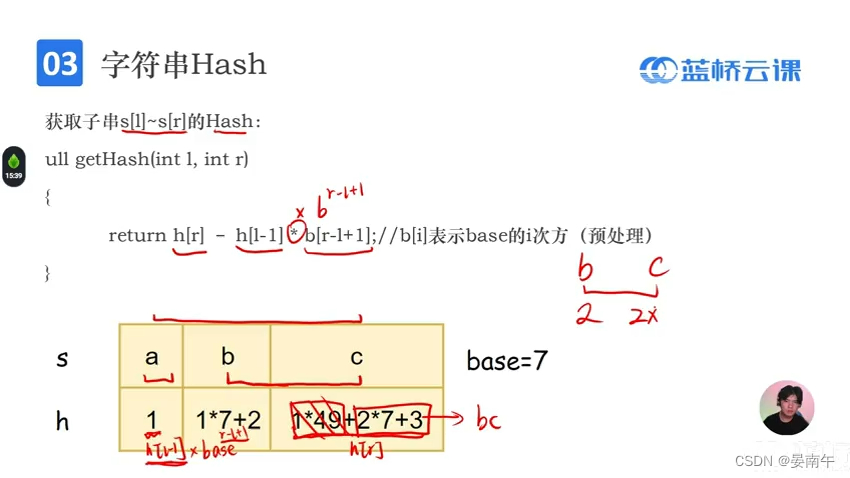
    在这里插入图片描述
#include<bits/stdc++.h>
using namespace std;const int N=1e6+9;
char s[N],p[N];
typedef unsigned long long ull;
const ull base =131;
int l,r;
ull h1[N],h2[N],b[N];//b数组用来存储base的多少次方 
ull getHash(ull h[],int l,int r)
{return h[r]-h[l-1]*b[r-l+1];
}
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>p+1;int m=strlen(p+1);//模式串 cin>>s+1;int n=strlen(s+1);//文本串b[0]=1;//预处理b数组 for(int i=1;i<=n;i++){b[i]=b[i-1]*base;h1[i]=h1[i-1]*base+(int)p[i]; h2[i]=h2[i-1]*base+(int)s[i]; }//开始枚举int ans=0;for(int i=1;i+m-1<=n;i++){if(getHash(h1,l,m)==getHash(h2,i,i+m-1))ans++;} cout<<ans<<endl;return 0;}

Manacher

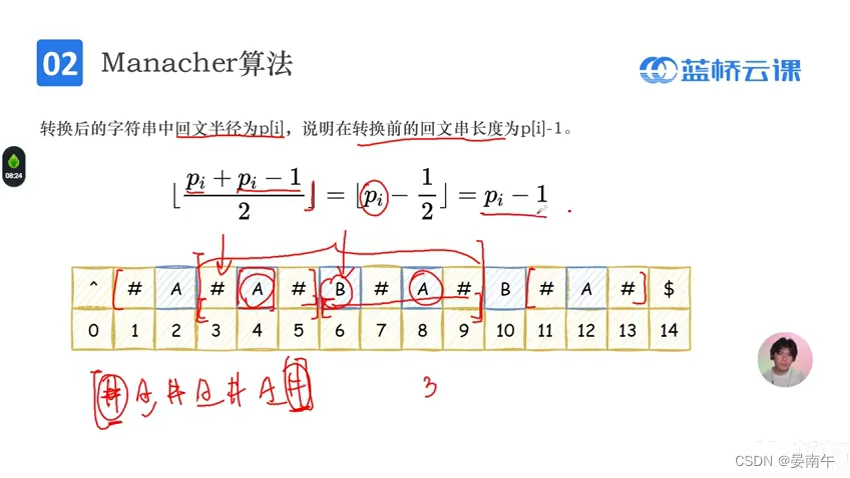
回文串的性质

在这里插入图片描述

  • manacher解决偶数个字符组成的字符串没有回文半径的问题。
  • 回文的额递归性质要理解一下。

算法简介

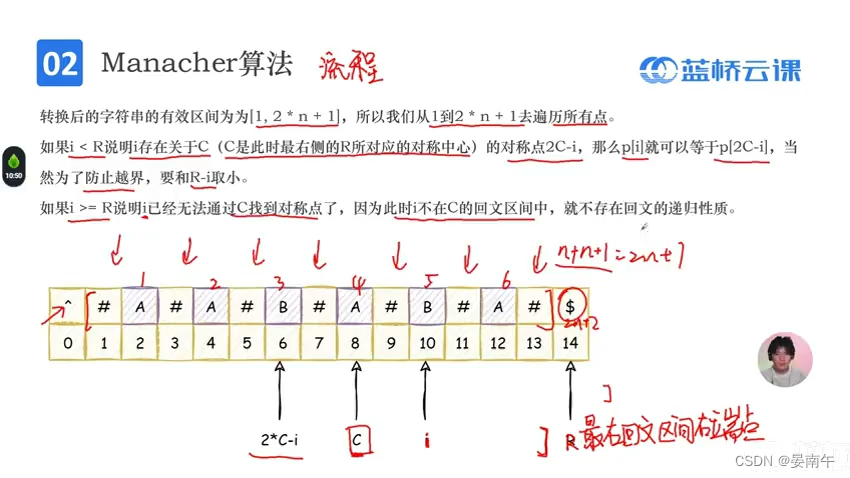
在这里插入图片描述
在这里插入图片描述

  • 算法流程：
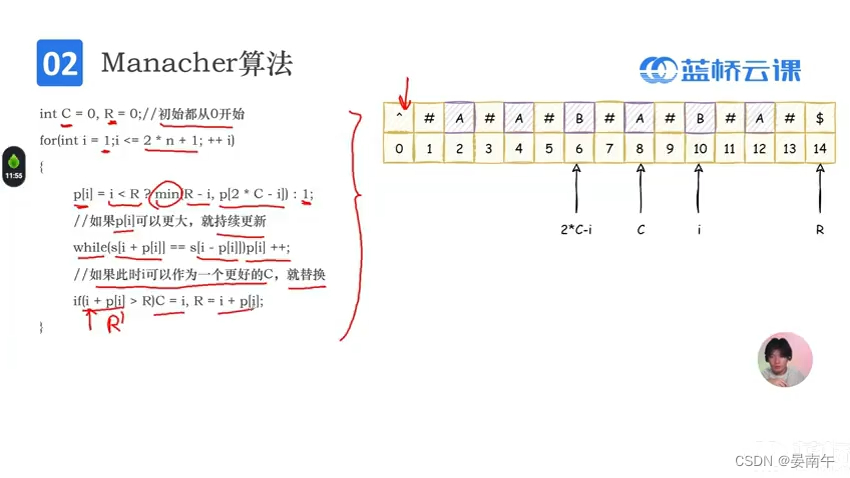
    在这里插入图片描述
  • 流程：
    在这里插入图片描述

最长回文子串

#include<bits/stdc++.h>
using namespace std;const int N=1e6+9;//注意空间要开二倍 
char s[N];
int p[N];
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>s+1;int n=strlen(s+1);//添加特殊字符 for(int i=2*n+1;i>=1;i--)s[i]=(i&1)?'#':s[i>>1];s[0]='^',s[2*n+2]='$';int c=0,r=0;for(int i=1;i<=2*n+1;i++){p[i]=i<r?min(r-1,p[2*c-i]):1;while(s[i+p[i]]==s[i-p[i]])p[i]++;if(i+p[i]>r)c=i,r=i+p[i];}int ans=0;for(int i=1;i<=2*n+1;i++)ans=max(ans,p[i]-1);cout<<ans<<endl;return 0;}

字典树基础

朴素字符串查找

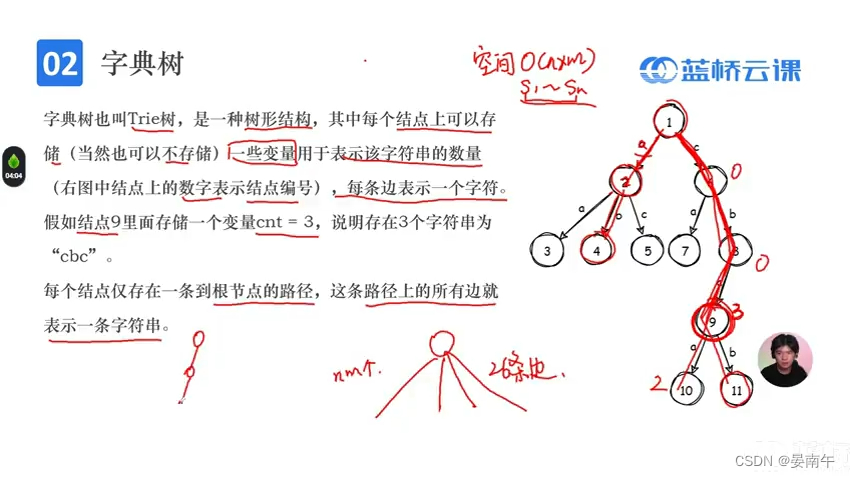
在这里插入图片描述
在这里插入图片描述

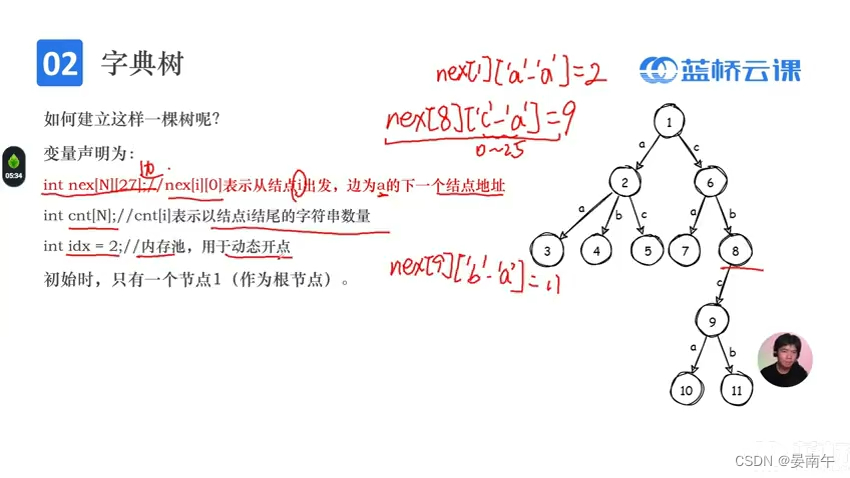
  • 如何建立一个树：在这里插入图片描述

步骤

  • 变量的声明：
int nex[N][27];//表示从节点i出发，下一个节点地址 
int cnt[N];//以i结尾的字符串的数量 
int idx=2; //内存池，用作动态开点
  • 编写insert函数，用于将一个字符串s加入进去
void insert(char s[])
{int n=strlen(s+1);int x=1;//根结点for(int i=1;i<=n;i++){//先检查x是否存在s[i]的边if(!nex[x][s[i]-'a']) nex[x][s[i]-'a']=idx++;x=nex[x][s[i]-'a'];//x移动到新点上 } cnt[x]++;}
  • 编写check函数，用于判断某个字符串在trie中出现的次数
int check(char s[])
{int n=strlen(s+1);int x=1;for(int i=1;i<=n;i++)x=nex[x][s[i]-'a'];return cnt[x]; 
}

前缀判定–1204

  1. 这么多字符串都要一一存入吗？
    不需要。每一个直接存入tire中。注意一个细节，要么都是从0开始计数，要么都是从1开始计数。

#include<bits/stdc++.h>
using namespace std;
const int N =2e6+9;
//声明变量
int nex[N][26];
int cnt[N];
int idx=2;//1已经当做根使用void insert(char s[])
{int x=1;//设置根结点，从此开始for(int i=0;s[i];i++)//这里的条件：字符串以\0结尾，s[i]表达的是不为0 {//判断x是否存在s[i]这条边if(!nex[x][s[i]-'a'])nex[x][s[i]-'a'] =idx++;x=nex[x][s[i]-'a'];} cnt[x]++;
}
bool check(char s[])
{int x=1;for(int i=0;s[i];i++){x=nex[x][s[i]-'a'];}return x;
}int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int n,m;cin>>n>>m;for(int i=1;i<=n;i++){char s[N];cin>>s;insert(s);}for(int i=1;i<=m;i++){char s[N];cin>>s;cout<<(check(s)?'Y':'N')<<endl;}	return 0;
}
  • 这里再粘贴来自蓝桥–冯勒布的代码以理解：
//本题是一道字典树的模板题
//字典树是一种高效率存储多个字符串的数据结构
//其每个结点的权值代表以该结点结尾的字符串的数量,每条边存储一个字符
//从根结点开始,按某一路径遍历到某一结点,即得到一种字符串,其个数等于当前结点存储的数值
//如从根结点开始,依次走过'a''b''c'三条边到达9号结点,9号结点保存的数字是3
//则得到字符串"abc",其数量为3个 
#include <bits/stdc++.h>using namespace std;const int N=2e6+100;int nex[N][27];//nex[i][0]表示从结点i出发,边为'a'的下一个结点地址(假设字符串全由小写字母构成)
//如1号结点与2号结点间存在一条记录字母'a'的边,则nex[1]['a'-'a']=2 
//如8号结点与9号结点间存在一条记录字母'c'的边,则nex[8]['c'-'a']=9 
int cnt[N];//cnt[i]表示以结点i结尾的字符串的数量,即每个结点的权值 
int idx=2;//用于动态开点,初始时只有一个根结点1 void insert(char *S)//在字典树中插入字符串S的信息 
{int x=1;//x表示结点编号,初始从根结点(1号)开始 for(int i=0;S[i]!='\0';i++)//遍历字符串S {//先检查x是否存在S[i]的边 if(nex[x][S[i]-'a']==0)//从结点x出发,目前还没有记录当前字母的边 {nex[x][S[i]-'a']=idx++;//则新建一个边记录之,同时动态开点 }x=nex[x][S[i]-'a'];//到达下一个结点编号}    //cnt[x]++;//最终x到达字符串末尾字符对应的结点上,其计数值加1 
}bool check(char *T)//在字典树中查找字符串T(计算出现的次数)
{int x=1;//x表示结点编号,初始从根结点(1号)开始 for(int i=0;T[i]!='\0';i++)//遍历字符串T {x=nex[x][T[i]-'a'];//根据当前字符,x不断向下追溯,最终到达结尾//若不存在这个字符(记录这个字符的边),则x=0,后续x将一直为0 }    //return cnt[x];//返回字符串T出现的次数,即结尾字符对应的结点所记录的权值 return x;//本题返回x即可,只需判断x是否为0 
}int main()
{int n,m;cin>>n>>m;while(n--)//N个字符串 {char S[N];cin>>S;insert(S);//每输入一个字符串,就将其信息插入字典树 }    while(m--)//M个询问 {char T[N];cin>>T;if(check(T))cout<<"Y"<<endl;//在字典树中找到T,输出Y else cout<<"N"<<endl;//没找到,输出N }return 0;
}

01tire

算法简介：

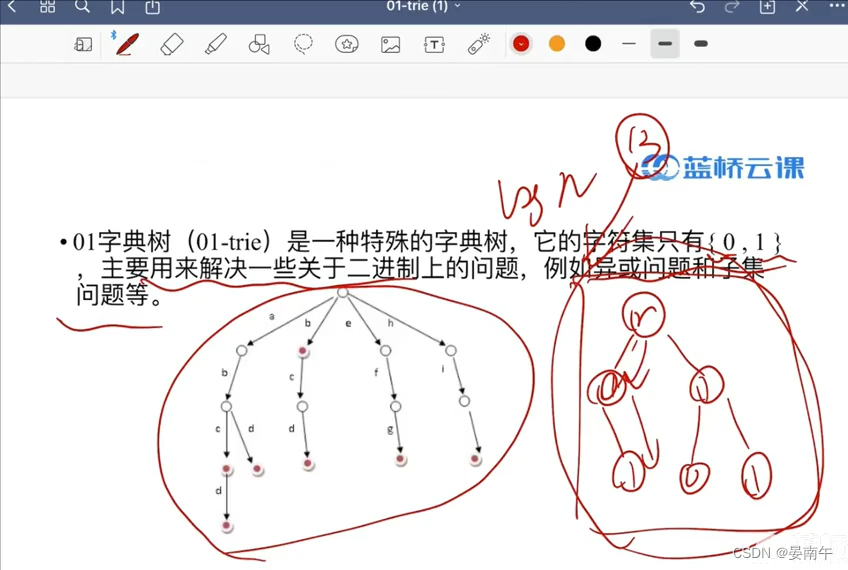
在这里插入图片描述

  • 解决思想：结点只能为0和1。
  • 解决问题：二进制问题。例如：异或问题和子集问题。

例题1：

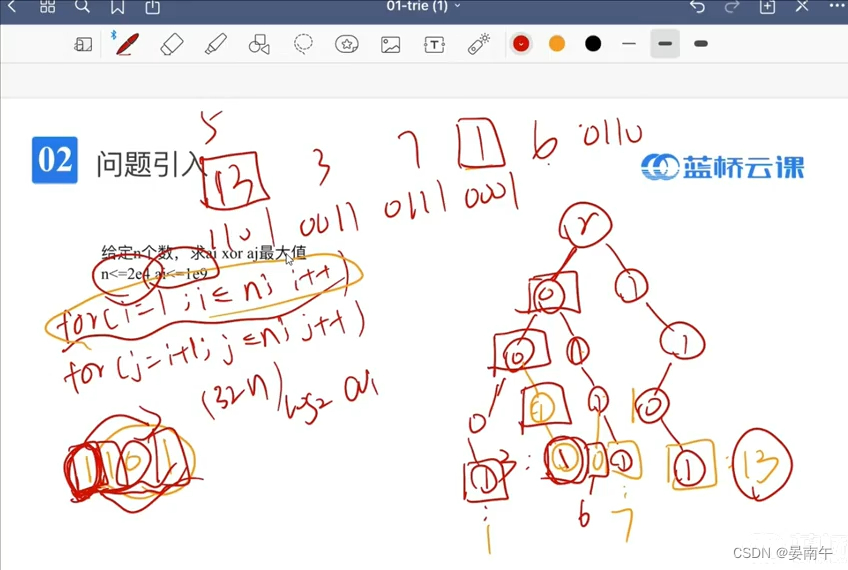
在这里插入图片描述

  • 怎么通过01树判断数字的大小呢？
    • 高位往低位建立01tire树。
    • 使用逐位确定的方法：对于权值较大的数，优先保证其“1”不变。
    • 例如：1101。对于第一位1，优先往0的方向走，对于0，优先往1的方向走。这样找出和13异或最大的数为6。
    • 实际上，高位的权值大于低位的权值和。
  • 为什么不采用两层for循环？
    • 根据题目中给出的条件，可以看出时间复杂度是超过的。
  • 时间复杂度？
    log(n)
#include<bits/stdc++.h>
using namespace std;
const int N =210000;
int ch[N][2],val[N],n,ans,tot;
int a[N];
void insert(int x)
{int now=0;for(int j=31;j>=0;j--){int pos=((x>>j)&1);//拆分一下二进制 if(!ch[now][pos])ch[now][pos]=++tot;now=ch[now][pos];}val[now]=x;return ;
}
int query(int x)
{int now=0;for(int j=31;j>=0;j--){int pos=((x>>j)&1);//拆分一下二进制 if(ch[now][pos^1])now=ch[now][pos^1];//如果1存在，往0的方向去走 now=ch[now][pos];}    return val[now]; 
}
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n;i++){int x;cin>>x;a[i]=x;insert(x);}for(int i=1;i<=n;i++){ans=max(ans,query(a[i]));} cout<<ans<<endl;return 0;
}
  • 总结：
    在这里插入图片描述

例题2：

在这里插入图片描述

  • 拆分：dfs处理出根节点到其他两个点的异或值。
  • 把这些点放到tire树中就变成了上面那道题。
  • 代码：
#include<bits/stdc++.h>
using namespace std;
const int N =110000;
int tire[N*30][2],val[N],n,ans,rt,cnt,head[N],tot;
int xo[N];
struct Edge
{int nex,to,dis;}edge[N<<1];
//加边
void add(int from,int to,int dis)
{edge[++cnt].nex=head[from];head[from]=cnt;edge[cnt].to=to;edge[cnt].dis=dis;return ;} void dfs(int x,int fa){for(int i=head[x];i;i=edge[i].nex){int v=edge[i].to;if(v==fa)continue;xo[v]=xo[x]^edge[i].dis;dfs(v,x);}return ;}
void insert(int x)
{int now=0;for(int j=31;j>=0;j--){int pos=((x>>j)&1);//拆分一下二进制 if(!tire[now][pos])tire[now][pos]=++tot;now=tire[now][pos];}val[now]=x;return ;
}
int query(int x)
{int now=0;for(int j=31;j>=0;j--){int pos=((x>>j)&1);//拆分一下二进制 if(tire[now][pos^1])now=tire[now][pos^1];//如果1存在，往0的方向去走 now=tire[now][pos];}    return val[now]; 
}
int main()
{ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n;i++){int u,v,w;cin>>u>>v>>w;add(u,v,w);add(v,u,w);}dfs(1,0);//把这些东西都插入到tire树中for(int i=1;i<=n;i++)insert(xo[i]); for(int i=1;i<=n;i++){ans=max(ans,query(xo[i]));} cout<<ans<<endl;return 0;
}
  • 总结：dfs处理出根节点到所有节点的边权异或值，随后把它们扔进 o1Trie中。
  • 为了让异或值最大，我们可以枚举节点，在Trie上贪心：从高到低位，尽量选和当前数二进制位不一样的，随后再与原节点异或值异或一下，取max.

这篇关于纯小白蓝桥杯备赛笔记--DAY10（字符串）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/887238。

相关文章

C#数据结构之字符串(string)详解

C#数据结构之字符串(string)详解

《C#数据结构之字符串(string)详解》：本文主要介绍C#数据结构之字符串(string),具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录转义字符序列字符串的创建字符串的声明null字符串与空字符串重复单字符字符串的构造字符串的属性和常用方法属性常用方法总结摘
阅读更多...
Java实现时间与字符串互相转换详解

Java实现时间与字符串互相转换详解

《Java实现时间与字符串互相转换详解》这篇文章主要为大家详细介绍了Java中实现时间与字符串互相转换的相关方法,文中的示例代码讲解详细,感兴趣的小伙伴可以跟随小编一起学习一下... 目录一、日期格式化为字符串（一）使用预定义格式（二）自定义格式二、字符串解析为日期（一）解析ISO格式字符串（二）解析自定义
阅读更多...
python中字符串拼接的几种方法及优缺点对比详解

python中字符串拼接的几种方法及优缺点对比详解

《python中字符串拼接的几种方法及优缺点对比详解》在Python中,字符串拼接是常见的操作,Python提供了多种方法来拼接字符串,每种方法有其优缺点和适用场景,以下是几种常见的字符串拼接方法,需... 目录1. 使用 + 运算符示例：优缺点：2. 使用&nbsjsp;join() 方法示例：优缺点：3
阅读更多...
java字符串数字补齐位数详解

java字符串数字补齐位数详解

《java字符串数字补齐位数详解》：本文主要介绍java字符串数字补齐位数,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录Java字符串数字补齐位数一、使用String.format()方法二、Apache Commons Lang库方法三、Java 11+的St
阅读更多...
C++字符串提取和分割的多种方法

C++字符串提取和分割的多种方法

《C++字符串提取和分割的多种方法》在C++编程中,字符串处理是一个常见的任务,尤其是在需要从字符串中提取特定数据时,本文将详细探讨如何使用C++标准库中的工具来提取和分割字符串,并分析不同方法的适用... 目录1. 字符串提取的基本方法1.1 使用 std::istringstream 和 >> 操作符示
阅读更多...
C语言字符函数和字符串函数示例详解

C语言字符函数和字符串函数示例详解

《C语言字符函数和字符串函数示例详解》本文详细介绍了C语言中字符分类函数、字符转换函数及字符串操作函数的使用方法,并通过示例代码展示了如何实现这些功能,通过这些内容,读者可以深入理解并掌握C语言中的字... 目录一、字符分类函数二、字符转换函数三、strlen的使用和模拟实现3.1strlen函数3.2st
阅读更多...
Java反转字符串的五种方法总结

Java反转字符串的五种方法总结

《Java反转字符串的五种方法总结》：本文主要介绍五种在Java中反转字符串的方法,包括使用StringBuilder的reverse()方法、字符数组、自定义StringBuilder方法、直接... 目录前言方法一：使用StringBuilder的reverse()方法方法二：使用字符数组方法三：使用自
阅读更多...
Golang中拼接字符串的6种方式性能对比

Golang中拼接字符串的6种方式性能对比

《Golang中拼接字符串的6种方式性能对比》golang的string类型是不可修改的,对于拼接字符串来说,本质上还是创建一个新的对象将数据放进去,主要有6种拼接方式,下面小编就来为大家详细讲讲吧... 目录拼接方式介绍性能对比测试代码测试结果源码分析golang的string类型是不可修改的，对于拼接字
阅读更多...
Java对象和JSON字符串之间的转换方法(全网最清晰)

Java对象和JSON字符串之间的转换方法(全网最清晰)

《Java对象和JSON字符串之间的转换方法(全网最清晰)》：本文主要介绍如何在Java中使用Jackson库将对象转换为JSON字符串,并提供了一个简单的工具类示例,该工具类支持基本的转换功能,... 目录前言1. 引入 Jackson 依赖2. 创建 jsON 工具类3. 使用示例转换 Java 对象为
阅读更多...
golang字符串匹配算法解读

golang字符串匹配算法解读

《golang字符串匹配算法解读》文章介绍了字符串匹配算法的原理,特别是Knuth-Morris-Pratt（KMP）算法,该算法通过构建模式串的前缀表来减少匹配时的不必要的字符比较,从而提高效率,在... 目录简介KMP实现代码总结简介字符串匹配算法主要用于在一个较长的文本串中查找一个较短的字符串（称为
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2