本文主要是介绍蓝桥杯第十四届C++C组,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
三国游戏
填充
翻转
【单调队列优化DP】子矩阵
【快速幂、欧拉函数】互质数的个数
【tire树】异或和之差
【质因数分解】公因数匹配
子树的大小
三国游戏
题目描述
小蓝正在玩一款游戏。游戏中魏蜀吴三个国家各自拥有一定数量的士兵X, Y, Z (一开始可以认为都为 0 )。游戏有 n 个可能会发生的事件,每个事件之间相互独立且最多只会发生一次,当第 i 个事件发生时会分别让 X, Y, Z 增加Ai , Bi ,Ci 。
当游戏结束时 (所有事件的发生与否已经确定),如果 X, Y, Z 的其中一个大于另外两个之和,我们认为其获胜。例如,当 X > Y + Z 时,我们认为魏国获胜。小蓝想知道游戏结束时如果有其中一个国家获胜,最多发生了多少个事件?
如果不存在任何能让某国获胜的情况,请输出 −1 。
输入格式
输入的第一行包含一个整数 n 。
第二行包含 n 个整数表示 Ai,相邻整数之间使用一个空格分隔。
第三行包含 n 个整数表示 Bi,相邻整数之间使用一个空格分隔。
第四行包含 n 个整数表示 Ci,相邻整数之间使用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
样例输入
3 1 2 2 2 3 2 1 0 7
样例输出
2
提示
发生两个事件时,有两种不同的情况会出现获胜方。
发生 1, 2 事件时蜀国获胜。
发生 1, 3 事件时吴国获胜。
对于 40% 的评测用例,n ≤ 500 ;
对于 70% 的评测用例,n ≤ 5000 ;
对于所有评测用例,1 ≤ n ≤ 10^5,1 ≤ Ai , Bi ,Ci ≤ 10^9 。
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1e5+10;
typedef long long LL;
LL a[N],b[N],c[N],d[N];
int n;
int get(LL x[],LL y[],LL z[]){memset(d,0,sizeof d);for(int i=1;i<=n;i++) d[i]=x[i]-(y[i]+z[i]);sort(d+1,d+1+n);LL t=-1;LL sum=0;for(int i=n;i>=1;i--){sum+=d[i];if(sum>0){t=n-i+1;}else{return t;}}
}
int main(){cin>>n;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) cin>>b[i];for(int i=1;i<=n;i++) cin>>c[i];int maxv=-1;maxv=max(maxv,get(a,b,c));maxv=max(maxv,get(b,a,c));maxv=max(maxv,get(c,a,b));cout<<maxv<<endl;return 0;
}填充
题目描述
有一个长度为 n 的 01 串,其中有一些位置标记为 ?,这些位置上可以任意填充 0 或者 1,请问如何填充这些位置使得这个 01 串中出现互不重叠的 00 和 11 子串最多,输出子串个数。
输入格式
输入一行包含一个字符串。
输出格式
输出一行包含一个整数表示答案。
样例输入
1110?0
样例输出
2
提示
如果在问号处填 0 ,则最多出现一个 00 和一个 11:111000 。
对于所有评测用例,1 ≤ n ≤ 1000000 。
#include<iostream>
using namespace std;
int main(){string s;cin>>s;int cnt=0;for(int i=1;i<s.size();i++){if(s[i]==s[i-1]||s[i-1]=='?'||s[i]=='?'){cnt++;i++;}}cout<<cnt<<endl;return 0;
}翻转
题目描述
小蓝用黑白棋的 n 个棋子排成了一行,他在脑海里想象出了一个长度为 n 的 01 串 T,他发现如果把黑棋当做 1,白棋当做 0,这一行棋子也是一个长度为 n 的 01 串 S。
小蓝决定,如果在 S 中发现一个棋子和它两边的棋子都不一样,就可以将其翻转变成另一个颜色。也就是说,如果 S 中存在子串 101 或者 010,就可以选择将其分别变为 111 和 000,这样的操作可以无限重复。
小蓝想知道最少翻转多少次可以把 S 变成和 T 一模一样。
输入格式
输入包含多组数据。
输入的第一行包含一个正整数 D 表示数据组数。
后面 2D 行每行包含一个 01 串,每两行为一组数据,第 2i − 1 行为第 i 组
数据的 Ti,第 2i 行为第 i 组数据的 Si,Si 和 Ti 长度均为 ni。
输出格式
对于每组数据,输出一行包含一个整数,表示答案,如果答案不存在请输出 −1。
样例输入
2 1000111 1010101 01000 11000
样例输出
2 -1
提示
对于 20% 的评测用例,1 ≤ ni ≤ 10 ;
对于所有评测用例,保证 1 ≤ ni ≤ 10^6 ,ni > 0 。
#include<iostream>
using namespace std;
int n;
string t,s;
bool check(int i){if(i==0||i==n-1) return 0;if(s[i-1]==t[i-1]&&s[i+1]==t[i+1]&&s[i-1]==s[i+1]&&s[i]!=s[i-1]) return 1;return 0;}
int main(){int T;cin>>T;while(T--){cin>>t>>s;n=s.size();bool flag=1;int cnt=0;for(int i=0;i<n;i++){if(s[i]!=t[i]){if(check(i)) cnt++;else {flag=0;break;}}}if(flag) cout<<cnt<<endl;else cout<<"-1"<<endl;}return 0;
}【单调队列优化DP】子矩阵
题目描述
给定一个 n × m (n 行 m 列)的矩阵。
设一个矩阵的价值为其所有数中的最大值和最小值的乘积。求给定矩阵的所有大小为 a × b (a 行 b 列)的子矩阵的价值的和。
答案可能很大,你只需要输出答案对 998244353 取模后的结果。
输入格式
输入的第一行包含四个整数分别表示 n, m, a, b ,相邻整数之间使用一个空格分隔。
接下来 n 行每行包含 m 个整数,相邻整数之间使用一个空格分隔,表示矩阵中的每个数 Ai, j 。
输出格式
输出一行包含一个整数表示答案。
样例输入
2 3 1 2 1 2 3 4 5 6
样例输出
58
提示
1×2+2×3+4×5+5×6 = 58 。
对于 40% 的评测用例,1 ≤ n, m ≤ 100 ;
对于 70% 的评测用例,1 ≤ n, m ≤ 500 ;
对于所有评测用例,1 ≤ a ≤ n ≤ 1000 1 ≤ b ≤ m ≤ 1000 1 ≤ Ai, j ≤ 10^9 。
#include<iostream>
#include<deque>
#include<cstring>
using namespace std;
typedef long long LL;
const int N=1010;
LL g[N][N],minv[N][N],maxv[N][N];
LL a[N],b[N],c[N];
int n,m,x,y;
void get_max(LL a[],LL b[],int n,int k){deque<int> q;q.push_back(0);for(int i=1;i<=n;i++){while(q.size()&&a[q.back()]<=a[i]) q.pop_back();q.push_back(i);while(q.size()&&i-q.front()>=k) q.pop_front();b[i]=a[q.front()];}
}
void get_min(LL a[],LL b[],int n,int k){deque<int> q;q.push_back(0);for(int i=1;i<=n;i++){while(q.size()&&a[q.back()]>=a[i]) q.pop_back();q.push_back(i);while(q.size()&&i-q.front()>=k) q.pop_front();b[i]=a[q.front()];}
}
int main(){cin>>n>>m>>x>>y;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){cin>>g[i][j];}}for(int i=1;i<=n;i++){get_max(g[i],maxv[i],m,y);get_min(g[i],minv[i],m,y);}LL sum=0;for(int j=y;j<=m;j++){for(int i=1;i<=n;i++) c[i]=maxv[i][j];get_max(c,a,n,x);for(int i=1;i<=n;i++) c[i]=minv[i][j];get_min(c,b,n,x);for(int i=x;i<=n;i++){sum=(sum+(a[i]*b[i])%998244353)%998244353;}}cout<<sum<<endl;return 0;
}【快速幂、欧拉函数】互质数的个数
给定 a, b,求 1 ≤ x < a^b 中有多少个 x 与 a^b 互质。由于答案可能很大,你只需要输出答案对 998244353 取模的结果。
输入格式
输入一行包含两个整数分别表示 a, b,用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
样例输入
2 5
样例输出
16
提示
对于 30% 的评测用例,a^b ≤ 10^6 ;
对于 70% 的评测用例,a ≤ 106,b ≤ 10^9 ;
对于所有评测用例,1 ≤ a ≤ 10^9,1 ≤ b ≤ 101^8 。
#include<iostream>
using namespace std;
typedef long long LL;
const int mod=998244353;
LL quick_pow(LL a,LL b){LL res=1;while(b){if(b&1) res=res*a%mod;a=a*a%mod;b>>=1;}return res;
}
LL eu(LL n){LL res=n;for(LL i=2;i<=n/i;i++){if(n%i==0){res=res*(i-1)/i%mod;while(n%i==0) n/=i;}}if(n>1) res=res*(n-1)/n%mod;return res;
}
int main(){LL a,b;cin>>a>>b;LL n=quick_pow(a,b);cout<<eu(n)%mod<<endl;return 0;
}【tire树】异或和之差
题目描述
给定一个含有 n 个元素的数组 Ai,你可以选择两个不相交的子段。求出这两个子段内的数的异或和的差值的最大值。
输入格式
输入的第一行包含一个整数 n 。
第二行包含 n 个整数 Ai ,相邻整数之间使用一个空格分隔。
输出格式
输出一行包含一个整数表示答案。
样例输入
6 1 2 4 9 2 7
样例输出
14
提示
两个子段可以分别选 1 和 4,9,2,差值为 15 − 1 = 14 。
对于 40% 的评测用例,n ≤ 5000 ;
对于所有评测用例,2 ≤ n ≤ 2 × 10^5,0 ≤ Ai ≤ 2^20 。
区间 [l,r] 异或和最大就相当于 最大,即从异或前缀和 s 中找到两个数异或最大,异或和最小同理。
#include<iostream>
#include<vector>
#include<cstring>
#include<map>
#define int long long
using namespace std;
const int N=2e5+10,M=4e6+10;
int son[M][2];
int idx=0;
int a[N];
int lmx[N],lmi[N],rmx,rmi=2e9;
void insert(int x){int p=0;for(int i=20;i>=0;i--){int u=x>>i&1;if(!son[p][u]){son[p][u]=++idx;}p=son[p][u];}
}
//求异或最大需要尽可能多 不相同 的位数
int query_max(int x){int p=0;int res=0;for(int i=20;i>=0;i--){int u=x>>i&1;if(son[p][!u]){res+=1<<i;p=son[p][!u];}else{p=son[p][u];}}return res;
}
//求异或最小需要尽可能多 相同 的位数
int query_min(int x){int p=0,res=0;for(int i=20;i>=0;i--){int u=x>>i&1;if(son[p][u]){p=son[p][u];}else{res+=1<<i;p=son[p][!u];}}return res;
}
signed main(){int n;cin>>n;int maxv=0;for(int i=1;i<=n;i++){cin>>a[i];}int sum=0;//异或前缀和insert(sum);lmx[0]=0,lmi[0]=2e9;for(int i=1;i<=n;i++){sum^=a[i];//前i中最大(最小)的区间异或和lmx[i]=max(lmx[i-1],query_max(sum));lmi[i]=min(lmi[i-1],query_min(sum));insert(sum);//构造树}memset(son,0,sizeof son);sum=0;idx=0;insert(sum);int res=0;for(int i=n;i>=1;i--){sum^=a[i];rmx=max(rmx,query_max(sum));rmi=min(rmi,query_min(sum));res=max(max(res,lmx[i-1]-rmi),rmx-lmi[i-1]);insert(sum);}cout<<res<<endl;return 0;
}【质因数分解】公因数匹配
题目描述
给定 n 个正整数 Ai,请找出两个数 i, j 使得 i < j 且 Ai 和 Aj 存在大于 1 的公因数。
如果存在多组 i, j,请输出 i 最小的那组。如果仍然存在多组 i, j,请输出 i 最小的所有方案中 j 最小的那组。
输入格式
输入的第一行包含一个整数 n。
第二行包含 n 个整数分别表示 A1 A2 · · · An,相邻整数之间使用一个空格分隔。
输出格式
输出一行包含两个整数分别表示题目要求的 i, j,用一个空格分隔。
样例输入
5 5 3 2 6 9
样例输出
2 4
提示
对于 40% 的评测用例,n ≤ 5000 ;
对于所有评测用例,1 ≤ n ≤ 105,1 ≤ Ai ≤ 106 。
#include<iostream>
#include<vector>
#include<map>
#define int long long
using namespace std;
const int N=1e5+10;
int a[N];
map<int,int> mp;//存储每个质因子第一次出现的位置
int get(int i){int pos=1e9;int t=a[i];for(int j=2;j*j<=t;j++){if(t%j==0){if(!mp[j]) mp[j]=i;else pos=min(pos,mp[j]);while(t%j==0) t/=j;}}if(t>1){if(!mp[t]) mp[t]=i;else pos=min(pos,mp[t]);}return pos;
}
signed main(){int n;cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}int x=1e9,y=1e9;for(int i=1;i<=n;i++){int pos=get(i);if(pos!=1e9){if(pos<x||pos==x&&i<y){x=pos,y=i;}}}cout<<x<<' '<<y<<endl;return 0;
}子树的大小
题目描述
给定一棵包含 n 个结点的完全 m 叉树,结点按从根到叶、从左到右的顺序依次编号。
例如下图是一个拥有 11 个结点的完全 3 叉树。
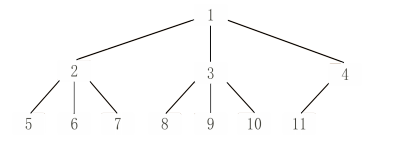
你需要求出第 k 个结点对应的子树拥有的结点数量。
输入格式
输入包含多组询问。
输入的第一行包含一个整数 T ,表示询问次数。
接下来 T 行,每行包含三个整数 n, m, k 表示一组询问。
输出格式
输出 T 行,每行包含一个整数表示对应询问的答案。
样例输入
3 1 2 1 11 3 4 74 5 3
样例输出
1 2 24
提示
对于 40% 的评测用例,T ≤ 50,n ≤ 10^6,m ≤ 16 ;
对于所有评测用例,1 ≤ T ≤ 10^5,1 ≤ k ≤ n ≤ 10^9,2 ≤ m ≤ 10^9 。
#include<iostream>
#include<vector>
#include<map>
#define int long long
using namespace std;
const int N=1e5+10;
int a[N];
signed main(){int T;scanf("%lld",&T);while(T--){int n,m,k;scanf("%lld%lld%lld",&n,&m,&k);bool flag=1;int cnt=1;int l=k,r=k;while(flag){//迭代计算k节点的子节点个数l=(l-1)*m+2;//最左边子节点的编号r=r*m+1;//最右边子节点的编号if(r>n){r=n;flag=0;}if(l<=n) cnt+=r-l+1;}printf("%lld\n",cnt);}return 0;
}这篇关于蓝桥杯第十四届C++C组的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







