本文主要是介绍MPT - 初识账户状态树(World State),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
往期回顾
- ETH网络中的账户
- ETH网络中的区块链
通过以上文章,我们了解到ETH网络中的
World State是节点根据交易维护的,节点在维护Wrold State时为了方便操作会将用户状态构建成一颗树,称为账户状态树,采用一种叫做MPT的数据结构
MPT
Merkle Patricia Tree(MPT)是一种数据结构,被广泛应用于以太坊中用于存储账户状态和交易数据。它结合了Merkle树和Patricia树的优点,既能够提供快速的数据验证和访问,又能够有效地利用存储空间
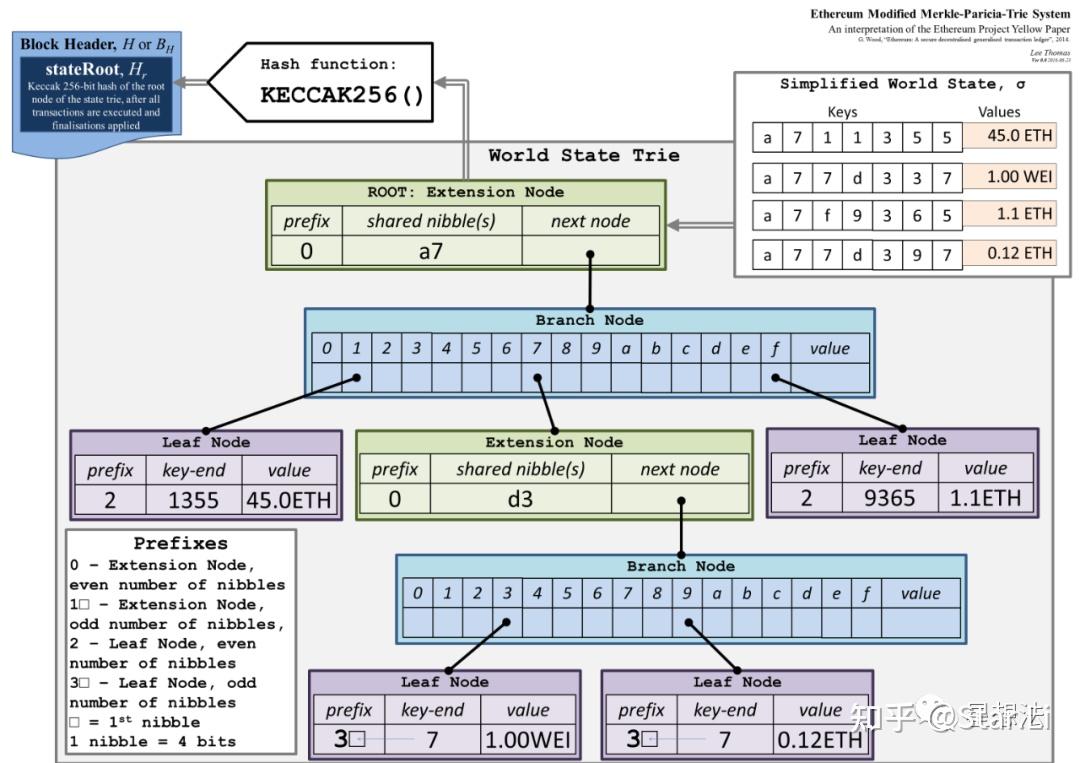
注:此图来自网络,如有侵权,联系删除
叶子节点存储了账户的信息。如果是合约账户,则会包含StorageRoot(合约状态数据的哈希值,可更新)和CodeHash(合约代码的哈希值,不可更改)
节点在提议区块时,区块头中必须包含账户状态树的RootHash
Block 19601313
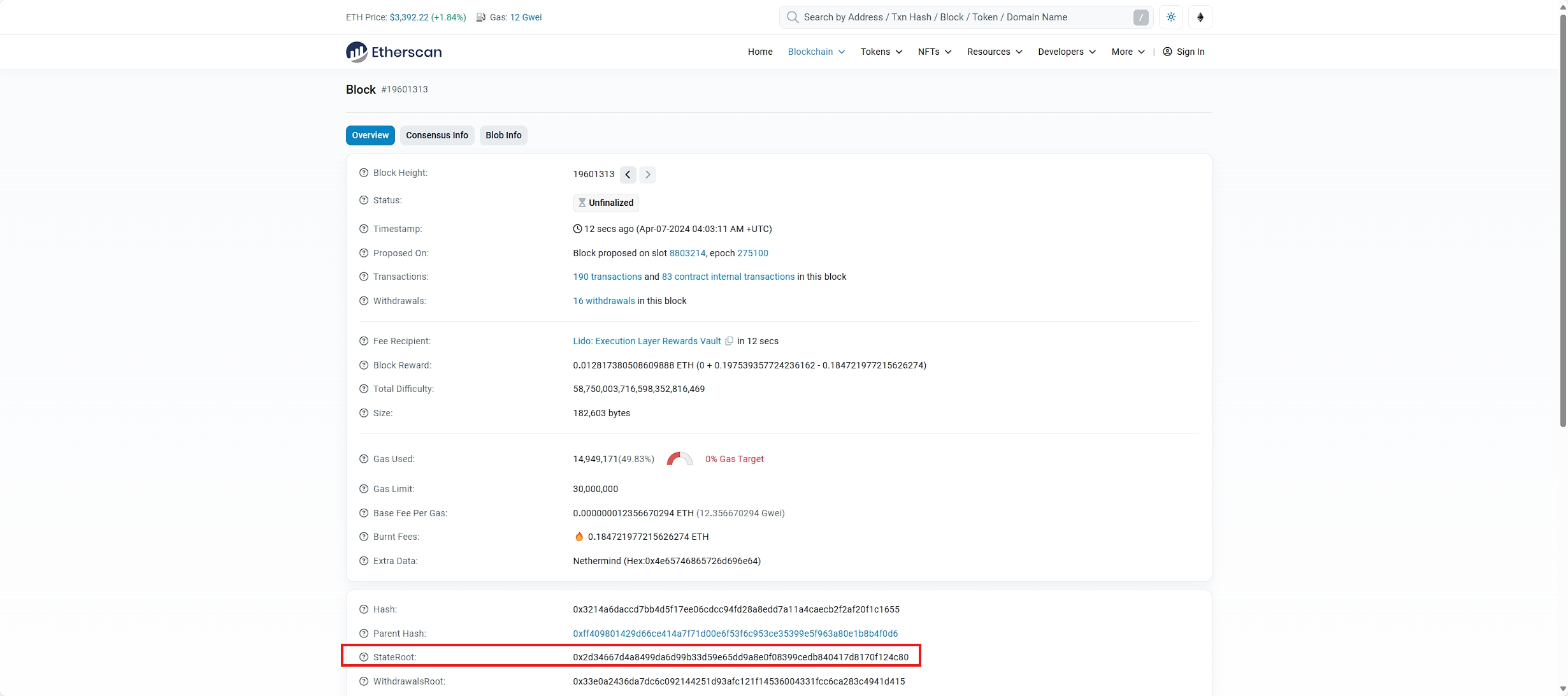
MPT的优点
MPT树具有以下几个关键特点:
-
哈希链接: 每个节点都包含一个哈希值,用于
验证节点的内容是否被篡改。通过哈希链接,可以快速验证整个树的完整性。 -
部分键匹配: MPT树使用前缀树的部分键匹配来
优化存储空间。只有节点的键的一部分被存储在该节点中,而不是整个键。这样可以大大减少存储空间的使用量。 -
可扩展性: MPT树具有良好的可扩展性,可以处理大量的数据。根据需求,可以
动态地添加或删除节点,而不会影响整个树的结构。 -
快速访问: MPT树支持
快速的数据访问。通过节点的哈希值,可以快速定位和检索存储在树中的数据,而无需遍历整个树。
文章预告
- Merkle树以及代码实现
- Patricia树以及代码实现
- 深入了解MPT运作方式
- 使用Python实现MPT
关注我,一起进入Web3的世界
这篇关于MPT - 初识账户状态树(World State)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






