本文主要是介绍WCH恒沁单片机-CH32V307学习记录2----FreeRTOS移植,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
RISC-V 单片机 FreeRTOS 移植
前面用了 5 篇博客详细介绍了 FreeRTOS 在 ARM Cortex-M3 MCU 上是如何运行的。
FreeRTOS从代码层面进行原理分析系列
现在我直接用之前的 RISC-V MCU 开发板子(CH32V307VCT6)再次对 FreeRTOS 进行移植,其实也不能说是从头到尾的移植,因为在官方的软件包中已经包含了对 FreeRTOS 移植的例子,但是这个软件包中很多通用的文件都是公用的,这样我们在实际使用的时候就不容易把某一个部分的功能处理的拉出来作为单独项目,这篇博客我就是打算帮助大家更快的解决这个问题。
将官方软件包中的例子抽出FreeRTOS部分
CH32软件包
官方软件包下载位置
在官方软件包中有这么一个文件叫做 CH32V30x_List.txt 这个里面就是软件包中各个文件夹中的内容的介绍。

这里,我的 CH32 库是目前(截至24年4月6日)最新的 2.4 版本。这里我使用的 IDE 是 MounRiver Studio,这个 IDE 也可以直接从官网获取。
MounRiver Studio 官网下载
对于 MounRiver Studio 的安装网上有很多,大家可以去网上找找,而且这并不是本篇的重点。
建立单独的项目文件夹
- 建立 FreeRTOS 文件夹,这里直接把 EVT 中也就是官方软件包中的 FreeRTOS 文件夹直接复制到,我们的想要的工程路径中。
- 在 FreeRTOS 中建立 SRC 目录,将 EVT\EXAM\SRC 文件夹中的 Core 和 Debug 目录也拷贝到 FreeRTOS 中的 SRC 中。

- 在 FreeRTOS 中建立 Driver 目录,将 EVT\EXAM\SRC\Peripheral 文件夹拷贝到 Driver 目录中。
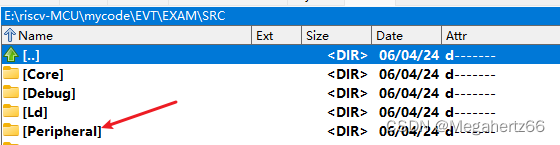
- 在原本的 FreeRTOS_Core\Startup 中原本有两个 汇编 文件,这里我们把 D8 删掉,只保留 D8C 就可以,因为这个是匹配我们 CH32V307 MCU 的。
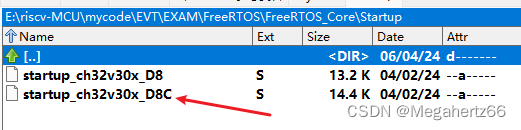
简单配置 MounRiver Studio
经过上面的步骤我们已经把文件分门别类的放到文件夹中了,接下来配置一下 MounRiver Studio 让它能找到我们新加的文件。
右键项目,选择属性选项。
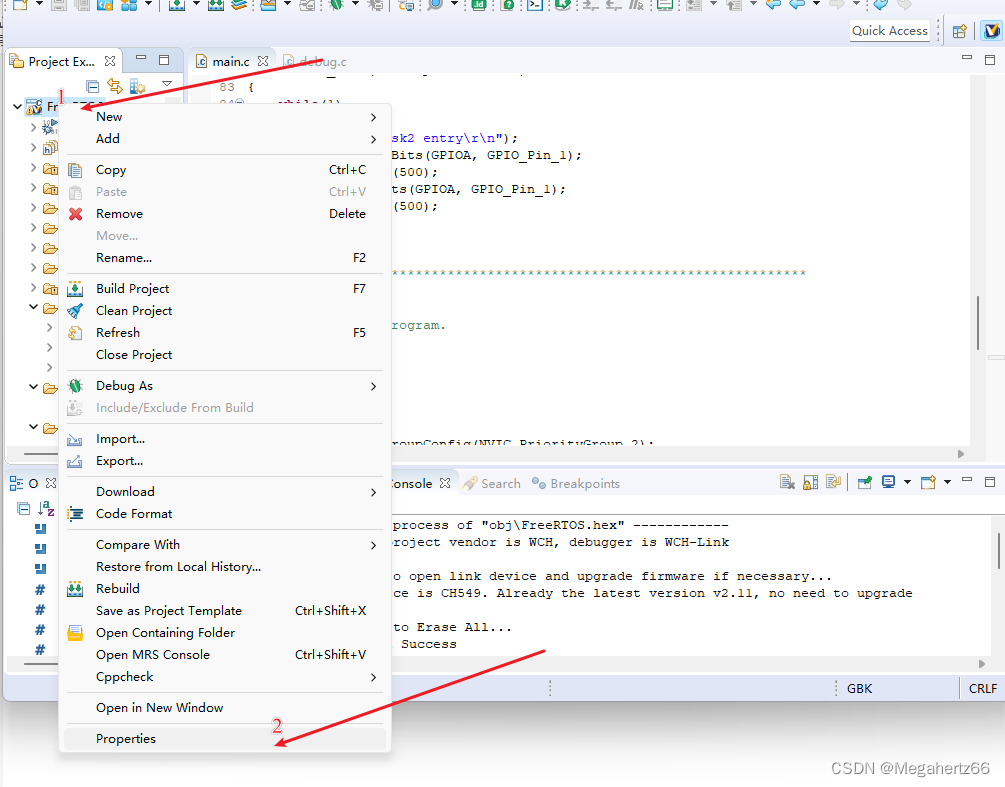
把本来出现在这里面的都删掉,我图片里面的删掉后自己自动生成的,这个不要再删除了。
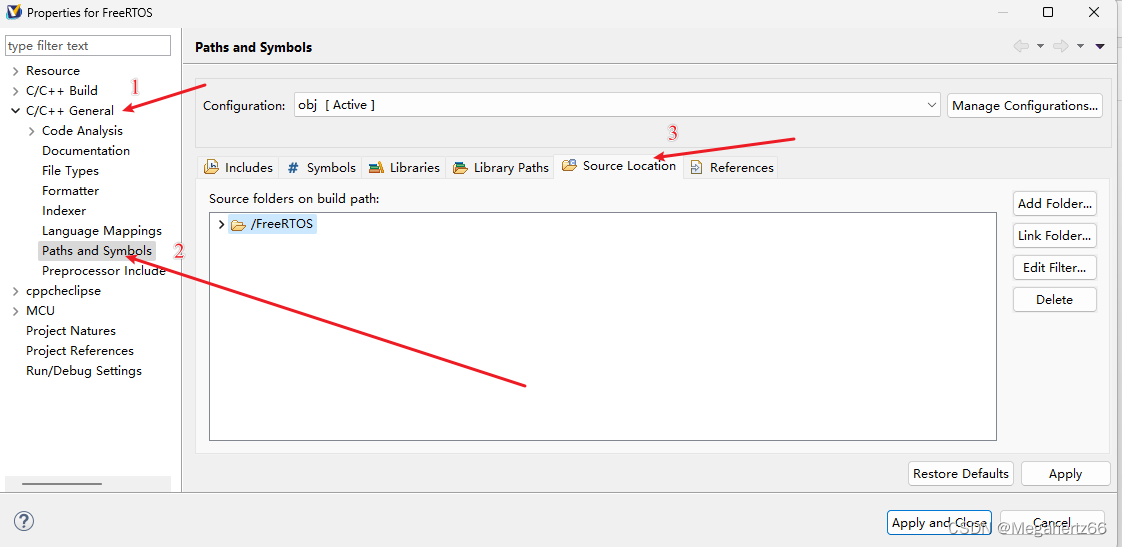
刷新一下项目。
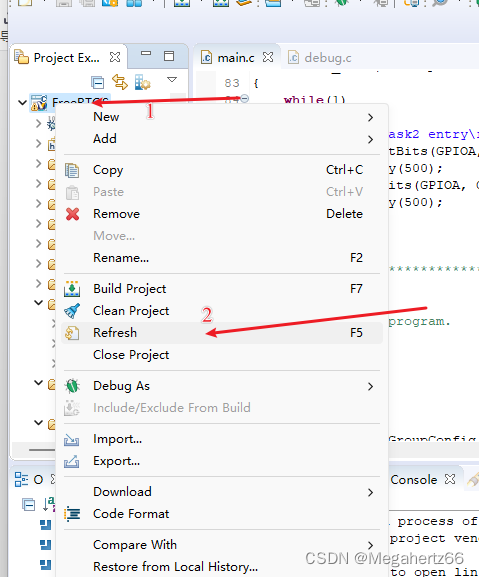
通过下面五步把咱们新加进去的文件告诉编译器,图片里面的不一定非常适合你的实际情况,你要根据的项目的路径进行填写。填的时候尽量像项目自带的几行一样,使用通配符的形式。 万一这里遇到报错也不要怕,一般都是没有找到文件,把 Error log 中提示找不到的文件全部添加以下就 ok 了。
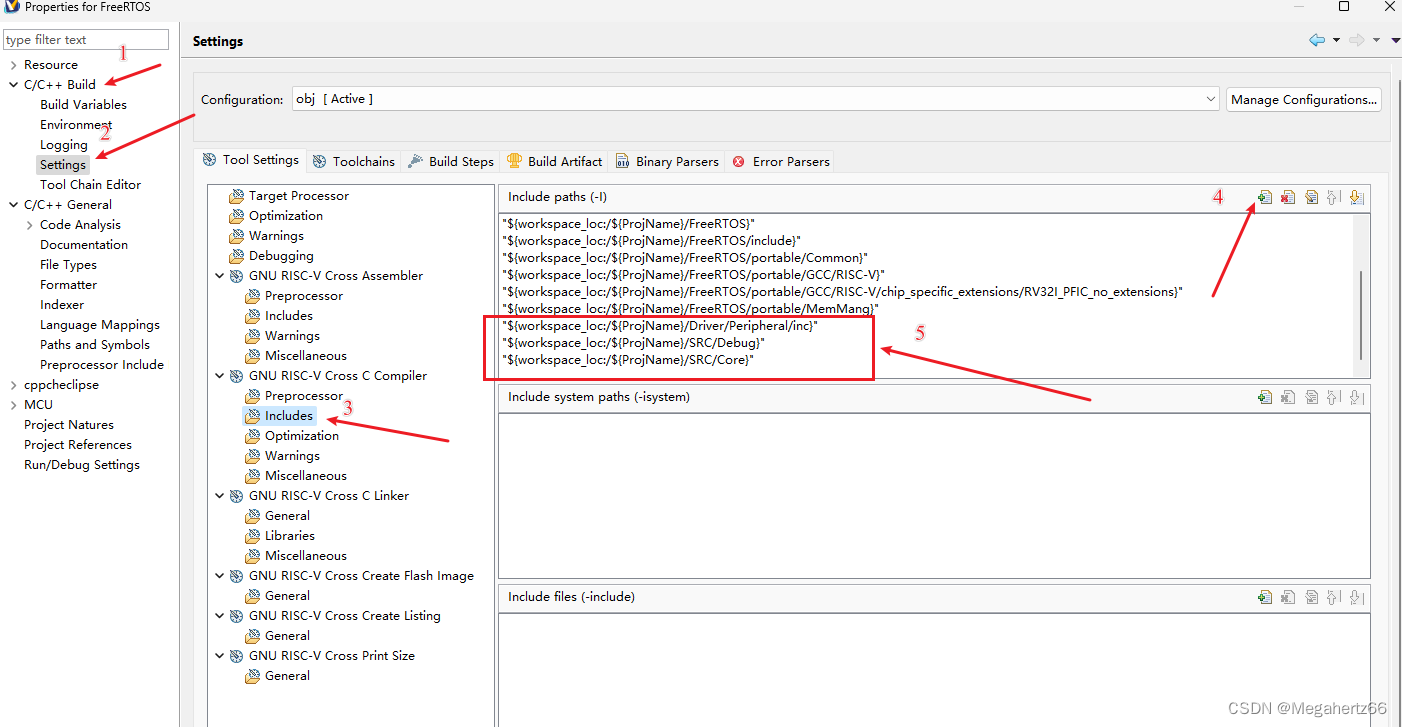
现在让我们编译一下,看看有没有错误。

非常简单就搞定了~ 因为我们懂得了 FreeRTOS 的原理,在不同平台上移植都是很轻松的事情,在这里再次推荐大家看看之前关于 FreeRTOS 的五篇博客,已经会让你对 FreeRTOS 有一个原理上的认识,以后用起来都会特别的方便。
前五篇博客的 Link
现象确认
至此,我们利用官方的软件包已经非常轻松的把 FreeRTOS 的部分单独抽取出来作为一个新的项目并且编译成功了。
现在让我们看看官方软件包中例子都做了些什么事情,可以让我们可以很直观的看到 FreeRTOS 的运行时的情况。
在代码中,建立了两个任务去打印字符串和开关一个 GPIO,这个 GPIO 应该是控制灯的。这里我们先不管,直接从串口看字符串,这样更加直观。
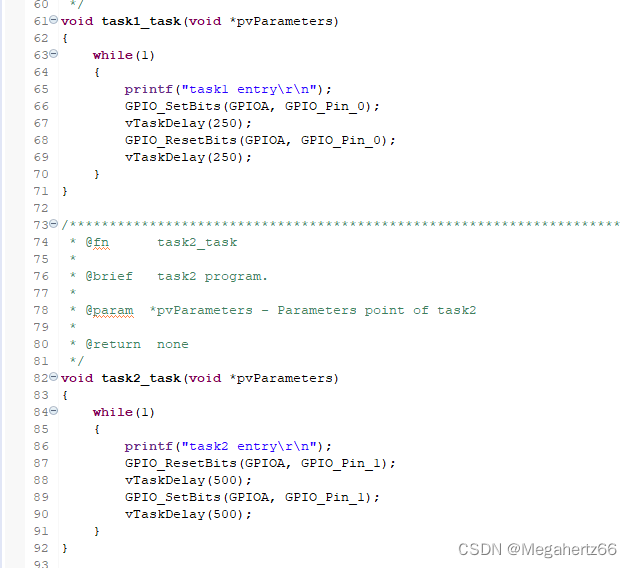
在 main 函数中,有个叫做 USART_Printf_Init 的函数,这个从名字看就是知道是配置 printf 从串口进行输出的。
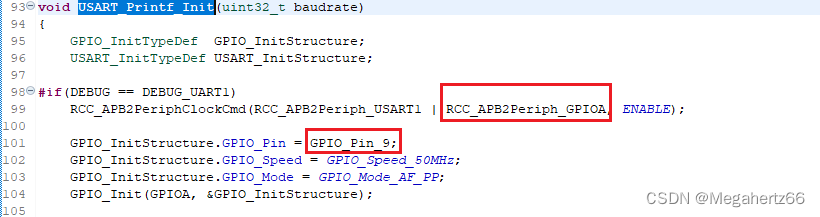
上面的代码看着很明显,是从 GPIOA 里面的 Pin 9 进行输出。让我们直接把串口的 RX 街道 PA9 上。

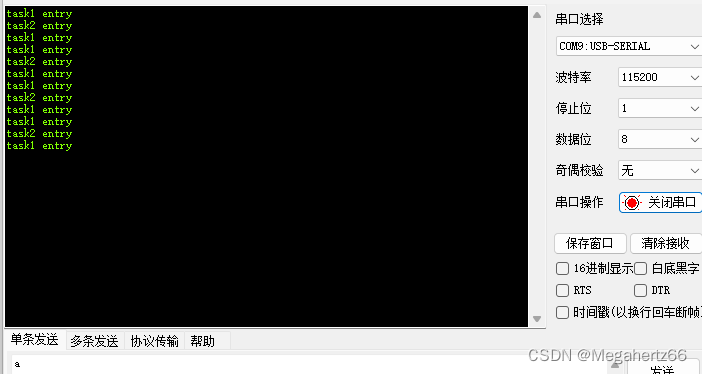
向板子上,下载一下我们刚才编译好的代码~ 从串口中的输出可以知道,我们的 FreeRTOS 已经跑起来了!

这篇关于WCH恒沁单片机-CH32V307学习记录2----FreeRTOS移植的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







