Codeforces 1631 E. Paint the Middle —— 贪心，一点点思维

本文主要是介绍Codeforces 1631 E. Paint the Middle —— 贪心，一点点思维，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

This way

题意：

给你长度为n的数组a，你每次可以选下标为i,j,k(i<j<k)的三个位置，并且a[i]=a[k]，然后销毁中间那个数，问你最多能销毁多少个数。

题解：

难度不高，我做的时候还没有评级，感觉应该不会超过23.和做前面题目用的时间差不多，果然应该去刷刷水题了。

做完之后看别人的代码发现好像有很短的？等写完这篇博客去研究研究。
一题多解的能力是非常必要的

首先能想到的是，任何一个数字最多只包括一个区间，假设:12315671，那么中间这个1是有必要的吗？显然没有。那么将每种出现两个及以上的数字作为左右端点来画包含的区间，可能是这样一幅图：
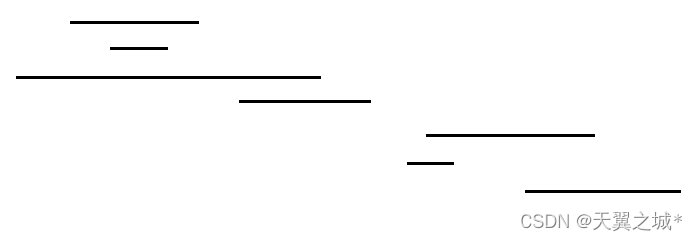
在这里插入图片描述
杂乱无章，似乎找不到突破口。
我此时看到这幅图的第一想法是：如果一个区间被另一个区间包括，那么它有必要存在吗？
例如：12345371
中间的这两个3能直接销毁，没有存在的必要。
于是我们可以将被包含的区间删掉，然后如果将其从左端点从小到大排序，会变成这样一幅图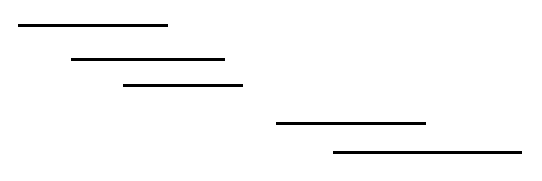：在这里插入图片描述
此时出现了一种我一开始没想到，后来wa了之后才想到的情况：
看上面第二条线，它有存在的必要吗？
例如：123123
那么2似乎没有存在的必要，因为1和3已经将2所能够包括的区间全都算到了。
于是需要将这种区间也销掉，我的做法是：确定第一条线，因为它的左端点没有任何人能够包括，所以它一定存在，然后将所有左端点在其之内的区间，找到一条右端点最右边的区间，其它全都不要。
然后依次做下去。

那最后怎么算？
通过几个例子找到了规律：
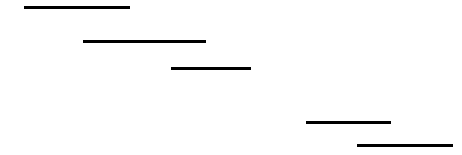
在这里插入图片描述
像上面这张图，前三个区间是联通的，和后两个区间是分离的，相互分离的区间完全可以分开考虑。于是我们考虑每一个连通块：假设这个连通块是由x条区间组成，那么其中的部分我们要尽量销掉最多，是否需要一条区间的左右端点在最终是存在的，并且其它区间的某一个端点是要被销毁的？幸好不用确定顺序，要不然还得动脑子
例如：1 9 2 1 10 8 3 2 5 4 3
我们可以留下一个1，一个2，两个3,。或者一些其它的情况，但是会发现，区间的左右端点一定会剩下一个，并且一定会有某个区间的左右端点会同时存在。当然你可以杠：我可以留下1,1，3,3把2给全部销毁呀！
你说得对，但是我们只需要找到一种通用的解法即可。如果这个连通块中有x个区间，那么你至少要留下x+1个端点。
我是使用类似差分的方法来做的，也就是最后一个for循环

#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
struct node{int l,r;bool operator< (const node& a)const {if(l==a.l)return r>a.r;return l<a.l;}
}a[N];
int sta[N],b[N],en[N];
int main()
{int n,x,tot=0;scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&x);if(sta[x])a[++tot]={sta[x],i};//找到每个区间elsesta[x]=i;}sort(a+1,a+1+tot);int all=1,r=a[1].r,p=2;en[a[1].r]=1;for(int i=2;i<=tot;i=p){//销毁不用的区间if(a[i].r<=r){p=i+1;continue;}r=a[i].r;a[++all]=a[i];p=i+1;while(p<=tot && a[p].l<=a[all-1].r){//对于每一个区间找到左端点在它内且右端点最大if(r<=a[p].r)a[all]=a[p],r=a[p].r;p++;}en[a[all].r]++;}int now=1,ans=0,sum=0,len=0,mx=0;/*now:现在到了第几个区间ans:最终答案sum:现在在几个区间中mx:当前连通块有多少个区间len:当前连通块的长度*/for(int i=a[1].l;i<=n;i++){while(now<=all && a[now].l<i)now++;while(now<=all && a[now].l==i)now++,sum++,mx++;if(sum)len++;sum-=en[i];if(!sum)ans+=max(0,len-mx-1),len=0,mx=0;}printf("%d\n",ans);return 0;
}