骑士

2024-04-06 09:58
文章标签 骑士

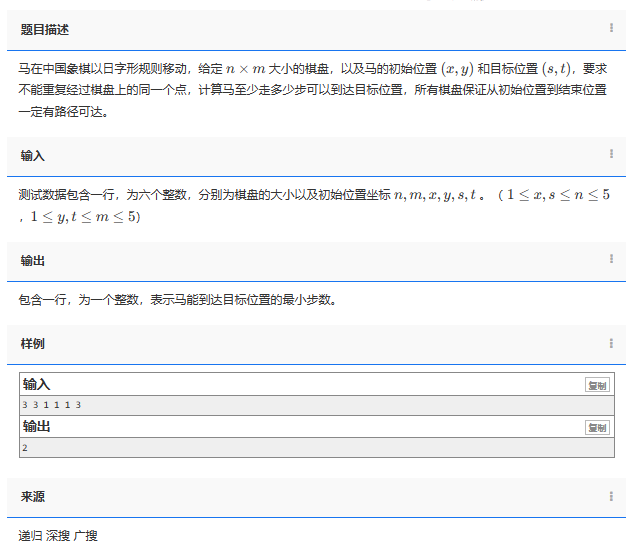
本文主要是介绍骑士，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Code:
  1. #include <stdio.h>    
  2. int board[8][8] = {0};   
  3.   
  4. int travel(int x, int y) ;   
  5.     
  6. int main(void)    
  7. {       
  8.     int startx, starty;       
  9.     int i, j;       
  10.     printf("輸入起始點：");       
  11.     scanf("%d %d", &startx, &starty);       
  12.     if(travel(startx, starty))    
  13.     {           
  14.         printf("遊歷完成！/n");       
  15.     }       
  16.     else    
  17.     {           
  18.         printf("遊歷失敗！/n");       
  19.     }       
  20.     for(i = 0; i < 8; i++)    
  21.     {           
  22.         for(j = 0; j < 8; j++)    
  23.         {               
  24.             printf("%2d ", board[i][j]);           
  25.         }           
  26.         putchar('/n');   
  27.     }   
  28.         
  29.     return 0;   
  30.  }    
  31.  int travel(int x, int y)    
  32.  {       
  33.     // 對應騎士可走的八個方向       
  34.      int ktmove1[8] = {-2, -1, 1, 2, 2, 1, -1, -2};       
  35.      int ktmove2[8] = {1, 2, 2, 1, -1, -2, -2, -1};       
  36.      // 測試下一步的出路       
  37.      int nexti[8] = {0};       
  38.      int nextj[8] = {0};       
  39.      // 記錄出路的個數       
  40.      int exists[8] = {0};       
  41.      int i, j, k, m, l;       
  42.      int tmpi, tmpj;       
  43.      int count, min, tmp;       
  44.      i = x;       
  45.      j = y;       
  46.      board[i][j] = 1;       
  47.      for(m = 2; m <= 64; m++)    
  48.      {           
  49.         for(l = 0; l < 8; l++)    
  50.         {               
  51.             exists[l] = 0;           
  52.         }           
  53.         l = 0;           
  54.         // 試探八個方向           
  55.         for(k = 0; k < 8; k++)   
  56.         {               
  57.             tmpi = i + ktmove1[k];               
  58.             tmpj = j + ktmove2[k];              
  59.              // 如果是邊界了，不可走               
  60.              if(tmpi < 0 || tmpj < 0 || tmpi > 7 || tmpj > 7)                   
  61.                 continue;               
  62.              // 如果這個方向可走，記錄下來               
  63.              if(board[tmpi][tmpj] == 0)    
  64.              {                   
  65.                 nexti[l] = tmpi;                   
  66.                 nextj[l] = tmpj;                   
  67.                 // 可走的方向加一個                   
  68.                  l++;              
  69.              }           
  70.          }           
  71.          count = l;           
  72.          // 如果可走的方向為0個，返回           
  73.          if(count == 0)    
  74.          {               
  75.             return 0;           
  76.          }           
  77.          else if(count == 1)    
  78.          {               
  79.             // 只有一個可走的方向               
  80.              // 所以直接是最少出路的方向              
  81.               min = 0;           
  82.          }          
  83.          else    
  84.          {              
  85.             // 找出下一個位置的出路數               
  86.                for(l = 0; l < count; l++)    
  87.                {                   
  88.                     for(k = 0; k < 8; k++)    
  89.                     {                       
  90.                        tmpi = nexti[l] + ktmove1[k];                       
  91.                        tmpj = nextj[l] + ktmove2[k];                       
  92.                        if(tmpi < 0 || tmpj < 0 || tmpi > 7 || tmpj > 7)    
  93.                        {                           
  94.                           continue;                       
  95.                        }                       
  96.                        if(board[tmpi][tmpj] == 0)                           
  97.                                 exists[l]++;                   
  98.                      }               
  99.                  }               
  100.                  tmp = exists[0];               
  101.                  min = 0;               
  102.                  // 從可走的方向中尋找最少出路的方向               
  103.                  for(l = 1; l < count; l++)    
  104.                  {                   
  105.                     if(exists[l] < tmp)    
  106.                      {                       
  107.                         tmp = exists[l];                       
  108.                         min = l;                   
  109.                      }               
  110.                  }           
  111.              }           
  112.              // 走最少出路的方向           
  113.              i = nexti[min];           
  114.              j = nextj[min];           
  115.              board[i][j] = m;       
  116.      }       
  117.      return 1;   
  118.  }    

 

这篇关于骑士的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/879629。

相关文章

Day 27：2596. 检查骑士巡视方案

Day 27：2596. 检查骑士巡视方案

Leetcode 2596. 检查骑士巡视方案 骑士在一张 n x n 的棋盘上巡视。在 **有效 **的巡视方案中，骑士会从棋盘的 左上角 出发，并且访问棋盘上的每个格子 恰好一次 。 给你一个 n x n 的整数矩阵 grid ，由范围 [0, n * n - 1] 内的不同整数组成，其中 grid[row][col] 表示单元格 (row, col) 是骑士访问的第 grid[row][
阅读更多...
【C++题解】1438 - 骑士巡游

【C++题解】1438 - 骑士巡游

问题：1438 - 骑士巡游 类型：递归 深搜 广搜 题目描述： 马在中国象棋以日字形规则移动，给定 n×m 大小的棋盘，以及马的初始位置 (x,y) 和目标位置 (s,t)，要求不能重复经过棋盘上的同一个点，计算马至少走多少步可以到达目标位置，所有棋盘保证从初始位置到结束位置一定有路径可达。 输入： 测试数据包含一行，为六个整数，分别为棋盘的大小以及初始位置坐标 n,m,x,y,s
阅读更多...
记录一下自己的宏碁暗影骑士电脑的属性

记录一下自己的宏碁暗影骑士电脑的属性

@TOC 前言 没有前言。 参考博文 怎么查自己电脑服务器信息吗,如何查看自己电脑的服务器 一、cmd 看到服务器型号 wmic csproduct get name 查询CPU个数 按照博主的方法，我出现了报错。 在 Windows 上，您可以通过 PowerShell 来执行类似的操作。您可以打开 PowerShell 并输入以下命令： (Get-WmiObje
阅读更多...
BZOJ1085. [SCOI2005]骑士精神（IDA*算法）

BZOJ1085. [SCOI2005]骑士精神（IDA*算法）

Description 　　在一个5×5的棋盘上有12个白色的骑士和12个黑色的骑士， 且有一个空位。在任何时候一个骑士都能按照骑 士的走法（它可以走到和它横坐标相差为1，纵坐标相差为2或者横坐标相差为2，纵坐标相差为1的格子）移动到空 位上。 给定一个初始的棋盘，怎样才能经过移动变成如下目标棋盘： 为了体现出骑士精神，他们必须以最少的步 数完成任务。 Input 　　第一行有一个正整数T(T<
阅读更多...
蓝桥杯算法题：蓝桥骑士

蓝桥杯算法题：蓝桥骑士

题目描述 小明是蓝桥王国的骑士，他喜欢不断突破自我。 这天蓝桥国王给他安排了 N 个对手，他们的战力值分别为 a_1,a_2,…,a_n，且按顺序阻挡在小明的前方。对于这些对手小明可以选择挑战，也可以选择避战。 身为高傲的骑士，小明从不走回头路，且只愿意挑战战力值越来越高的对手。 请你算算小明最多会挑战多少名对手。 输入描述 输入第一行包含一个整数 N，表示对手的个数。 第二行包含 N 个整数
阅读更多...
【线性规划与网络流24题#24】骑士共存

【线性规划与网络流24题#24】骑士共存

问题描述 在一个n×n个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入。 对于给定的n*n个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击。 输入格式 第一行有2 个正整数n 和m (1<=n<=200, 0<=m<n2)， 分别表示棋盘的大小和障碍数。接下来的m 行给出障碍的位置。每行2 个正整数，表示
阅读更多...
《程序员》算法擂台之骑士聚会问题（c语言版）　一

《程序员》算法擂台之骑士聚会问题（c语言版）　一

#include  < stdio.h > #include  < stdlib.h > #include < time.h > struct  point {      int  x;      int  y;      int *  CastStep; }; point *  GetCanGo(point, int ); void  Walk(point, int ); int
阅读更多...
Acer宏碁暗影骑士擎AN515-58笔记本电脑工厂模式原厂Win11系统ISO镜像安装包下载

Acer宏碁暗影骑士擎AN515-58笔记本电脑工厂模式原厂Win11系统ISO镜像安装包下载

宏基AN515-58原装出厂OEM预装Windows11系统工厂包，恢复出厂时开箱状态一模一样，带恢复还原功能 链接：https://pan.baidu.com/s/1iCVSYtList-hPqbyTyaRqQ?pwd=t2gw  提取码：t2gw 宏基原装系统自带所有驱动、NITROSENSE风扇键盘灯控制中心、Office办公软件、出厂主题壁纸、系统属性联机支持标志、  Acer Ca
阅读更多...
深入理解“骑士”漏洞 VoltJockey

深入理解“骑士”漏洞 VoltJockey

先理解一下题目：VoltJockey: Breaching TrustZone by Software-Controlled Voltage Manipulation over Multi-core Frequencies，这个漏洞打破了ARM下的TrustZone（可信执行环境），通过使用软件控制的电压来影响多核上的频率来达到目的，这个软件实际上就是DVFS（dynamic voltage a
阅读更多...
688. 骑士在棋盘上的概率

688. 骑士在棋盘上的概率

Problem: 688. 骑士在棋盘上的概率 文章目录 思路解题方法复杂度Code 思路 这是一个动态规划问题。我们需要计算骑士在棋盘上移动k次后仍然留在棋盘上的概率。骑士的每一步都有8种可能的移动方式，因此我们可以使用一个三维数组dp[i][j][k]来存储骑士在第k步时位于棋盘的(i, j)位置的概率。 解题方法 初始化一个三维数组dp，其中dp[i][
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2