【面试HOT200】数组篇

本文主要是介绍【面试HOT200】数组篇，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

系列综述：
💞目的：本系列是个人整理为了秋招面试coding部分的，整理期间苛求每个算法题目，平衡可读性与代码性能（leetcode运行复杂度均打败80%以上）。
🥰来源：材料主要源于【CodeTopHot200】进行的，每个知识点的修正和深入主要参考各平台大佬的文章，其中也可能含有少量的个人实验自证，所有代码均优先参考最佳性能。
🤭结语：如果有帮到你的地方，就点个赞和关注一下呗，谢谢🎈🎄🌷！！！
🌈【C++】秋招&实习面经汇总篇

---

---

😊点此到文末惊喜↩︎

基础题目

二分查找

基础知识

1. 适应场景：有序无重复的数组
   • 有序：一次比较即可确定需要查找的另一半，效率高的关键
   • 无重复：一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一，需要进行左右的循环查找
   • 数组：可以进行随机存取
2. 细节
   • 快速防溢出的除2：mid = L + ((R - L)>>1)
     • 防溢出：如果L 和 R太大，直接相加就有溢出的可能
     • 右移：等价于除法算法，但是效率高
   • 使用前闭后闭的二分区域查找，可以在查找target位置后再进行相同元素相连区域的定位操作。
3. leetcode题目：704. 二分查找

   // *****************前闭后闭的基本二分查找，可以代替下一种*******************
   int search(vector<int>& nums, int target) {
   // 0. 健壮性检查if(nums.size() <= 0) return -1;
   // 1. 定义边界指针（指向遍历数组区域的边界位置）int left = 0;int right = nums.size() - 1; // 定义target在左闭右闭的区间里
   // 2. 基本算法步骤的循环    while (left <= right) { // 前闭后闭用<=// 划分中间int mid = left + ((right - left)>>1);	// 防止溢出 等同于(left + right)/2if (target < nums[mid]) {				// 目标值在左区间right = mid - 1; } else if (target > nums[mid]) {		// 目标值在右区间left = mid + 1; } else {								// 找到目标值，即相等时return mid; 						// 数组中找到目标值，直接返回下标}}
   // 3. 添加进行左右边界的定位操作// ...return left;// left为相等值未找到时应插入的位置，也可使用-1表示
   }
   

相关例题

1. leetcode题目：35. 在排序数组中查找元素的第一个和最后一个位置
   • 先通过基本二分法查找目标元素出现的位置
   • 然后使用while(边界判断 && 值判断)获得target值的区间

   ···	// 基本二分查找
   // 寻找相似相邻区间的左右边界
   int l = mid;
   int r = mid;
   if(nums[mid] != target){return res;
   }else{while (vec[left] == target && left >= 0) {--left;}while (vec[right] == target && right <= vec.size() - 1) {++right;}
   }
   res[0]=l;
   res[1]=r;
   return res;
   }
   

2. 33. 搜索旋转排序数组
   • 整数数组 nums 按升序排列，但是可以进行循环移位，然后进行target的查找
   • 使用时间复杂度为 O(log n) 的算法
     
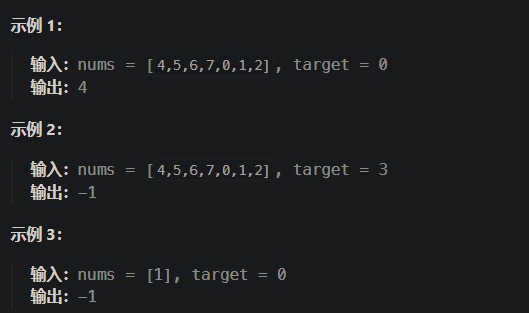
   • 思路
     • nums[0] <= nums[mid]（0 - mid不包含旋转）且nums[0] <= target <= nums[mid] 时 high 向前规约；
     • nums[mid] < nums[0]（0 - mid包含旋转），target <= nums[mid] < nums[0] 时向前规约（target 在旋转位置到 mid 之间）
     • nums[mid] < nums[0]，nums[mid] < nums[0] <= target 时向前规约（target 在 0 到旋转位置之间）
     • 其他情况向后规约
     • nums[mid] < nums[0]，nums[0] > target，target > nums[mid] 三项均为真或者只有一项为真时向后规约

int search(vector<int>& nums, int target) {int lo = 0, hi = nums.size() - 1;while (lo < hi) {int mid = (lo + hi) / 2;if ((nums[0] > target) ^ (nums[0] > nums[mid]) ^ (target > nums[mid]))lo = mid + 1;elsehi = mid;}return lo == hi && nums[lo] == target ? lo : -1;
}

3. 正序数组查找第k小（二分查找）
   • 给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数
   • 算法的时间复杂度应该为 O(log (m+n))

class Solution {
public:int findKthElm(vector<int>& nums1,vector<int>& nums2,int k){assert(1<=k&&k<=nums1.size()+nums2.size());int le=max(0,int(k-nums2.size())),ri=min(k,int(nums1.size()));while(le<ri){int m=le+(ri-le)/2;if(nums2[k-m-1]>nums1[m]) le=m+1;//这为什么只写一个条件？！因为这是二分的排除条件，不是目标的符合条件，相当于排除条件，最后的结果才是符合条件的结果else ri=m;}//循环结束时的位置le即为所求位置，第k小即为max(nums1[le-1]),nums2[k-le-1])，但是由于le可以为0、k,所以//le-1或者k-le-1可能不存在所以下面单独判断下int nums1LeftMax=le==0?INT_MIN:nums1[le-1];int nums2LeftMax=le==k?INT_MIN:nums2[k-le-1];return max(nums1LeftMax,nums2LeftMax);}double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {int n=nums1.size()+nums2.size();if(n&1){//两个数组长度和为奇数return findKthElm(nums1,nums2,(n>>1)+1);}else{//为偶数return (findKthElm(nums1,nums2,n>>1)+findKthElm(nums1,nums2,(n>>1)+1))/2.0;}}
};

快速排序（模糊划分）

基础知识

1. 基本思想
   • 选择基准：在待排序列中，按照某种方式挑出一个元素，作为 “基准”（pivot）
   • 分割操作：以该基准在序列中的实际位置，把序列分成两个子序列。此时，在基准左边的元素都比该基准小，在基准右边的元素都比基准大
   • 递归地对两个序列进行快速排序，直到序列为空或者只有一个元素。
2. 特点
   • 不产生有序子序列，但每次排序后会将基准元素放到最终位置上
   • 每次排序划分子区间越相近越能发挥快排优势
   • 每次可将无序线性表划分成小值区、pivot和大值区
3. 算法

int partition(vector<int> &vec, int left, int right) {// 将第一个元素随机化，避免有序数组导致的划分失衡int idx = left + rand() % (right - left + 1);swap(vec[left], vec[idx]);// 初始化：划分元素的位置和值int pos = left;int pivot = vec[left];// 算法部分while (left < right) {// 从后向前找 小于 基准元素的while (vec[right] >= pivot && left < right) --right;// 从前向后找 大于 基准元素的while (vec[left] <= pivot && left < right) ++left;swap(vec[left], vec[right]);}swap(vec[left], vec[pos]);return left;	
}void QuickSort(vector<int> &vec, int left, int right) {if (left > right) return ;int pivot = partition(vec, left, right);QuickSort(vec, left, pivot-1);QuickSort(vec, pivot+1, right);
}

相关例题

1. 215. 数组中的第K个最大元素
   • 题目：给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。
   • 思路
     • 快排划分：时间复杂度：O(N) 空间复杂度：O(1)
     • 堆求解：时间复杂度：O(Nlog⁡K) 空间复杂度：O(K)

// 快排划分 
int findKthLargst(vector<int>& nums, int k) {// 划分函数(key：从大到小)auto partition = [&](int left, int right)->int{// 随机化：避免划分失败int idx = left + rand() % (right-left+1);swap(nums[left], nums[idx]);// 划分元素的位置和值int pos = left;int pivot = nums[left];while (left < right) {while (nums[right] <= pivot && left < right) --right;while (nums[left] >= pivot && left < right) ++left;swap(nums[left], nums[right]);}// 划分转移swap(nums[left], nums[pos]);return left;};// 算法int left = 0;int right = nums.size()-1;// 找到正序数组中的第k大while (left <= right) {int mid = partition(left, right);if (k == mid+1) {return nums[mid];} else if (k > mid+1) {left = mid+1;} else {right = mid-1;}}return 0;
}
// 堆处理
int findKthLargest(vector<int>& nums, int k) {priority_queue<int> pq;for (auto &i : nums) {pq.push(i);}for (int i = 0; i < k-1; ++i) {pq.pop();}return pq.top();
}

移除元素（快慢指针）

1. leetcode题目：27. 移除元素
   • 要求：使用快慢指针以O(n)的时间复杂度和O(1)的空间复杂度进行处理
   • 注意点
     • 快指针fast用于条件判断，慢指针slow用于位置保存
     • 尽量使用for循环避免结尾迭代条件的忘记

   int removeElement(vector<int>& nums, int val) {int slow = 0, fast = 0;     // 定义快慢指针for (; fast < nums.size(); ++fast) {// 快指针进行判断判断if (nums[fast] != val) {nums[slow] = nums[fast];++slow;}}nums.resize(slow);return slow;
   }
   

两数之和（带哈希缓存的查找）

1. leetcode1. 两数之和
2. 思路
   • 每次获取一个元素，先判断是否成功，如果不成功则将元素放入哈希缓存表中

   vector<int> twoSum(vector<int>& nums, int target) {vector<int> res;unordered_map<int, int> umap;for (int i = 0; i < nums.size(); ++i) {auto itr = umap.find(target-nums[i]);if (itr != umap.end()) {res.emplace_back(i);res.emplace_back(itr->second);}umap[nums[i]] = i;}return res;
   }
   

三数之和（排序+三指针）

1. 15. 三数之和
   • 给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。
   • 答案中不可以包含重复的三元组。
2. 思路
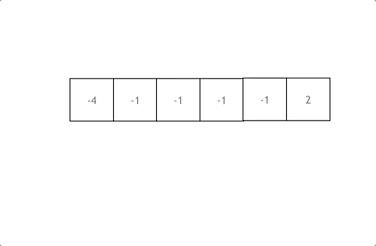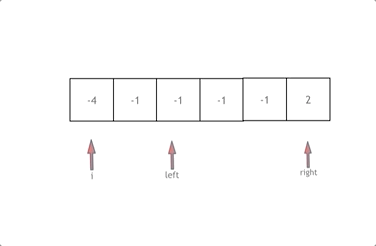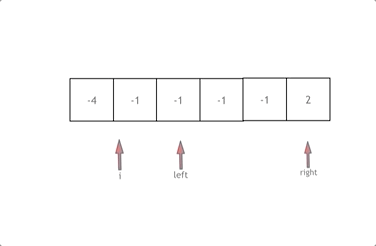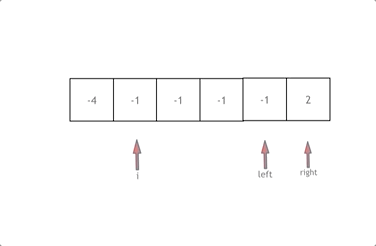
   • 固定一个指针进行问题的降维，然后另外两个指针进行区间的运算
     

vector<vector<int>> threeSum(vector<int>& nums) {const int len = nums.size();vector<vector<int>> res;sort(nums.begin(), nums.end());// 健壮性检查 if (nums.size() < 3 || nums[0] > 0 || nums[nums.size()-1] < 0)return res;// 算法部分// 找出a + b + c = 0// a = nums[i], b = nums[left], c = nums[right]for (int i = 0; i < nums.size(); i++) {// 排序后若第一个元素大于零，则表示后面元素不可能凑成三元组if (nums[i] > 0) return res;// 正确去重方法：比较i和i+1会遗漏掉第一个元素作为首元素的情况if (i > 0 && nums[i] == nums[i - 1]) continue;// 确定剩余两个元素的区间int left = i + 1;int right = nums.size() - 1;while (left < right) {if (nums[i] + nums[left] + nums[right] > 0) right--;else if (nums[i] + nums[left] + nums[right] < 0) left++;else {// 压入第一个，然后对后面的去重res.push_back(vector<int>{nums[i], nums[left], nums[right]});// 去重逻辑应该放在找到一个三元组之后，对b 和 c去重while (right > left && nums[right] == nums[right - 1]) right--;while (right > left && nums[left] == nums[left + 1]) left++;// 找到答案时，双指针同时收缩right--;left++;}}}return res;
}

3. 注意点
   • 去重操作
     • if (nums[i] == nums[i + 1]) continue;会导致[-1,-1,2]情况的遗漏
     • if (i > 0 && nums[i] == nums[i - 1]) continue;优先判断左部分，不会影响右部分

四数相加II（unordered_map的使用）

1. leetcode题目：四数相加
   • 记录去重和常数级查找通过unordered_set解决
     

   int fourSumCount(vector<int>& A, vector<int>& B, vector<int>& C, vector<int>& D) {unordered_map<int, int> umap; //key:a+b的数值，value:a+b数值出现的次数// 遍历大A和大B数组，统计两个数组元素之和，和出现的次数，放到map中for (int a : A) {for (int b : B) {umap[a + b]++;}}int count = 0; // 统计a+b+c+d = 0 出现的次数// 在遍历大C和大D数组，找到如果 0-(c+d) 在map中出现过的话// 就把map中key对应的value也就是出现次数统计出来。for (int c : C) {for (int d : D) {int val = -(c+d);if (umap.count(val) > 0) {count += umap[val];}}}return count;
   }
   

有序数组的平方（双端指针）

1. leetcode题目：977. 有序数组的平方
   
2. 思路：
   • 正常思路：从0开始向中间 + 辅助空间
   • 逆向思路：left和right两个指针分别从两端向中间进行夹逼

vector<int> sortedSquares(vector<int>& nums) {// 健壮性检查// 初始化const int len = nums.size();int left = 0;int right = len-1;vector<int> res(len);// 算法部分for (int index = len-1; left <= right; --index) {if (nums[left] * nums[left] > nums[right] *nums[right]) {res[index] = nums[left] * nums[left];++left;} else {res[index] = nums[right] *nums[right];--right;}}return res;
}

---

少年，我观你骨骼清奇，颖悟绝伦，必成人中龙凤。 不如点赞·收藏·关注一波

---

🚩点此跳转到首行↩︎

参考博客

1. 「代码随想录」
2. codetop前200
3. 力扣（LeetCode）
4. 旋转数组——极简 Solution

这篇关于【面试HOT200】数组篇的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---