LeetCode 每日一题 Day 116-122

本文主要是介绍LeetCode 每日一题 Day 116-122，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

2580. 统计将重叠区间合并成组的方案数

给你一个二维整数数组 ranges ，其中 ranges[i] = [starti, endi] 表示 starti 到 endi 之间（包括二者）的所有整数都包含在第 i 个区间中。

你需要将 ranges 分成两个组（可以为空），满足：

每个区间只属于一个组。
两个有交集的区间必须在同一个组内。
如果两个区间有至少一个公共整数，那么这两个区间是有交集的。

比方说，区间 [1, 3] 和 [2, 5] 有交集，因为 2 和 3 在两个区间中都被包含。
请你返回将 ranges 划分成两个组的总方案数。由于答案可能很大，将它对 109 + 7 取余后返回。

示例 1：

输入：ranges = [[6,10],[5,15]]
输出：2
解释：
两个区间有交集，所以它们必须在同一个组内。
所以有两种方案：

将两个区间都放在第 1 个组中。
将两个区间都放在第 2 个组中。
示例 2：

输入：ranges = [[1,3],[10,20],[2,5],[4,8]]
输出：4
解释：
区间 [1,3] 和 [2,5] 有交集，所以它们必须在同一个组中。
同理，区间 [2,5] 和 [4,8] 也有交集，所以它们也必须在同一个组中。
所以总共有 4 种分组方案：

所有区间都在第 1 组。
所有区间都在第 2 组。
区间 [1,3] ，[2,5] 和 [4,8] 在第 1 个组中，[10,20] 在第 2 个组中。
区间 [1,3] ，[2,5] 和 [4,8] 在第 2 个组中，[10,20] 在第 1 个组中。

提示：

1 <= ranges.length <= 1e5
ranges[i].length == 2
0 <= starti <= endi <= 1E9

合并区间，抄的灵神（菜：

class Solution {
public:int countWays(vector<vector<int>>& ranges) {ranges::sort(ranges, [](auto& a, auto& b) { return a[0] < b[0]; });int ans = 1, max_r = -1;for (auto& p : ranges) {if (p[0] > max_r) {                // 无法合并ans = ans * 2 % 1'000'000'007; // 新区间}max_r = max(max_r, p[1]); // 合并}return ans;}
};

1997. 访问完所有房间的第一天

你需要访问 n 个房间，房间从 0 到 n - 1 编号。同时，每一天都有一个日期编号，从 0 开始，依天数递增。你每天都会访问一个房间。

最开始的第 0 天，你访问 0 号房间。给你一个长度为 n 且下标从 0 开始的数组 nextVisit 。在接下来的几天中，你访问房间的次序将根据下面的规则决定：

假设某一天，你访问 i 号房间。
如果算上本次访问，访问 i 号房间的次数为奇数，那么第二天需要访问 nextVisit[i] 所指定的房间，其中 0 <= nextVisit[i] <= i 。
如果算上本次访问，访问 i 号房间的次数为偶数，那么第二天需要访问 (i + 1) mod n 号房间。
请返回你访问完所有房间的第一天的日期编号。题目数据保证总是存在这样的一天。由于答案可能很大，返回对 109 + 7 取余后的结果。

示例 1：

输入：nextVisit = [0,0]
输出：2
解释：

第 0 天，你访问房间 0 。访问 0 号房间的总次数为 1 ，次数为奇数。
下一天你需要访问房间的编号是 nextVisit[0] = 0
第 1 天，你访问房间 0 。访问 0 号房间的总次数为 2 ，次数为偶数。
下一天你需要访问房间的编号是 (0 + 1) mod 2 = 1
第 2 天，你访问房间 1 。这是你第一次完成访问所有房间的那天。
示例 2：

输入：nextVisit = [0,0,2]
输出：6
解释：
你每天访问房间的次序是 [0,0,1,0,0,1,2,…] 。
第 6 天是你访问完所有房间的第一天。
示例 3：

输入：nextVisit = [0,1,2,0]
输出：6
解释：
你每天访问房间的次序是 [0,0,1,1,2,2,3,…] 。
第 6 天是你访问完所有房间的第一天。

提示：

n == nextVisit.length
2 <= n <= 105
0 <= nextVisit[i] <= i

前缀和优化DP，开始思路是对的，后面wa了不会取模：

class Solution {
public:int firstDayBeenInAllRooms(vector<int>& nextVisit) {const int MOD = 1'000'000'007;int n = nextVisit.size();vector<long> s(n);for (int i = 0; i < n - 1; i++) {int j = nextVisit[i];s[i + 1] = (s[i] * 2 - s[j] + 2 + MOD) % MOD;}return s[n - 1];}
};

2908. 元素和最小的山形三元组 I

给你一个下标从 0 开始的整数数组 nums 。

如果下标三元组 (i, j, k) 满足下述全部条件，则认为它是一个山形三元组：

i < j < k
nums[i] < nums[j] 且 nums[k] < nums[j]
请你找出 nums 中元素和最小的山形三元组，并返回其元素和。如果不存在满足条件的三元组，返回 -1 。

示例 1：

输入：nums = [8,6,1,5,3]
输出：9
解释：三元组 (2, 3, 4) 是一个元素和等于 9 的山形三元组，因为：

2 < 3 < 4
nums[2] < nums[3] 且 nums[4] < nums[3]
这个三元组的元素和等于 nums[2] + nums[3] + nums[4] = 9 。可以证明不存在元素和小于 9 的山形三元组。
示例 2：

输入：nums = [5,4,8,7,10,2]
输出：13
解释：三元组 (1, 3, 5) 是一个元素和等于 13 的山形三元组，因为：

1 < 3 < 5
nums[1] < nums[3] 且 nums[5] < nums[3]
这个三元组的元素和等于 nums[1] + nums[3] + nums[5] = 13 。可以证明不存在元素和小于 13 的山形三元组。
示例 3：

输入：nums = [6,5,4,3,4,5]
输出：-1
解释：可以证明 nums 中不存在山形三元组。

提示：

3 <= nums.length <= 50
1 <= nums[i] <= 50

连wa四发，还得是灵神：

class Solution {
public:int minimumSum(vector<int>& nums) {int n = nums.size();vector<int> suf(n);suf[n - 1] = nums[n - 1];for (int i = n - 2; i > 1; i--) {suf[i] = min(suf[i + 1], nums[i]);}int ans = INT_MAX;int pre = nums[0];for (int j = 1; j < n - 1; j++) {if (pre < nums[j] && nums[j] > suf[j + 1]) {ans = min(ans, pre + nums[j] + suf[j + 1]);}pre = min(pre, nums[j]);}return ans == INT_MAX ? -1 : ans;}
};

前后缀分解题解：O(n) 前后缀分解，附题单（Python/Java/C++/Go/JS/Rust）

2952. 需要添加的硬币的最小数量

给你一个下标从 0 开始的整数数组 coins，表示可用的硬币的面值，以及一个整数 target 。

如果存在某个 coins 的子序列总和为 x，那么整数 x 就是一个可取得的金额。

返回需要添加到数组中的任意面值硬币的最小数量，使范围 [1, target] 内的每个整数都属于可取得的金额。

数组的子序列是通过删除原始数组的一些（可能不删除）元素而形成的新的非空数组，删除过程不会改变剩余元素的相对位置。

示例 1：

输入：coins = [1,4,10], target = 19
输出：2
解释：需要添加面值为 2 和 8 的硬币各一枚，得到硬币数组 [1,2,4,8,10] 。
可以证明从 1 到 19 的所有整数都可由数组中的硬币组合得到，且需要添加到数组中的硬币数目最小为 2 。
示例 2：

输入：coins = [1,4,10,5,7,19], target = 19
输出：1
解释：只需要添加一枚面值为 2 的硬币，得到硬币数组 [1,2,4,5,7,10,19] 。
可以证明从 1 到 19 的所有整数都可由数组中的硬币组合得到，且需要添加到数组中的硬币数目最小为 1 。
示例 3：

输入：coins = [1,1,1], target = 20
输出：3
解释：
需要添加面值为 4 、8 和 16 的硬币各一枚，得到硬币数组 [1,1,1,4,8,16] 。
可以证明从 1 到 20 的所有整数都可由数组中的硬币组合得到，且需要添加到数组中的硬币数目最小为 3 。

提示：

1 <= target <= 105
1 <= coins.length <= 105
1 <= coins[i] <= target

贪心

class Solution {
public:int minimumAddedCoins(vector<int>& coins, int target) {sort(coins.begin(), coins.end());long max_val = 0;int res = 0;for (int coin : coins) {while (coin > max_val + 1) {max_val += max_val + 1;res++;}max_val += coin;if (max_val >= target) {break;}}while (max_val < target) {max_val += max_val + 1;res++;}return res;}
};

331. 验证二叉树的前序序列化

序列化二叉树的一种方法是使用前序遍历。当我们遇到一个非空节点时，我们可以记录下这个节点的值。如果它是一个空节点，我们可以使用一个标记值记录，例如 #。

例如，上面的二叉树可以被序列化为字符串 “9,3,4,#,#,1,#,#,2,#,6,#,#”，其中 # 代表一个空节点。

给定一串以逗号分隔的序列，验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。

保证每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 ‘#’ 。

你可以认为输入格式总是有效的

例如它永远不会包含两个连续的逗号，比如 “1,3” 。
注意：不允许重建树。

示例 1:

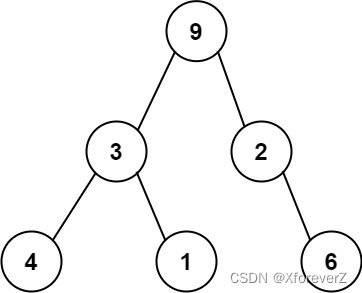
输入: preorder = “9,3,4,#,#,1,#,#,2,#,6,#,#”
输出: true
示例 2:

输入: preorder = “1,#”
输出: false
示例 3:

输入: preorder = “9,#,#,1”
输出: false

提示:

1 <= preorder.length <= 104
preorder 由以逗号 “，” 分隔的 [0,100] 范围内的整数和 “#” 组成

对于二叉树（不包括空节点），有 “所有非空节点提供2个出度和1个入度（根除外）；
所有空节点提供0个出度和1个入度”

class Solution {
public:bool isValidSerialization(string preorder) {stringstream ss(preorder);string node;int diff = 1;while (getline(ss, node, ',')) {diff -= 1;if (diff < 0) {return false;}if (node != "#") {diff += 2;}}return diff == 0;}
};

2810. 故障键盘

你的笔记本键盘存在故障，每当你在上面输入字符 ‘i’ 时，它会反转你所写的字符串。而输入其他字符则可以正常工作。

给你一个下标从 0 开始的字符串 s ，请你用故障键盘依次输入每个字符。

返回最终笔记本屏幕上输出的字符串。

示例 1：

输入：s = “string”
输出：“rtsng”
解释：
输入第 1 个字符后，屏幕上的文本是：“s” 。
输入第 2 个字符后，屏幕上的文本是：“st” 。
输入第 3 个字符后，屏幕上的文本是：“str” 。
因为第 4 个字符是 ‘i’ ，屏幕上的文本被反转，变成 “rts” 。
输入第 5 个字符后，屏幕上的文本是：“rtsn” 。
输入第 6 个字符后，屏幕上的文本是： “rtsng” 。
因此，返回 “rtsng” 。
示例 2：

输入：s = “poiinter”
输出：“ponter”
解释：
输入第 1 个字符后，屏幕上的文本是：“p” 。
输入第 2 个字符后，屏幕上的文本是：“po” 。
因为第 3 个字符是 ‘i’ ，屏幕上的文本被反转，变成 “op” 。
因为第 4 个字符是 ‘i’ ，屏幕上的文本被反转，变成 “po” 。
输入第 5 个字符后，屏幕上的文本是：“pon” 。
输入第 6 个字符后，屏幕上的文本是：“pont” 。
输入第 7 个字符后，屏幕上的文本是：“ponte” 。
输入第 8 个字符后，屏幕上的文本是：“ponter” 。
因此，返回 “ponter” 。

提示：

1 <= s.length <= 100
s 由小写英文字母组成
s[0] != ‘i’

简单模拟：

class Solution {
public:string finalString(string s) {string res;for (char c : s) {if (c == 'i') {reverse(res.begin(), res.end());} else {res.push_back(c);}}return res;}
};

894. 所有可能的真二叉树

给你一个整数 n ，请你找出所有可能含 n 个节点的真二叉树，并以列表形式返回。答案中每棵树的每个节点都必须符合 Node.val == 0 。

答案的每个元素都是一棵真二叉树的根节点。你可以按任意顺序返回最终的真二叉树列表。

真二叉树是一类二叉树，树中每个节点恰好有 0 或 2 个子节点。

示例 1：

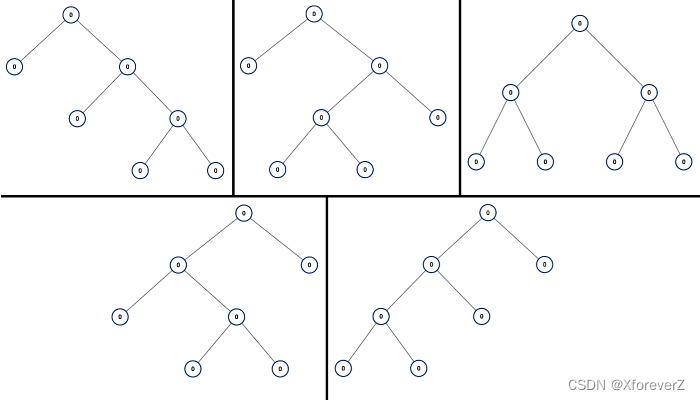
输入：n = 7
输出：[[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
示例 2：

输入：n = 3
输出：[[0,0,0]]

提示：

1 <= n <= 20

递归+DP:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:vector<TreeNode*> allPossibleFBT(int n) {if (n % 2 == 0)return {};vector<vector<TreeNode*>> dp(n + 1);dp[1].push_back(new TreeNode(0));for (int i = 3; i <= n; i += 2) {for (int j = 1; j < i; j += 2) {for (auto& left : dp[j]) {for (auto& right : dp[i - j - 1]) {TreeNode* root = new TreeNode(0);root->left = left;root->right = right;dp[i].push_back(root);}}}}return dp[n];}
};