matlab绘图实例-多线图

2024-04-01 17:58
文章标签 matlab 绘图 实例 线图

本文主要是介绍matlab绘图实例-多线图，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

  • matlab线条设定
  • 结果图常用设置(matlab)
  • 一个完整的五线图绘制模板(matlab)
    • 求多项式的根

matlab线条设定

matlab线条设定-官网
matlab线条设定2-官网

在这里插入图片描述

matlab默认风格

结果图常用设置(matlab)

linspace(起始值,终止值,元素个数)size(矩阵)   % 获取矩阵的行列数length(向量)  % 获取向量的长度data_box=xlsread('Data.xlsx');  % 将excel文件放在该matlab文件所在的路径中

一个完整的五线图绘制模板(matlab)

clc
clearx=linspace(-10,10,100);
y1=-x.^2;
y2=-2.*x.^2;
y3=-3.*x.^2;
y4=-4.*x.^2;
y5=-5.*x.^2;% matlab元组(cell)的使用：元组的一个元素可以存储一个矩阵
box{1}(:,1)=x; box{1}(:,2)=y1;
box{2}(:,1)=x; box{2}(:,2)=y2;
box{3}(:,1)=x; box{3}(:,2)=y3;
box{4}(:,1)=x; box{4}(:,2)=y4;
box{5}(:,1)=x; box{5}(:,2)=y5;%=====================================================================
figure(1);
plot(x,y1,'--r','LineWidth',2,'MarkerSize',7); hold on; 
plot(x,y2,'-.b','LineWidth',2,'MarkerSize',7); hold on; 
plot(x,y3,'-k','LineWidth',2,'MarkerSize',7); hold on; 
plot(x,y4,'--.g','LineWidth',2,'MarkerSize',10); hold on; 
plot(x,y5,':m','LineWidth',2,'MarkerSize',7); hold on; 
%---------------------------------------------------------------------
set(legend('$k=1$',...'$k=2$',...'$k=3$',...'$k=4$',...'$k=5$',...'Location','south'),'Interpreter','latex','FontSize',15,'fontname','Times New Roman')
% north   south   west   east 
%---------------------------------------------------------------------
set(gca,'FontSize',15,'fontname','Times New Roman')  %是设置刻度字体大小
% set(gca, 'YScale', 'log')
% set(gca, 'XScale', 'log')
set(gca, 'XLim', [-10,10])
set(gca, 'YLim', [-500,0])
xlabel('$x$','Interpreter','latex','FontSize',20,'fontname','Times New Roman')
ylabel('$y=kx^2$','Interpreter','latex','FontSize',20,'fontname','Times New Roman')
%---------------------------------------------------------------------
% 标注极值点
% [极值,极值点]=max(向量);              %获取最大值点和最大值   
% [~,极值点]=max(向量);                 %获取最大值点 
%---------------------------------------------------------------------
% 导出高分辨率(700)png图片
img1 =gcf;  %获取当前画图的句柄
print(img1, '-dpng', '-r700', './img1.png')         %=====================================================================
figure(2);
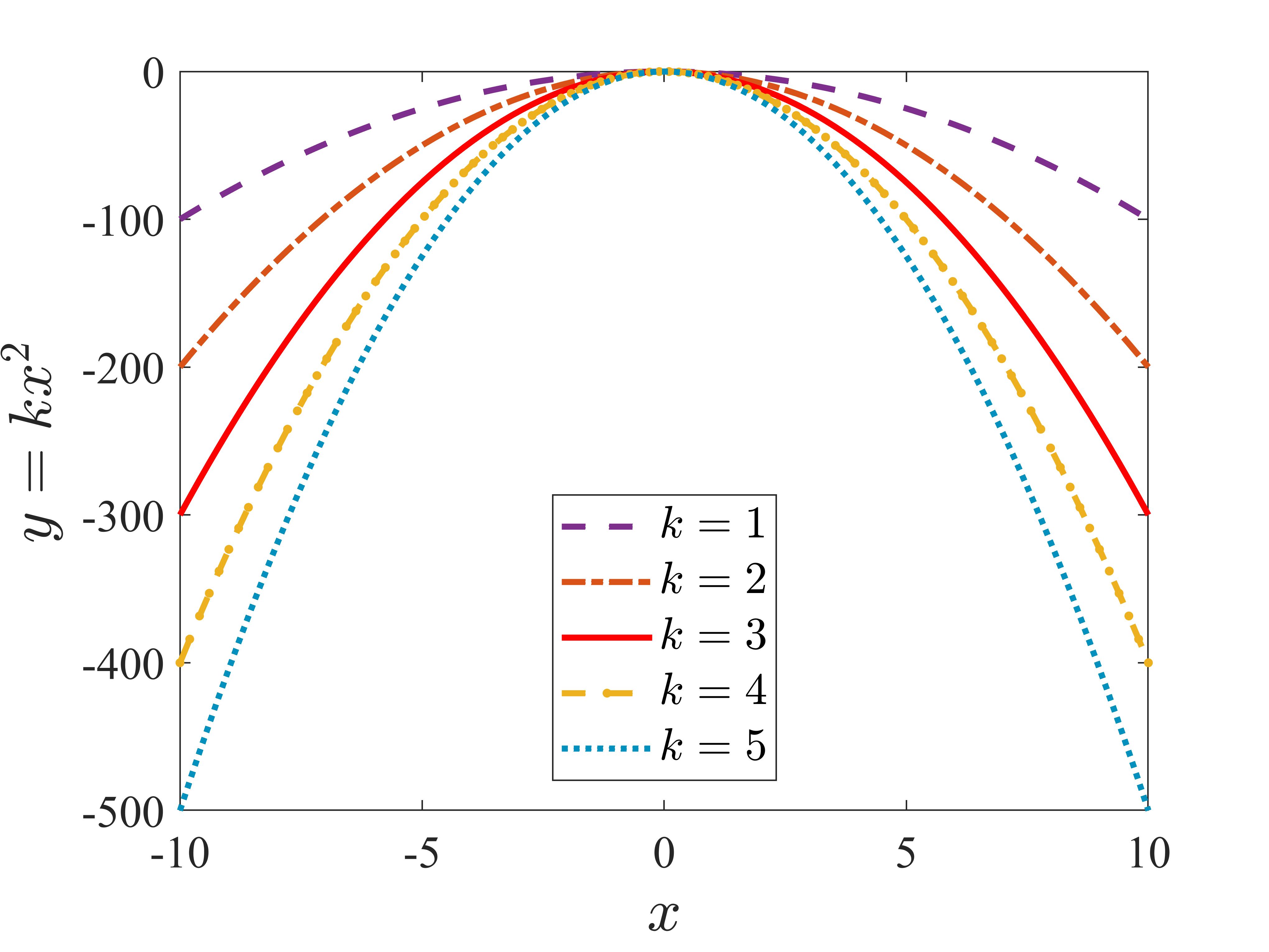
plot(box{1}(:,1),box{1}(:,2),'--','Color',[126,47,142]/255,'LineWidth',2,'MarkerSize',7); hold on; 
plot(box{2}(:,1),box{2}(:,2),'-.','Color',[217, 83, 25]/255,'LineWidth',2,'MarkerSize',7); hold on; 
plot(box{3}(:,1),box{3}(:,2),'-','Color',[255,0,0]/255,'LineWidth',2,'MarkerSize',7); hold on; 
plot(box{4}(:,1),box{4}(:,2),'--.','Color',[237, 177, 32]/255,'LineWidth',2,'MarkerSize',10); hold on; 
plot(box{5}(:,1),box{5}(:,2),':','Color',[0,144,189]/255,'LineWidth',2,'MarkerSize',7); hold on; 
%---------------------------------------------------------------------
set(legend('$k=1$',...'$k=2$',...'$k=3$',...'$k=4$',...'$k=5$',...'Location','south'),'Interpreter','latex','FontSize',15,'fontname','Times New Roman') 
% north   south   west   east 
%---------------------------------------------------------------------
set(gca,'FontSize',15,'fontname','Times New Roman')  %是设置刻度字体大小
% set(gca, 'YScale', 'log')
% set(gca, 'XScale', 'log')
set(gca, 'XLim', [-10,10])
set(gca, 'YLim', [-500,0])
xlabel('$x$','Interpreter','latex','FontSize',20,'fontname','Times New Roman')
ylabel('$y=kx^2$','Interpreter','latex','FontSize',20,'fontname','Times New Roman')
%---------------------------------------------------------------------
% 标注极值点
% [极值,极值点]=max(向量);              %获取最大值点和最大值   
% [~,极值点]=max(向量);                 %获取最大值点 
%---------------------------------------------------------------------
% 导出高分辨率(700)图片
img2 =gcf;  %获取当前画图的句柄
print(img2, '-dpng', '-r700', './img2.png')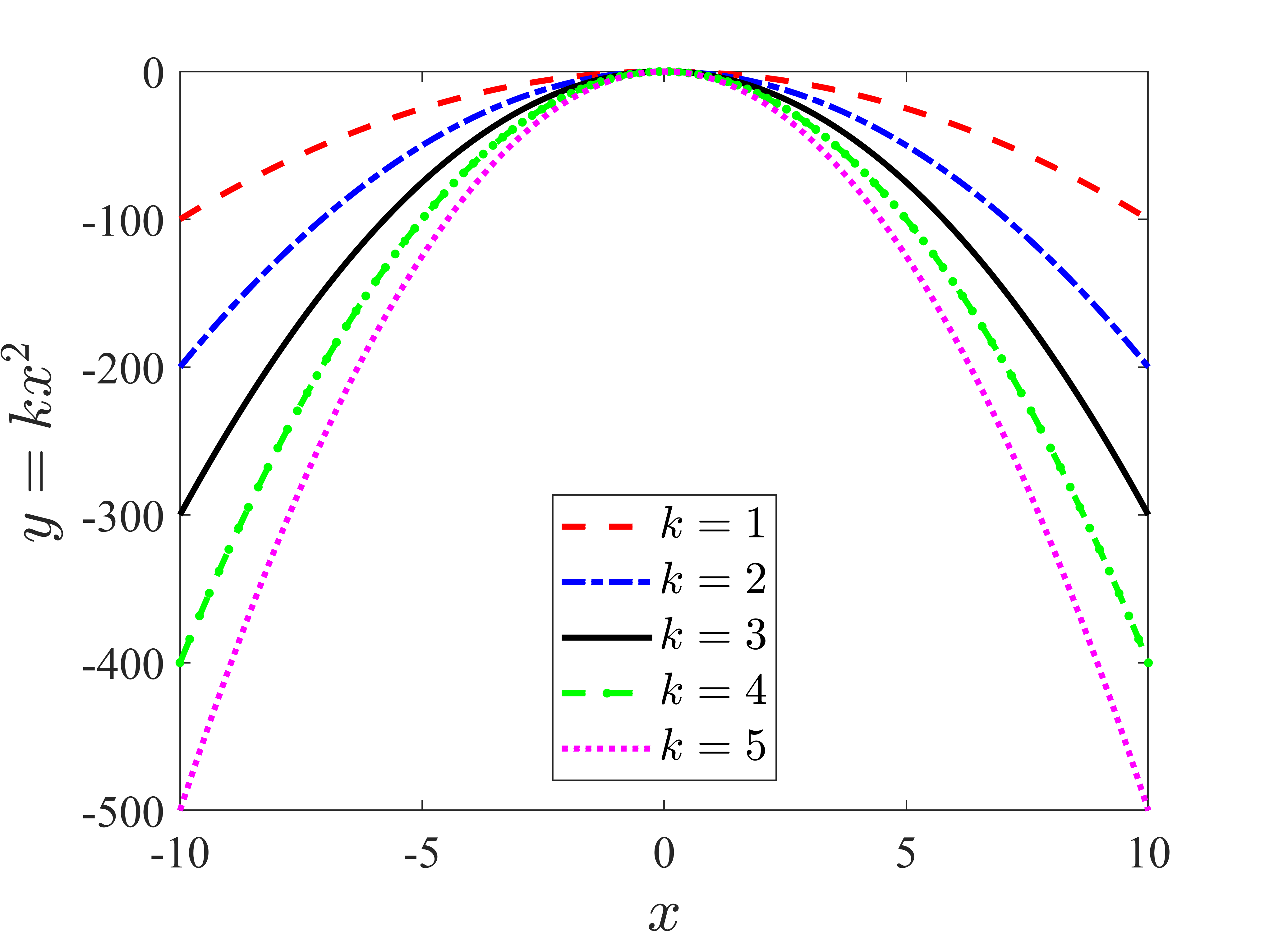
图片名称
图片名称 
% 结果显示精度设置format short
format long% 科学计数法
format short e
format long e% 没有科学计数法
format short g
format long g

设置刻度
xticks([0 5 10])
xticklabels({'x = 0','x = 5','x = 10'})中英文混用（tex解释器、部分字体设置）xlabel('再生骨料取代率\alpha Gpa{\fontname{Times New Roman} \alpha Gpa }','Interpreter','tex','FontSize',20,'fontname','Songti')
ylabel('$y=kx^2$','Interpreter','latex','FontSize',20,'fontname','Times New Roman')

annotation('arrow',[0.567857142857142 0.137499999999999],...[0.571428571428578 0.571428571428578]);
annotation('textbox',...[0.568857142857142 0.530952382655372 0.267865037279234 0.0809523792493911],...'String','$r_1=0.1 \to 10$',...'Interpreter','latex',...'FontSize',15,...'FitBoxToText','off',...'EdgeColor','none');

求多项式的根

% 求alpha2
% a7=8400*aa_*alpha1^2*etaa^2*fss^2*hh0*k*lambdak^2 - 637*EE*alpha1^2*k*lambdaE^2;
% a6=10800*aa_*alpha1^2*etaa^2*fss^2*hh0^2*lambdak^2 - 10800*Css0*alpha1^2*lambdaE^2;
% a5=0;
% a4=9600*aa_*alpha1*etaa*fss^2*hh0*k*lambdak^2;
% a3=10800*aa_*alpha1*etaa*fss^2*hh0^2*lambdak^2 + 150*EE*I1*k^3 - 180*EE*k^3*lambdak^2;
% a2=450*EE*I1*hh0*k^2 - 450*EE*hh0*k^2*lambdak^2;
% a1=1200*aa_*fss^2*hh0^2*k*lambdak^2 - 1800*I1*aa_*fss^2*hh0*k + 1800*I1*gg*hh0^2*k + 450*EE*I1*hh0^2*k - 1200*gg*hh0^2*k*lambdak^2 - 300*EE*hh0^2*k*lambdak^2;
% a0=1800*I1*Kss0*hh0^2;
% roots([a7 a6 a5 a4 a3 a2 a1 a0])   % 通过输入各阶系数求多项式的根。

factor_min=0.32;
factor_max=0.001;  
CircleNum=1000;
for jj=1:CircleNum+1    
factor = factor_min + (factor_max - factor_min)*((jj-1)/CircleNum)^2;
box(jj,1)=factor;  end

clc
clearx=linspace(-10,10,20);
y1=-x.^2;
y2=-2.*x.^2;
y3=-3.*x.^2;
y4=-4.*x.^2;
y5=-5.*x.^2;% matlab元组(cell)的使用：元组的一个元素可以存储一个矩阵
box{1}(:,1)=x; box{1}(:,2)=y1;
box{2}(:,1)=x; box{2}(:,2)=y2;
box{3}(:,1)=x; box{3}(:,2)=y3;
box{4}(:,1)=x; box{4}(:,2)=y4;
box{5}(:,1)=x; box{5}(:,2)=y5;%=====================================================================
figure(1);
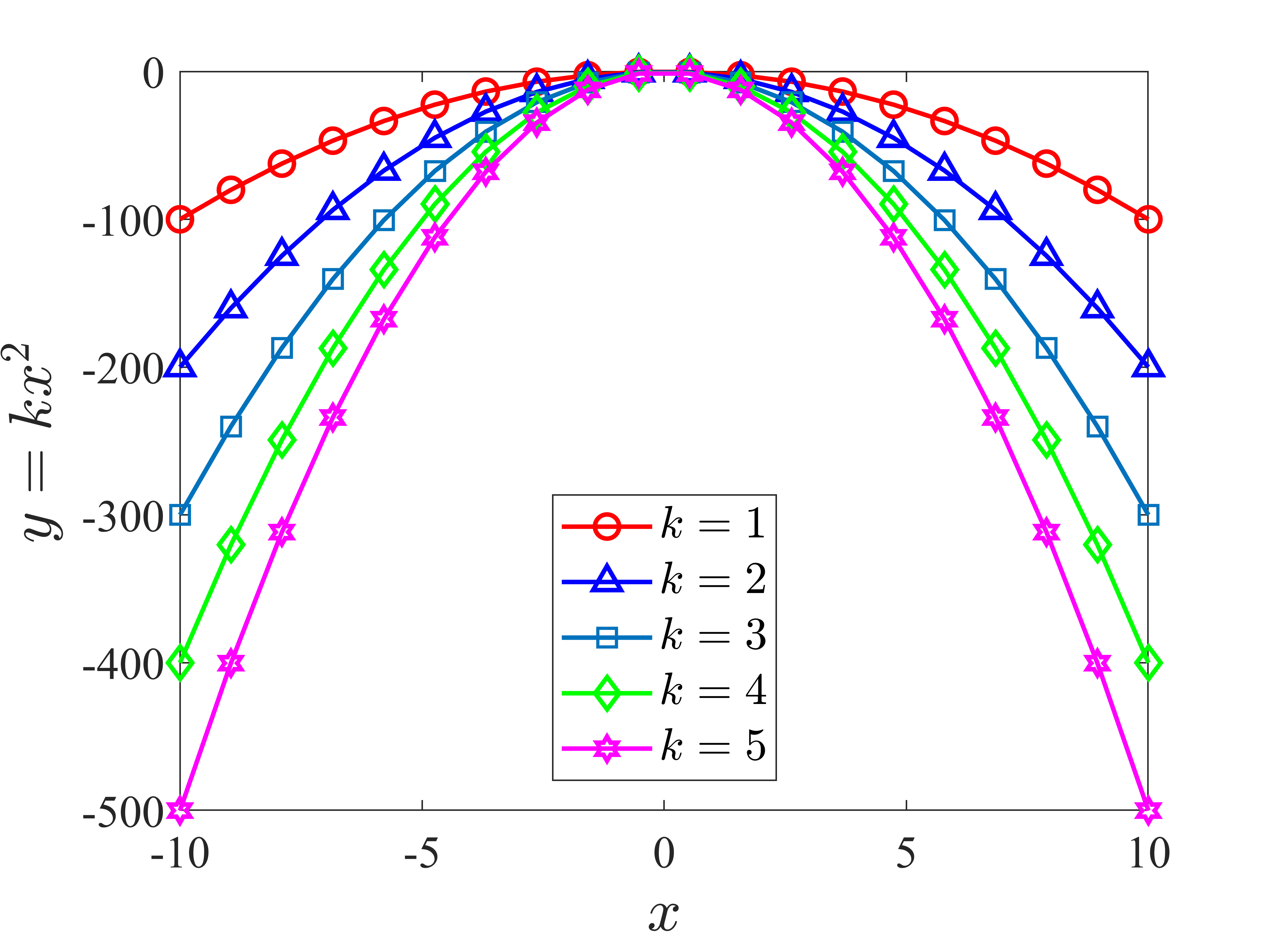
plot(x,y1,'-or','LineWidth',1.5,'MarkerSize',8); hold on; 
plot(x,y2,'-^b','LineWidth',1.5,'MarkerSize',8); hold on; 
plot(x,y3,'-s','LineWidth',1.5,'MarkerSize',8); hold on; 
plot(x,y4,'-dg','LineWidth',1.5,'MarkerSize',8); hold on; 
plot(x,y5,'-hm','LineWidth',1.5,'MarkerSize',8); hold on; 
%---------------------------------------------------------------------
set(legend('$k=1$',...'$k=2$',...'$k=3$',...'$k=4$',...'$k=5$',...'Location','south'),'Interpreter','latex','FontSize',15,'fontname','Times New Roman')
% north   south   west   east 
%---------------------------------------------------------------------
set(gca,'FontSize',15,'fontname','Times New Roman')  %是设置刻度字体大小
% set(gca, 'YScale', 'log')
% set(gca, 'XScale', 'log')
set(gca, 'XLim', [-10,10])
set(gca, 'YLim', [-500,0])
xlabel('$x$','Interpreter','latex','FontSize',20,'fontname','Times New Roman')
ylabel('$y=kx^2$','Interpreter','latex','FontSize',20,'fontname','Times New Roman')
%---------------------------------------------------------------------
% 标注极值点
% [极值,极值点]=max(向量);              %获取最大值点和最大值   
% [~,极值点]=max(向量);                 %获取最大值点 
%---------------------------------------------------------------------
% 导出高分辨率(700)png图片
img1 =gcf;  %获取当前画图的句柄
print(img1, '-dpng', '-r700', './img1.png')         %=====================================================================
图片名称

这篇关于matlab绘图实例-多线图的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/867783。

相关文章

SpringBoot+RustFS 实现文件切片极速上传的实例代码

SpringBoot+RustFS 实现文件切片极速上传的实例代码

《SpringBoot+RustFS实现文件切片极速上传的实例代码》本文介绍利用SpringBoot和RustFS构建高性能文件切片上传系统,实现大文件秒传、断点续传和分片上传等功能,具有一定的参考... 目录一、为什么选择 RustFS + SpringBoot？二、环境准备与部署2.1 安装 RustF
阅读更多...
MySQL的配置文件详解及实例代码

MySQL的配置文件详解及实例代码

《MySQL的配置文件详解及实例代码》MySQL的配置文件是服务器运行的重要组成部分,用于设置服务器操作的各种参数,下面：本文主要介绍MySQL配置文件的相关资料,文中通过代码介绍的非常详细,需要... 目录前言一、配置文件结构1.[mysqld]2.[client]3.[mysql]4.[mysqldum
阅读更多...
Java Stream流以及常用方法操作实例

Java Stream流以及常用方法操作实例

《JavaStream流以及常用方法操作实例》Stream是对Java中集合的一种增强方式,使用它可以将集合的处理过程变得更加简洁、高效和易读,：本文主要介绍JavaStream流以及常用方法... 目录一、Stream流是什么？二、stream的操作2.1、stream流创建2.2、stream的使用2.
阅读更多...
springboot项目中集成shiro+jwt完整实例代码

springboot项目中集成shiro+jwt完整实例代码

《springboot项目中集成shiro+jwt完整实例代码》本文详细介绍如何在项目中集成Shiro和JWT,实现用户登录校验、token携带及接口权限管理,涉及自定义Realm、ModularRe... 目录简介目的需要的jar集成过程1.配置shiro2.创建自定义Realm2.1 LoginReal
阅读更多...
Python跨文件实例化、跨文件调用及导入库示例代码

Python跨文件实例化、跨文件调用及导入库示例代码

《Python跨文件实例化、跨文件调用及导入库示例代码》在Python开发过程中,经常会遇到需要在一个工程中调用另一个工程的Python文件的情况,：本文主要介绍Python跨文件实例化、跨文件调... 目录1. 核心对比表格（完整汇总）1.1 自定义模块跨文件调用汇总表1.2 第三方库使用汇总表1.3 导
阅读更多...
MySQL多实例管理如何在一台主机上运行多个mysql

MySQL多实例管理如何在一台主机上运行多个mysql

《MySQL多实例管理如何在一台主机上运行多个mysql》文章详解了在Linux主机上通过二进制方式安装MySQL多实例的步骤,涵盖端口配置、数据目录准备、初始化与启动流程,以及排错方法,适用于构建读... 目录一、什么是mysql多实例二、二进制方式安装MySQL1.获取二进制代码包2.安装基础依赖3.清
阅读更多...
SpringBoot 异常处理/自定义格式校验的问题实例详解

SpringBoot 异常处理/自定义格式校验的问题实例详解

《SpringBoot异常处理/自定义格式校验的问题实例详解》文章探讨SpringBoot中自定义注解校验问题,区分参数级与类级约束触发的异常类型,建议通过@RestControllerAdvice... 目录1. 问题简要描述2. 异常触发1) 参数级别约束2) 类级别约束3. 异常处理1) 字段级别约束
阅读更多...
Apache Ignite缓存基本操作实例详解

Apache Ignite缓存基本操作实例详解

《ApacheIgnite缓存基本操作实例详解》文章介绍了ApacheIgnite中IgniteCache的基本操作,涵盖缓存获取、动态创建、销毁、原子及条件更新、异步执行,强调线程池注意事项,避免... 目录一、获取缓存实例（Getting an Instance of a Cache）示例代码：二、动态
阅读更多...
JSONArray在Java中的应用操作实例

JSONArray在Java中的应用操作实例

《JSONArray在Java中的应用操作实例》JSONArray是org.json库用于处理JSON数组的类,可将Java对象（Map/List）转换为JSON格式,提供增删改查等操作,适用于前后端... 目录1. jsONArray定义与功能1.1 JSONArray概念阐释1.1.1 什么是JSONA
阅读更多...
MySQL中的LENGTH()函数用法详解与实例分析

MySQL中的LENGTH()函数用法详解与实例分析

《MySQL中的LENGTH()函数用法详解与实例分析》MySQLLENGTH()函数用于计算字符串的字节长度,区别于CHAR_LENGTH()的字符长度,适用于多字节字符集（如UTF-8）的数据验证... 目录1. LENGTH()函数的基本语法2. LENGTH()函数的返回值2.1 示例1：计算字符串
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2