排序——选择排序(直接选择排序和堆排)

本文主要是介绍排序——选择排序(直接选择排序和堆排)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本专栏和大家分享关于排序的算法,其中有插入排（直接插入排序和希尔排序）、选择排序（直接选择排序和堆排）、交换排序（冒泡排序和快速排序）、归并排序以及其他非基于比较的排序

本文与大家分享选择排序

1.直接选择排序

优化：

时空复杂度:

稳定性:

2.堆排

向下调整的代码如下:

那么我们将数组向下调整后有什么用呢??

具体代码:

时空复杂度:

稳定性:

感谢您的访问!!!期待您的关注!!!

1.直接选择排序

实际上就是在遍历的时候,每次记录i下标之后的最小值,放到i下标位置,这样最后就能形成一个有序数组,比较容易理解,我们直接通过代码演示

public static void selectSort(int[] array){for(int i = 0; i < array.length - 1; i++){int maxIndex = i;for(int j = i + 1; j < array.length; j++){if(array[j] > array[maxIndex]){maxIndex = j;}}if(maxIndex != i){int tmp = array[maxIndex];array[maxIndex] = array[i];array[i] = tmp;}}}

但是时间复杂度太大！为O(N^2),是不稳定的排序

优化：

基于前面,我们可以在每一次遍历中不只是找最小值,而是最大值和最小值一起找

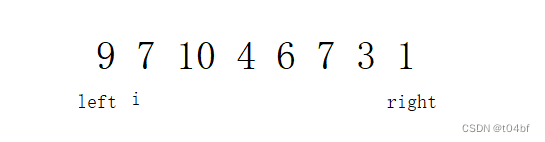
如图所示,我们定义一个左指针和一个右指针,接着利用i在left ~ right 里面遍历,找到一个最小值的下标和一个最大值的下标,将最小值与left的值进行交换,最大值与right的值进行交换,使得该区间的最小值和最大值分别在最左边和最右边的位置;接着 left ++,right--,缩小范围继续查找

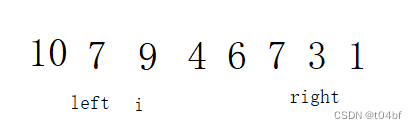
但是有一个细节问题需要考虑:

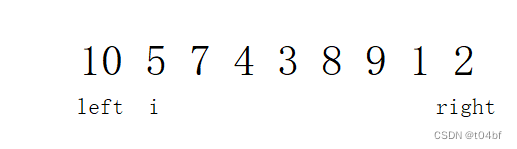
如果我们某一段区间出现这种情况,我们找出最小值为1,最大值为10,交换left的元素与最小值:

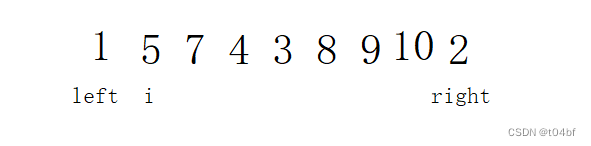
接着我们要交换最大值与right的元素就会发现最大值原本是left上面的10,现在变成了1.这是因为我们的最大值刚好是left上的元素,而原来left上的元素又被最小值交换到minIndex的位置去了,因此当我们的maxIndex == left的时候,我们在交换完最小值后,需要将maxIndex = minIndex,去交换后的地方找原来的最大值

    public static void OptimizedSelectSort(int[] array){int left = 0;int right = array.length-1;while(left < right){int minIndex = left;int maxIndex = left;for(int i = left+1; i <= right; i++){if(array[i] < array[minIndex]){minIndex = i;}if(array[i] > array[maxIndex]){maxIndex = i;}}swap(array,left,minIndex);if(maxIndex == left){maxIndex = minIndex;}swap(array,right,maxIndex);left++;right--;}}private static void swap(int[] array,int i,int j){int tmp = array[i];array[i] = array[j];array[j] = tmp;}

时空复杂度:

但是实际上时间复杂度还是O(N^2),分析时间复杂度的一种方法是考虑比较的次数。内层循环中，每个元素都可能与最大值和最小值进行比较，所以比较的次数仍然是 O(n^2)。虽然通过同时找到最大和最小值，每个元素可能会被比较两次，但这并不改变算法的时间复杂度。

空间复杂度为O(1)

稳定性:

是不稳定的排序:主要是因为在选择最小元素的过程中，相同元素的相对位置可能被打乱。

2.堆排

实际上认识了优先级队列的向下调整就能够理解堆排序

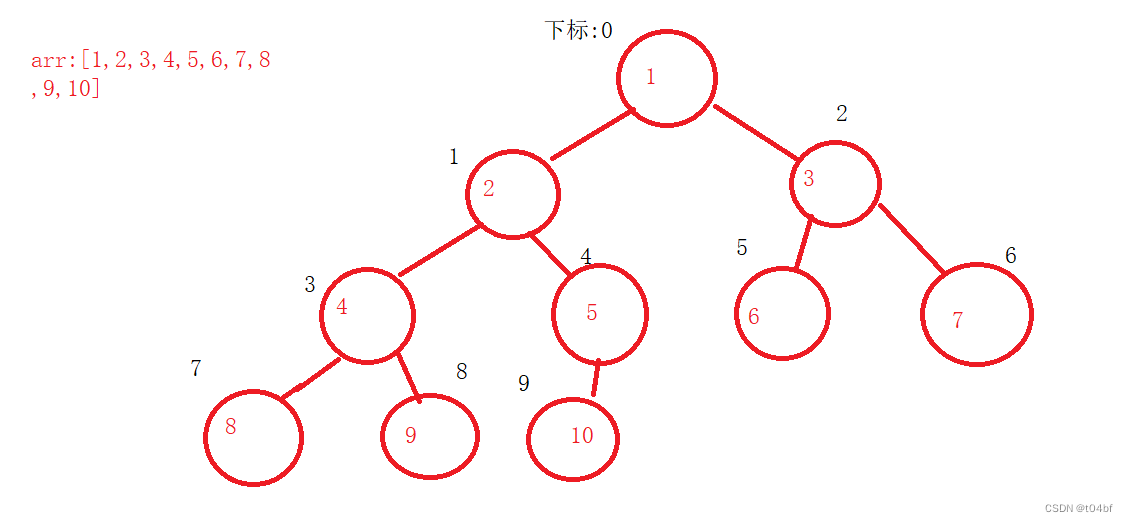
如果我们有如上图这样的数据,我们怎么将它设置为大根堆呢??

我们采用从最后一棵子树开始,依次向下调整的方法

假设每一棵子树的父亲节点下标为parent,子节点为child,那么最后一棵子树的子节点下标为 arr.length - 1,就能得到最后一棵子树的父亲节点下标为parent = (child - 1) / 2,即(arr.length - 1 ) /2 ;那么我们就从(arr.length - 1 ) /2 这个节点往前遍历,直到parent < 0,每次遍历都要针对每课子树进行向下调整

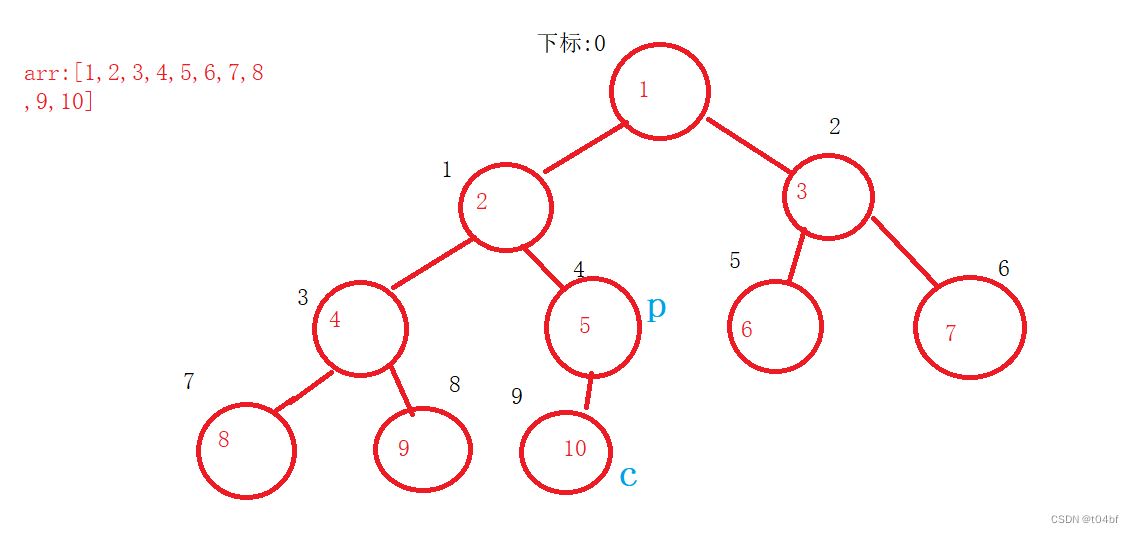
由于我们要建立的是大根堆,那么要求每棵子树的父亲节点都要大于任意一个子节点,那么我们就要在子节点里面找到一个最大的子节点,判断这个子节点是否大于父亲节点,如果大于,则交换

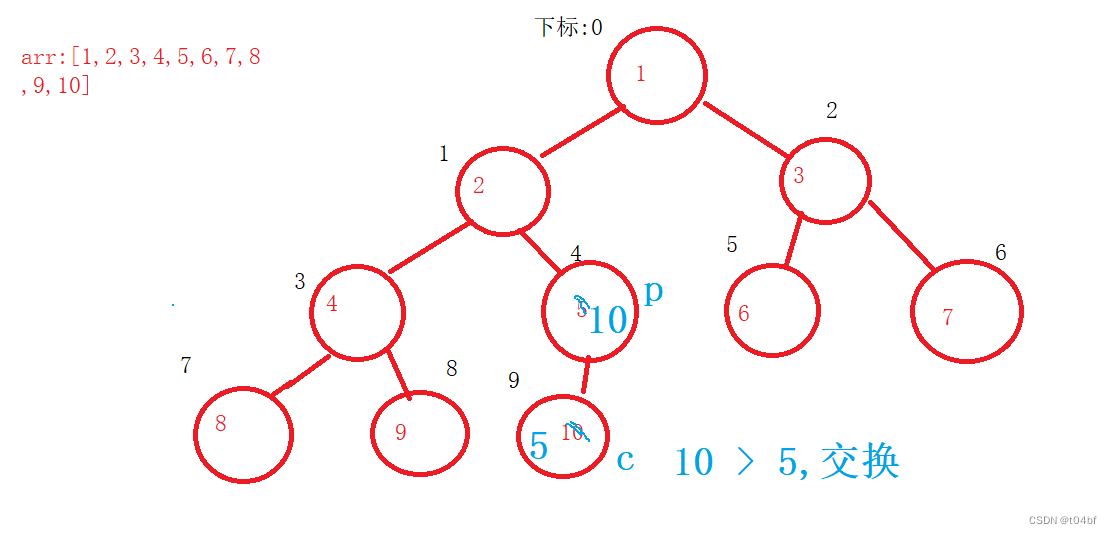
以4下标为根节点的子树已经判断完了,接下来parent--,判断以3下标为节点的所有子树

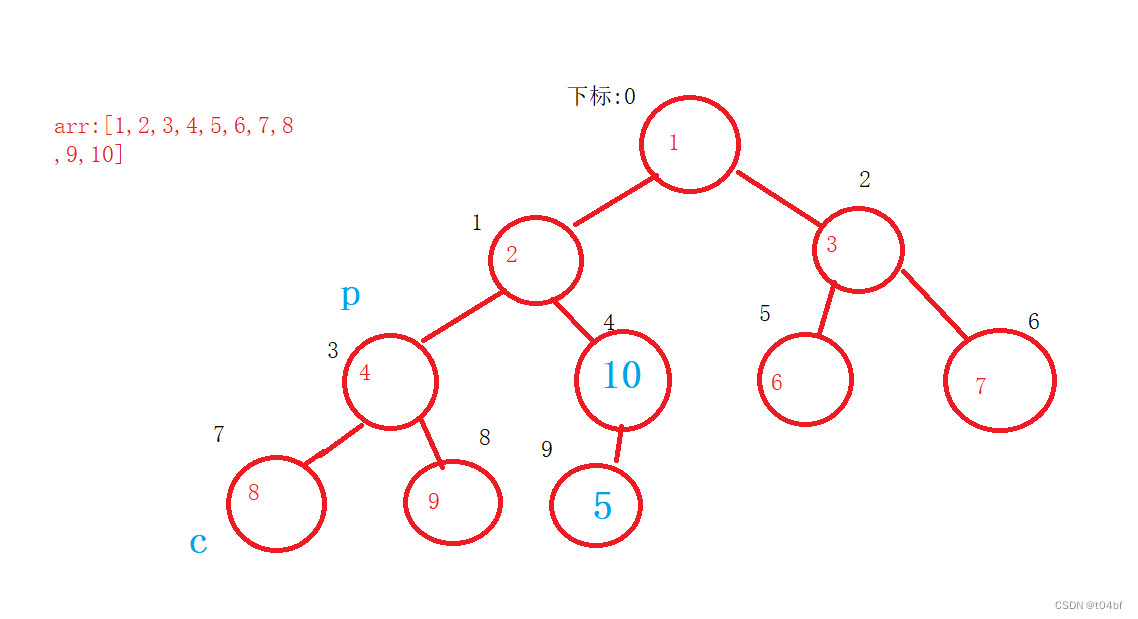
找到子节点中最大的一个,即为8,判断 9 > 4,那么9 与 4交换

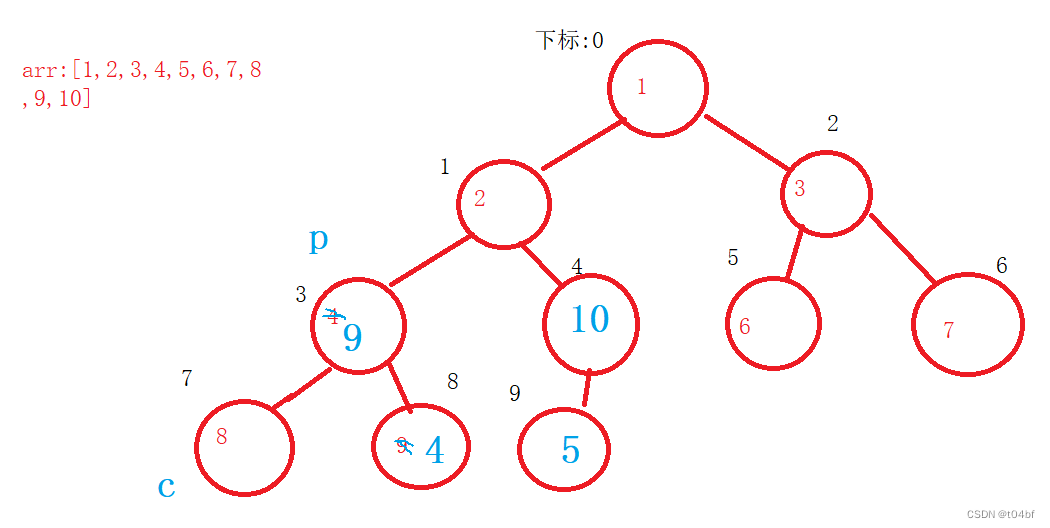
那么以3下标为根节点的子树也就判断完了,接下来判断以2为节点的子树

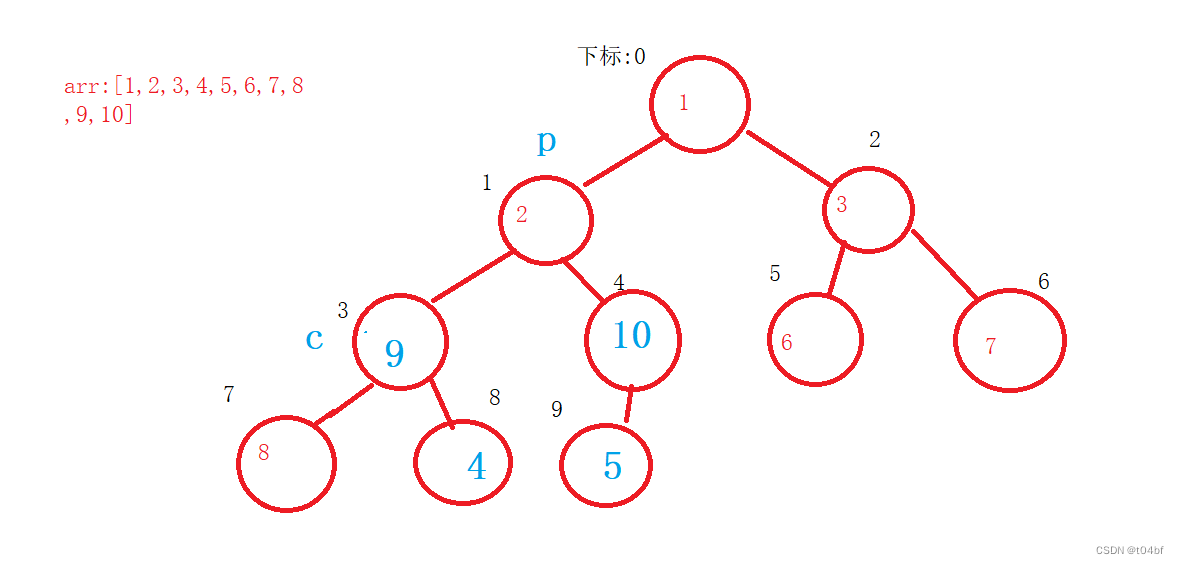
可以看到,此时子树就不止一棵了,我们先判断以2为父亲节点的树,找到子节点中最大的,为10, 10 > 2,那么10与2交换,

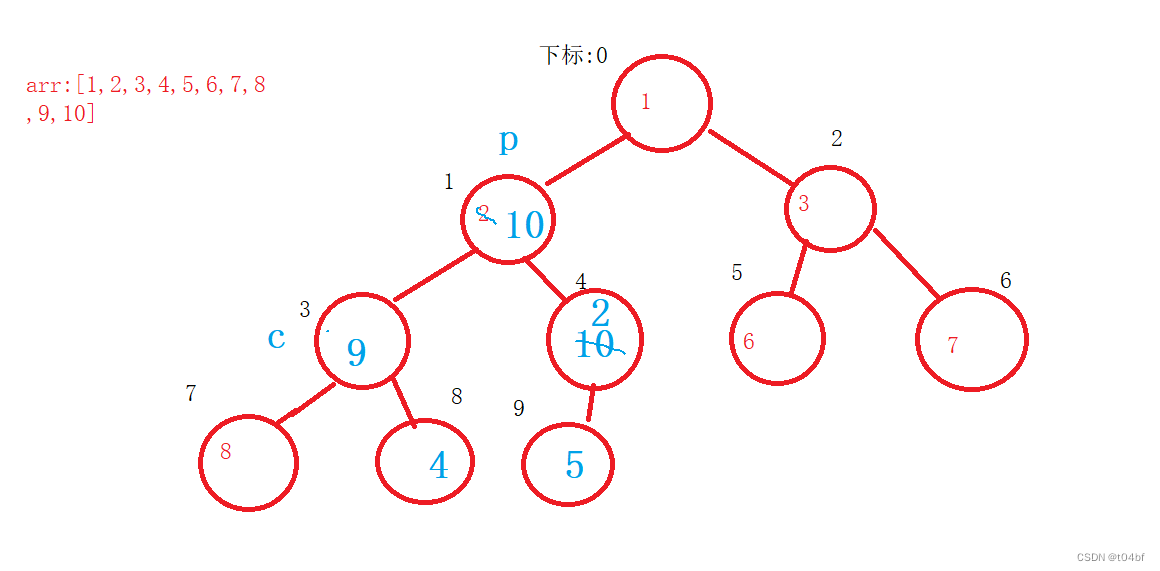
此时我们会发现,交换完后,以4下标为父亲节点的树就不满足大根堆的要求了,因此我们要让parent = child,再继续向下调整,直到每课子树都满足向下调整的要求,交换完后是这样的

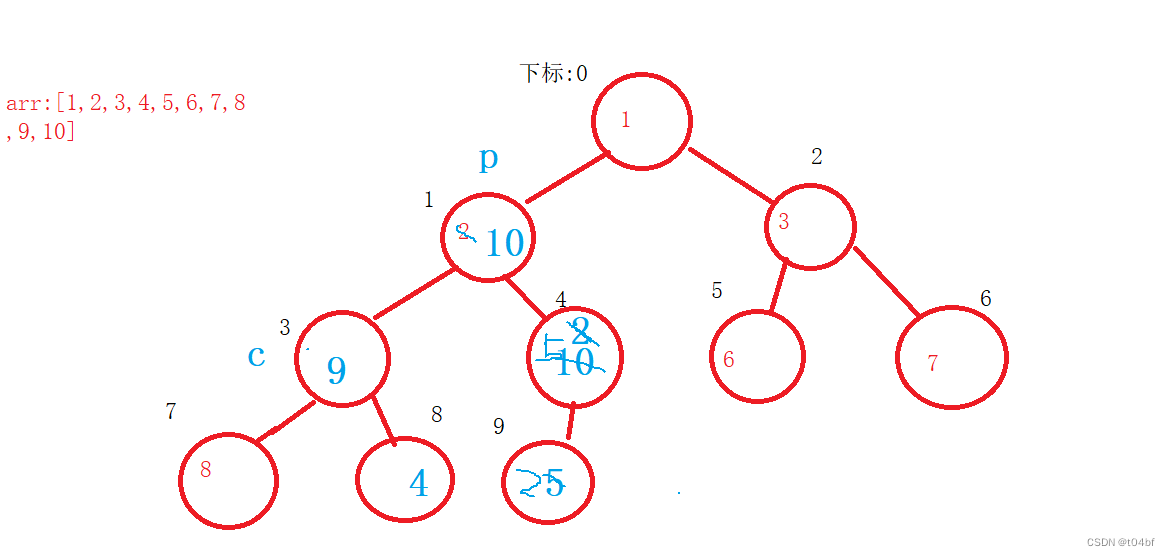
然后parent继续--,继续重复上述的流程即可

向下调整的代码如下:

public static void heap(int[] array){for(int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--){siftDown(array,parent);}}private static void siftDown(int[] array,int parent){int child = 2 * parent + 1;while(child < array.length){if(child + 1 < array.length && array[child] < array[child+1]){//找到子节点最大的一个child++;}if(array[parent] < array[child]){swap(array,parent,child);parent = child;child = 2 * parent + 1;}else{break;//不需要交换则说明这颗子树满足条件}}}private static void swap(int[] array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}

那么我们将数组向下调整后有什么用呢??

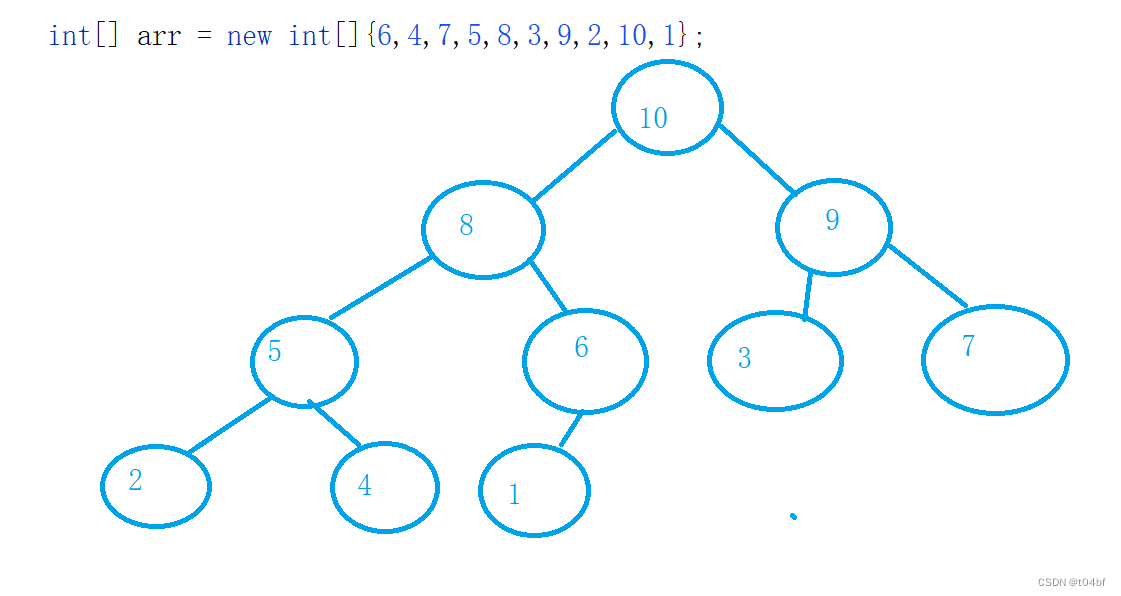
如图所示,我们以数组{6,4,7,5,8,3,9,2,10,1}建立完大根堆后,堆顶元素就是数组里面最大的元素,那么我们如果要得到增序列,就可以将堆顶元素与最后一个元素进行交换,就是将最大的数往后放接着再次进行向下调整,但是此时的向下调整不包括刚刚放进去的最大值,这样我们就能将第二大的元素通过向下调整放到堆顶,再次进行交换...依次类推

具体代码:

 public static void heapSort(int[] array){if(array.length == 0){return;}for(int parent = (array.length-1-1) / 2; parent >= 0; parent--){siftDown(array,parent,array.length);}int end = array.length - 1;while(end > 0){swap(array,0,end);siftDown(array,0,end);end--;}}private static void siftDown(int[] array,int parent,int end){int child = 2 * parent + 1;while(child < end){if(child + 1 < end&& array[child] < array[child+1]){//找到子节点最大的一个child++;}if(array[parent] < array[child]){swap(array,parent,child);parent = child;child = 2 * parent + 1;}else{break;//不需要交换则说明这颗子树满足条件}}}private static void swap(int[] array,int i,int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}