CCPC2020 - 秦皇岛 - G. Good Number （数学）

本文主要是介绍CCPC2020 - 秦皇岛 - G. Good Number （数学），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

亚历克斯喜欢数字。

亚历克斯认为，正整数 $x$ 是好数，当且仅当 $\lfloor \sqrt[k]{x} \rfloor$ 整除 $x$ 。

你能告诉他不超过 $n$ 的正整数的个数吗？

输入

输入的第一行给出了测试用例的数量 $\le T \le 10)$ 。接下来是 $T$ 个测试用例。

对于每个测试用例，唯一的一行包含两个整数 $n$ 和 $\le n,k \le 10^9)$ 。

输出

对于每个测试用例，输出一行包含 "Case #x: y"的内容，其中 $\texttt{x}$ 是测试用例编号(从 $1$ 开始)， $\texttt{y}$ 是答案。

Example
input

2
233 1
233 2

output

Case #1: 233
Case #2: 43

这道题需要找规律，如果打表把所有的能够符合要求的数打出来的话，就会发现他们有的是对应了连续几个 $\lfloor \sqrt[k]{x} \rfloor$ ：
比如n为250，k为2的情况。
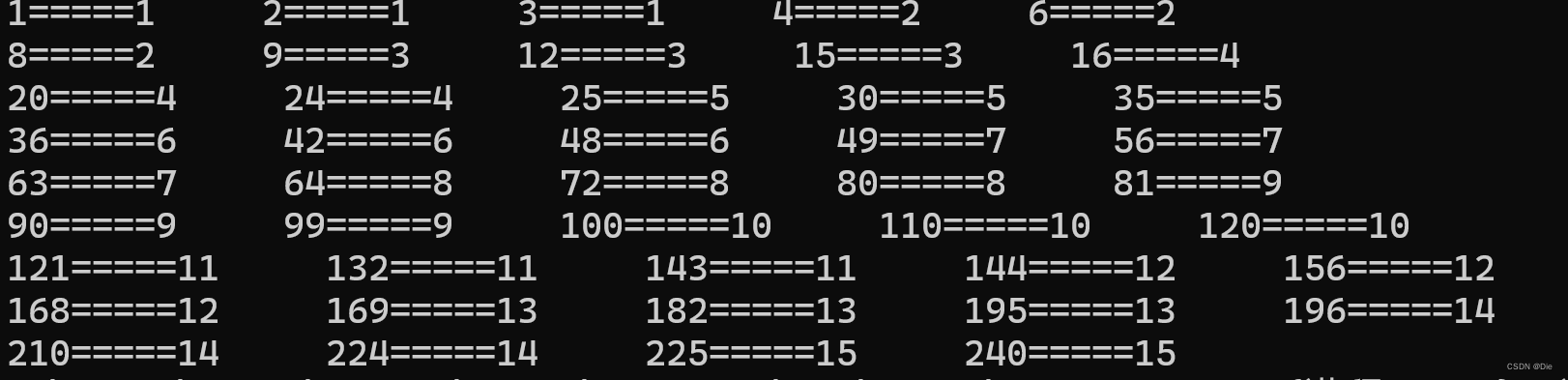
在这里插入图片描述
就比如 $9$ 对应 $3$ ， $12$ 、 $15$ 也对应 $3$ 。
这里这么看， $3$ 的 $k$ 次方对应了 $9$ ，而 $4$ 的k次方对应了 $16$ 。
所以发现 $n^k , (n+1)^k)$ 这个区间内开 $k$ 次方，下取整后能够得到的数都是 $n$ 。所以就只需要求每一个区间内有多少能够整除 $n$ 的数，我们看到 $9$ 到 $12$ 到 $15$ ，每个都相差了 $3$ ，所以对于区间 $[a, b]$ ，能够被 $n$ 整除的个数就是 $\lfloor\frac{b}{n}\rfloor - \lfloor\frac{a-1}{n}\rfloor$ 。

这么算完之后，如果遇见了 $x^k <= n <= (x+1)^k$ 的情况，那么就在这一次取完答案之后跳出。

并且注意，因为题目给出要求 $k$ 是小于等于 $1 e 9$ ，但是当 $k$ 大于等于 $31$ 的时候，整个 $in t$ 范围内的数都只能下取整到 $1$ 了，所以这种情况直接特判。
还有 $k = 1$ 的时候，直接输出 $n$ 。

至于下取整，直接强转 $in t$ 即可。

#include<iostream>
#include<map>
#include<cmath>
using namespace std;
#pragma warning (disable:4996)
#define ll long longll qmi(ll a, ll k) {//需要快速幂，不然TLEll res = 1;while (k) {if (k & 1)res = (ll)res * a;k >>= 1;a = (ll)a * a;}return res;
}int main() {int T; cin >> T;for (int cases = 1; cases <= T; cases++) {int n, k; cin >> n >> k;if (k == 1 || k >= 31) {printf("Cases #%d: %d\n", cases, n);continue;}int res = 0;int i = 0;while (++i) {ll l = qmi(i, k), r = qmi(i + 1, k) - 1;if (l <= n && n <= r) {if (l == n)res++;else {res += (n - l) / i + 1;}break;}res += (r - l) / i + 1;}printf("Case #%d: %d\n", cases, res);}return 0;
}