Java_20 元素和最小的山形三元组

本文主要是介绍Java_20 元素和最小的山形三元组，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

元素和最小的山形三元组

给你一个下标从 0 开始的整数数组 nums 。

如果下标三元组 (i, j, k) 满足下述全部条件，则认为它是一个 山形三元组 ：

• i < j < k
• nums[i] < nums[j] 且 nums[k] < nums[j]

请你找出 nums 中 元素和最小 的山形三元组，并返回其 元素和 。如果不存在满足条件的三元组，返回 -1 。

示例 1：

输入：nums = [8,6,1,5,3]
输出：9
解释：三元组 (2, 3, 4) 是一个元素和等于 9 的山形三元组，因为： 
- 2 < 3 < 4
- nums[2] < nums[3] 且 nums[4] < nums[3]
这个三元组的元素和等于 nums[2] + nums[3] + nums[4] = 9 。可以证明不存在元素和小于 9 的山形三元组。

示例 2：

输入：nums = [5,4,8,7,10,2]
输出：13
解释：三元组 (1, 3, 5) 是一个元素和等于 13 的山形三元组，因为： 
- 1 < 3 < 5 
- nums[1] < nums[3] 且 nums[5] < nums[3]
这个三元组的元素和等于 nums[1] + nums[3] + nums[5] = 13 。可以证明不存在元素和小于 13 的山形三元组。

示例 3：

输入：nums = [6,5,4,3,4,5]
输出：-1
解释：可以证明 nums 中不存在山形三元组。

提示：

• 3 <= nums.length <= 50
• 1 <= nums[i] <= 50

我的解答

思路：先将整个数组从小到大排序，以确保元素和最小；在排序的过程中，也将其一开始对应的下标改变顺序

再进行一下条件判断

• i < j < k
• nums[i] < nums[j] 且 nums[k] < nums[j]

第一次排序算法写错了，出错

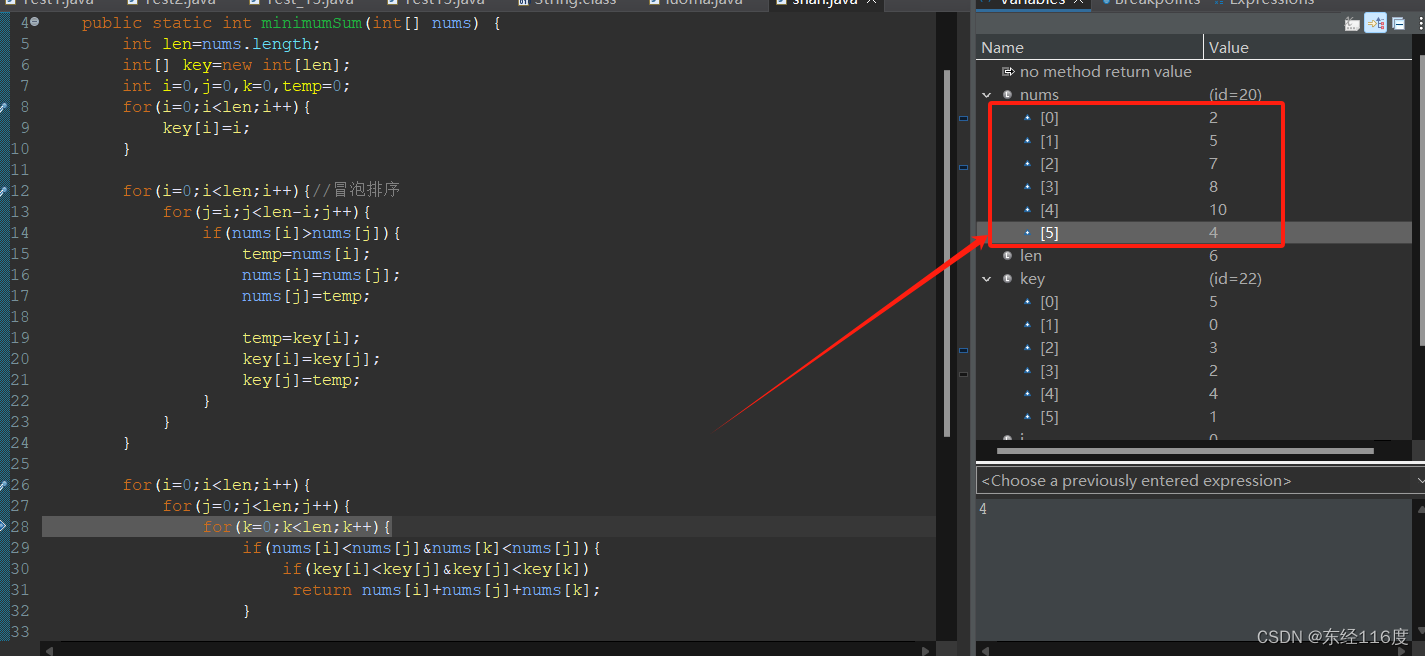
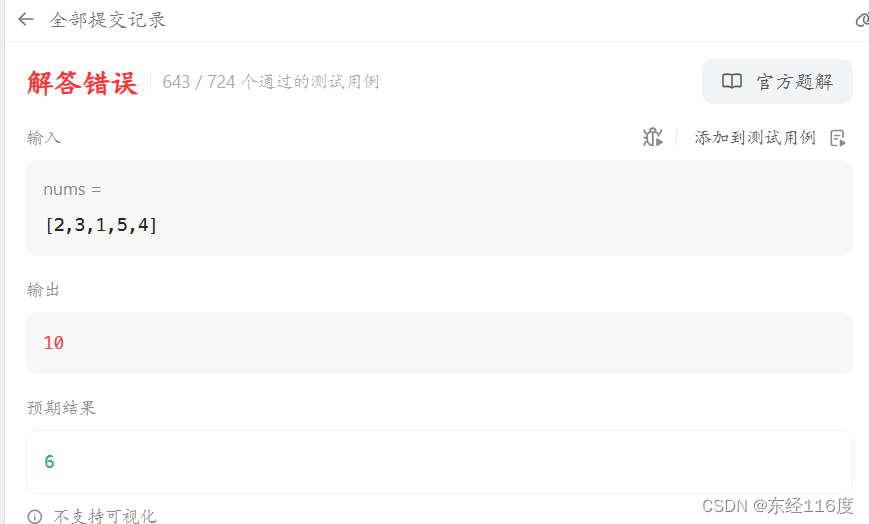
 修改后提交，依旧存在问题，没法百分百通过

class Solution {public int minimumSum(int[] nums) {int len=nums.length;int[] key=new int[len];int i=0,j=0,k=0,temp=0;for(i=0;i<len;i++){key[i]=i;}for(i=0;i<len-1;i++){//冒泡排序for(j=0;j<len-1-i;j++){if(nums[j]>nums[j+1]){temp=nums[j];nums[j]=nums[j+1];nums[j+1]=temp;temp=key[j];key[j]=key[j+1];key[j+1]=temp;}}}for(i=0;i<len;i++){for(j=0;j<len;j++){for(k=0;k<len;k++){if(nums[i]<nums[j]&nums[k]<nums[j]){if(key[i]<key[j]&key[j]<key[k])return nums[i]+nums[j]+nums[k];}}}}return -1;}
}

 

官方题解

元素和最小的山形三元组 I

力扣官方题解

方法一：枚举

思路与算法

我们直接按照题目的要求进行模拟，枚举所有三元组即可。

class Solution {public int minimumSum(int[] nums) {int n = nums.length, res = 1000;for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {for (int k = j + 1; k < n; k++) {if (nums[i] < nums[j] && nums[k] < nums[j]) {res = Math.min(res, nums[i] + nums[j] + nums[k]);}}}}return res < 1000 ? res : -1;}
}

复杂度分析

• 时间复杂度：O(n3)O(n^3)O(n3)，其中 nnn 是数组的长度。
• 空间复杂度：O(1)O(1)O(1)。

方法二：数组

思路与算法

我们从左到右遍历，来求出前缀数组中的最小值，用 left[i]\textit{left}[i]left[i] 来表示前 iii 个数字的最小值。

然后我们从右到左遍历，用 right\textit{right}right 来表示当前数字右边的最小值。
如果一个数比左右两边最小值大时，说明找到一个山形三元组，并更新当前山形三元组的最小元素和。

最后我们返回最小元素和即可。

class Solution {
public:int minimumSum(vector<int>& nums) {int n = nums.size(), res = 1000, mn = 1000;vector<int> left(n);for (int i = 1; i < n; i++) {left[i] = mn = min(nums[i - 1], mn);}int right = nums[n - 1];for (int i = n - 2; i > 0; i--) {if (left[i] < nums[i] && nums[i] > right) {res = min(res, left[i] + nums[i] + right);}right = min(right, nums[i]);}return res < 1000 ? res : -1;}
};

复杂度分析

• 时间复杂度：O(n)O(n)O(n)，其中 nnn 是数组的长度。
• 空间复杂度：O(n)O(n)O(n)，其中 nnn 是数组的长度。

 

这篇关于Java_20 元素和最小的山形三元组的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---