本文主要是介绍密码学期末,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
密码学简答题
1、解释PoW、PoS、DPoS、PBFT四种共识算法的原理

(1)PoW的原理是,节点通过解决数学难题来竞争获得记账权,谁先解决问题,谁就获得记账权,这个过程也就是挖矿的过程。由于解决问题需要大量的计算,所以矿工需要投入大量的电力和硬件设备
(2)PoS的原理是,节点根据其持有的币龄和币量来投票选举出一定数量的代理节点,由这些代理节点来代替全体节点进行记账。币龄越长,币量越多的节点,被选为代理节点的概率越大
(3)DPoS(委托权益证明)的原理是,节点选举出一定数量的超级节点,由这些超级节点来代替全体节点进行记账。超级节点的数量通常远远小于全体节点的数量,这样可以大大提高系统的吞吐量
(4)PBFT的原理是,每个节点都维护了相同的状态机副本复制,通过预准备阶段、准备阶段、提交阶段三个阶段来实现共识。在预准备阶段,主节点向其他节点发送请求;在准备阶段,其他节点对请求进行回应;在提交阶段,主节点根据回应情况决定是否提交事务。这种算法的优点是具有高吞吐量、低延迟和容错性密码学中,常见的5种2、攻击方式有哪些?
(1)唯密文攻击:已知密码算法及明文统计特性,通过密文分析出明文或者密钥
(2)已知明文攻击:已知明文攻击是指密码分析者已经知道了一段明文和对应的密文,以此来推导出密钥
(3)选择密文攻击:密码分析者选出两个或多个同一密钥加密的密文,推到出密钥
(4)选择明文攻击:密码分析者可以选择两个或多个明文,并知道它们对应的密文,以此来推导出密钥
(5)蛮力攻击:尝试所有可能的密钥,直到找到正确的那一个为止
3、有限域和普通的环有什么区别?
如果一个环中的所有非零元素都有乘法逆元,那么它就是一个除环,而如果一个除环满足乘法交换率,那么它就是一个域。
环:(1)加法阿贝尔群(交换律、结合律) (2)满足封闭性、结合率 (9)满足分配率
有限域:有限个元素的特殊域,元素的个数称为有限域的阶
区别:(1)环中的元素可能没有乘法逆元 (2)环中的元素不能进行乘法运算
4、RSA的公私钥制作步骤和加解密过程?
(1)选择两个质数p,q
(2)质数相乘N
(3)欧拉函数T = (p-1)*(q-1)
(4)选公钥E(质数,1<E<T,不是T的因子)
(5)算私钥 D
-
密码学如何用于改进共识算法?请结合具体的共识算法进行说明
(1)通过数字签名和哈希函数等技术,确保参与者的身份
(2)通过零知识证明、同态加密技术实现隐私保护
5、10阶循环群有多少个生成元。写出计算过程 (互质)
Z10={0,1,2…,9} ; 群的阶为 10 ;群是循环群,其生成元个数:Φ(10) = 4 {0,1,2…,9}中与10互素的有 1,3,7,9 四个 Z10可表示为<1> 则生成元为 1^1, 1^3,1^7,1^9(加法群),即1,3,7,9四个
6、什么是除环?
环就是满足(1)加法阿贝尔群(2)封闭性、结合律(3)满足分配率
除环就是一个环中的所有非零元素都有乘法逆元
7、什么是乘法逆元?

费马小定理求乘法逆元
扩展欧几里得算法:
我们都知道模就是余数,比如12%5=12-5 * 2=2,18%4=18-4*4=2。(/是程序运算中的除)可知a%b=a-(a/b)b
那么ax≡1 (mod p)即ax-yp=1.把y写成+的形式就是ax+py=1,为方便理解下面我们把p写成b就是ax+by=1。就表示x是a的模b乘法逆元,y是b的模a乘法逆元。然后就可以用扩展欧几里得求了。 a-(a/b)b = 1 , a = 3 , 一个一个试吧 , 哎!
8、什么是整环?
满足封闭性、结合律的就是乘法半群
任何非零整数与零相乘的结果都为0,且整数之间可以按照交换群的规则进行加法运算
9、循环群和生成元是什么?
若<G,※>为群,如果G中存在一个元素a,使得G中的任意元素都是a的幂,那么称该群为循环群,而元素a被称为该循环群的生成元
10、在DES的第6个S盒中,S(101111) = ?(结果使用2进制表示,写出计算过程)
取首位+末位组成二进制串,转换成十进制,作为行
其他位组成二进制串,转换成十进制,作为列
11、置换密码是什么?它改变的是明文的位置还是明文的内容 ?
对明文字符或者字符组进行移动的密码
明文的字母不变,但是顺序被打乱了
12、门限签名
13、不属于单表代换密码 ? (1)公钥密码 (2)维吉尼亚密码(多表代换密码)
(1)军事密码的巅峰代表是:恩尼格玛机,破译它的是香农
(2)古典密码中,两个主要操作是代换和置换
(3)密码学第二次历史飞跃RSA的出现
(4)《保密系统的通信理论》这篇论文把密码学置于监视的数学基础之上,标志着密码学作为一门学科的形成,该论文的作者是:香农
(5)一个密码体制至少包含:明文、密文、密钥、加密和解密算法
(6)凯撒密码相当于key=3的移位密码
(7)分组密码的安全性设计原则是扩散性和混淆性。S盒是非线性部分,主要实现混淆性,置换P是线性部件,主要实现扩散性。
(8)DES的分组长度是64比特,有效密钥长度为56比特,加密轮数为16(64,56,16)
(9)AES-128的分组长度是128比特,密钥长度为128比特,加密轮数为10(128,128,10)
(10)有限域的正确表示: GF(q) , 域一定没有零因子
(11)古典密码最早出现于第一次世界大战,错误的
(12)如果DES加密使用的轮密钥为k1 k2 k3... k16,则DES解密时第一轮使用的密钥为K16
12、采用凯撒密码,对明文love进行加密,得到的密文是什么?要求写出计算过程
k=3的移位密码
13、在RSA公钥加密体制中,p=7,q=11。用于解密的私钥d=7。求公钥是多少?对消息2进行加密得到的密文是多少?要求写出计算过程
(D*E)%7 == 1
14、在Diffie-Hellman密钥交换协议中,设p=11,g=2(原根)。Alice和Bob之间分别选取随机数a=9,b=3。则A和B之间建立的共享密钥k为多少?写出计算过程。
DH算法属于公钥加密算法,加解密数据使用对称密码技术,密钥管理使用公钥密码技术
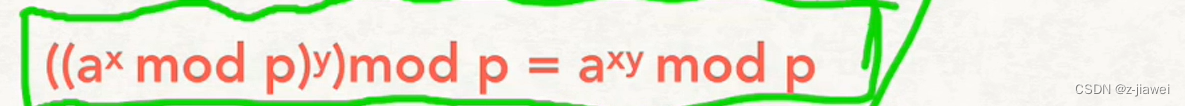

15、什么是乘法阶 ?

16、什么是子群?针对阿贝尔群写出两种构造子群的方法。
设(G,x)是群,H是G的非空子集,如果(H,x)是一个群,则称(H,x)是(G,x)的子群
针对阿贝尔群构造子群:
(1)G是阿贝尔群,m属于Z,则G^m = {a^m | a 属于G}是G的子群
(2)G是阿贝尔群,m属于Z,G{m} := {a属于G | a ^m = e} 是G的子群
17、整数群如何构造子群?写出两种构造整数子群的方法。
(1)H是Z的子群,存在唯一的非负整数m,使得H = mZ
(2)m1和m2是非负整数,则m2|m1,当且仅当m1Z 属于m2Z
18、如何利用子群构造子群?写出两种利用子群构造新子群的方法
(1)H1和H2是阿贝尔群的子群,则H:= H1H2也是G的子群
(2)H1和H2是阿贝尔群的子群,则H:=H1交上H2也是G的子群
19、什么是正规子群?什么是商群?如果利用正规子群构造商群?
(1)设N是G的子群,对于所有a属于G,都有aN = Na ,称N为G的正规子群
(2)
阿贝尔群的子群都是正规子群
阿贝尔群的任意子群都可以构造商群
阿贝尔群构造的商群也是阿贝尔群
22、LFSR
23、如何判断一个群是子群?
24、在群中,拉格朗日定理指的是什么?

25、什么是广群?什么是半群?什么是幺半群?
广群:集合在预先定义的二元运算下满足集合内元素的 封闭性
半群:满足封闭性和结合律的群

26、什么是零元?请举例说明。什么又是零因子?请举例说明

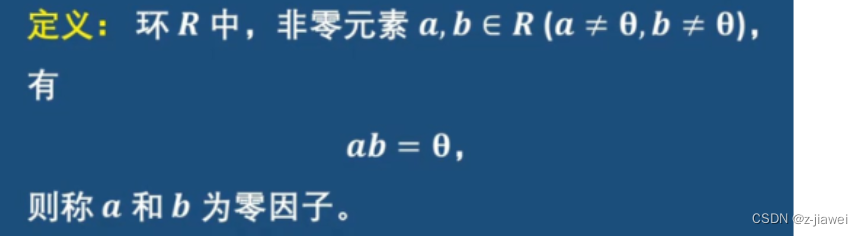
28、什么是算术基本定理?什么是欧几里得定理?
(1)、任何一个大于1的自然数N都可以被唯一地分解为有限个质数的乘积
(2)计算两个非负整数的最大公约数,两个整数的最大公约数等于其中较小的数和两数相除余数的最大公约数
29、
(1) -26 mod 11 (-26+33)mod 11 = 7
(2)3的负1次方 mod 7
1、改写n ≡ (1/3) (mod 7) 2、变换 3n ≡ 1 (mod 8) 3、此时再变换 3n mod 8 = 1,n取整
(3)3的2022次方 mod 8 可以尝试着从零开始,找规律
30、一个安全的公钥密码算法应该满足哪5个要求?
(1) 接收方B产生密钥对(PKb和SKb)在计算上是容易的
(2)发送方A对消息m加密产生密文c在计算上是容易的
(3)接收方B用自己的密钥对c解密在计算上是容易的
(4)敌手通过PKb球SKb在计算上是不可行的
(5)敌手由密文c和PKb恢复明文在计算上是不可行的
31、椭圆曲线加密算法的公私钥的制作过程是什么?
(1)选择一条椭圆曲线Ep(a,b),并取椭圆曲线上一点作为基点P
(2)选择一个大数K作为私钥,并生成公钥Q = k P
32、现有一个红球和绿球。某人想向你证明他不是色盲。请利用零知识证明协议,设计一个证明方法,在不告诉他球的颜色的情况下,证明他是否是色盲。写出具体的证明方法
证明者通过零知识证明向验证者证明某个声明,而不泄露其他消息
(1)、让这个人从两个盒子中随机选择一个盒子,每个盒子里都有一个球。一个盒子里的球是红色,另一个盒子里的球是绿色。如果这个人能够正确地选择出红球或绿球所在的盒子,那么他不是色盲;否则,他是色盲。
(准备阶段)验证者将两个盒子分别标记为A和B,红球放入盒子A,绿球放入盒子B,将盒子放在证明者面前
(声明阶段)假设它选择了盒子A,并向验证者声明我选择的是红球所在的盒子
(验证阶段)验证者打开这个人选择的盒子,确认球是红色的,并询问你确认红球是在这个盒子里面吗,证明者回答是,就说明不是色盲
33、现有明文 ilovechina。使用维吉尼亚密码进行加密。密钥是hbfu。加密的结果是什么?写出计算过程
和34解法相同
34、使用代换密码的思想对blockchain进行加密,密钥为like。写出加密过程。
blockchain ,like先写出每个字母在26个英文字母中出现的顺序,从零开始
根据密钥长度进行拆分,bloc kcha in 和 l i k e的顺序相加,得数对26取模就是最终结果
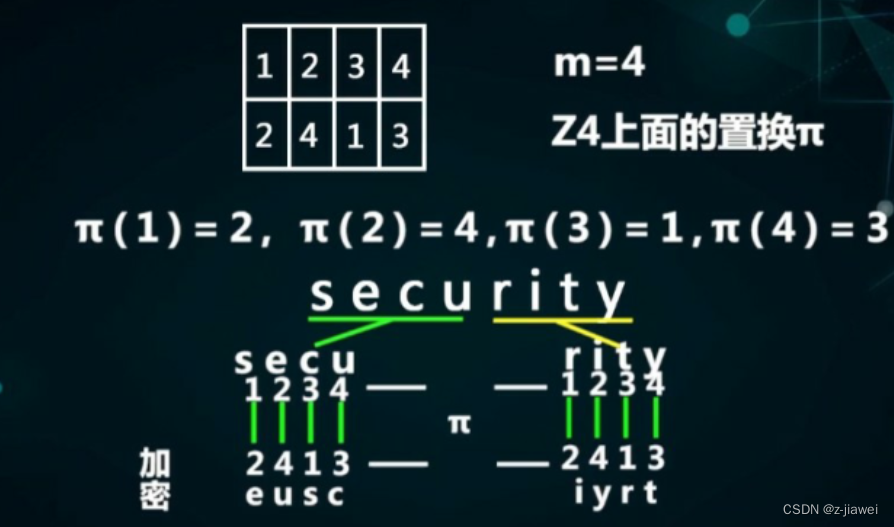
35、使用置换密码对blockchain进行加密。已知置换过程为:f(1) = 2, f(2) = 4, f(3) = 1, f(4) = 3。
置换密码:加密过程中不改变字母,只改变字母出现的位置和顺序
36、什么是平凡群?什么是非平凡群?
平凡群:只包含单位元e的群
非平凡群:不仅包含单位元e还包含其他元素的群
平凡子群:({e},x),(G,x)
非平凡子群:又叫真子群,(H,x),H不等于e,G
这篇关于密码学期末的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









