编程之美问题记录—

本文主要是介绍编程之美问题记录——数字之魅1，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

抽出一部分时间看了一点编程之美，思考的乐趣确实是一种享受。

求二进制中1的个数

分析：直接判断每一位，时间O(log2(n))。可以只判断”1”的个数。
$8_{10}=00001000_2$
只利用8本身来快速判断：它不是0，但是 00001000 & 00000111 = 00000000

int check(int n){int ans=0;while(n){ans++;n=n&(n-1);}return ans;
}

N!中末尾0的个数

（十进制中末尾0个数）
分析：这个问题可以转化成有多少个2和5的配对数。因为2的个数总是大于5的个数，即问题变成求解1——n中所有因子5的个数。
如30!，即是1——30的乘积，与5相关的数字有5,10,15,20,25,30，6个数字，同时25其实贡献了2个5，所以共有7个5。30/5=6. 6/5=1

int zero(int n){int ans=0;while(n){ans+=n/5;n/=5;}return ans;
}

求解N!二进制数字最低位1的位置。

（二进制中末尾0的个数）
分析：我们需要求出计算结果二进制形式的末尾0的个数，这和上面的问题联系在了一起，不过这次需要统计因子2的个数，有多少个2就提升多少位。但是书中给出了一种更加优秀的做法。 $h_{2的个数}=\frac{N}{2}+\frac{N}{4}+\frac{N}{8}+\frac{N}{16}+\cdots$
例如求解27!的二进制中最低位1的位置。

2710 = 110112 h = 1101 + 110 + 11 + 1 = (1000 + 100 + 00 + 1) + (100 + 10 + 0) + (10 + 1) + 1 = (1000 + 100 + 10 + 1) + (100 + 10 + 1) + 1 = 1111 + 111 + 1 = (10000 - 1) + (1000 - 1) + (10 - 1) + (1 - 1) [构 造] = 11011 - 1 的 个 数

$27_{10}=11011_{2} \\h=1101+110+11+1 \\=(1000+100+00+1)+(100+10+0)+(10+1)+1 \\=(1000+100+10+1)+(100+10+1)+1=1111+111+1=(10000-1)+(1000-1)+(10-1)+(1-1) \quad [ 构造 ] \\=11011-1的个数$
即n!末尾0的个数就是数字本身n-二进制中1的个数。

int two_zero(int n){int ans=0,old=n;while(n){ans++;n=n&(n-1);}return old-ans;
}

寻找最大的k个数

分析：可以用一个特别的数组装下最大的ｋ个数字，然后对于每一个新的数字判断它和其中最小值的关系，如果小弃之，大则替代最小值并更新这个数组。所以这个数组可以是最小堆，也可以是优先队列。

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
int g[1010];
void adjust(int p,int k){int q=p<<1;if(g[q]>g[q+1]) q++;if(q>k)  return ;if(g[p]>g[q]){int t=g[p];  g[p]=g[q];   g[q]=t;adjust(q,k);}
}
int main(){//freopen("cin.txt","r",stdin);int n,k;  // k<1010while(cin>>n>>k){for(int i=1;i<=k;i++) scanf("%d",&g[i]);sort(g+1,g+1+k);for(int i=k+1;i<=n;i++){int t;scanf("%d",&t);if(t>g[1]) {g[1]=t;adjust(1,k);}}for(int i=1;i<=k;i++){printf("%d ",g[i]); }puts("");}return 0;
}

最大公约数问题。

求解两个数的最大公约数
分析：传统的gcd()做法是

int  gcd(int a,int b){return b==0?a:gcd(b,a%b);
}

但是由于有取模的存在，有时会影响效率。
我们知道if (a,b)=c and a=p*a’, b%p!=0 then (a,b)=(a’,b)=c。　即可以取出不相关的部分。
那么，结合计算机的运算特点，可以进行左移和右移提取２。

#include <cstdio>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
bool odd(LL a){return a&1LL;
}
LL gcd(LL a,LL b){if(a>b) swap(a,b);if(a==1) return 1;if(a==0) return b;if(odd(a) and odd(b)) return gcd(a,b-a);if(!odd(a) and odd(b)) return gcd(a>>1,b);if(odd(a) and !odd(b)) return gcd(a,b>>1);if(!odd(a) and !odd(b)) return gcd(a>>1,b>>1)<<1;
}
int main(){LL a,b;while(cin>>a>>b){cout<<gcd(a,b)<<endl;}return 0;
}

计算斐波那契第n项值

快速计算的方式有:
1. 使用通项公式。
$F(n)=\frac{\sqrt{5}}{5}((\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n)$

最开始的几项值先递推计算出来并保存，后面n较大的情况可以使用此公式。
但是这种方法有浮点误差。
2. 矩阵快速幂，分治策略。
我们知道

(F (n) F (n - 1)) = (1110) (F (n - 1) F (n - 2))

$\begin{pmatrix}F(n) \\ F(n-1)\end{pmatrix}= \begin{pmatrix}1 & 1\\ 1 & 0 \end{pmatrix} \begin{pmatrix}F(n-1) \\ F(n-2)\end{pmatrix}$
所以，由此可以推算第n项。

快速寻找满足条件的两个数。

能否在一个数组里寻找两个数字，使得他们的和等于一个给定的数。
分析：将数组有序排列，比如从小到大。一个指针放左边，一个指针放右边，双方不断向中间移动，如果大了右指针左移，小了左指针右移。直到找到那个数字。

struct node{int p1, p2;node(int _p1,int _p2){  p1=_p1;  p2=_p2;  };
};
node myfind(int a[],int n,int sum){int i=0,j=n-1;while(i<j){if(a[i]+a[j]==sum) return node(i,j);else if(a[i]+a[j]>sum) j--;else i++;}return node(-1,-1);
}

有一个此问题的拓展应用：http://blog.csdn.net/thearcticocean/article/details/51055538

子数组的最大乘积。

计算长度是N的整数数组中任意N-1个数的组合中最大的一组。
分析：如果没有乘法计算溢出情况出现，可以直接先计算出所有数字的乘积然后针对第i个数字做除法分析即可。
如果存在乘法溢出的情况：
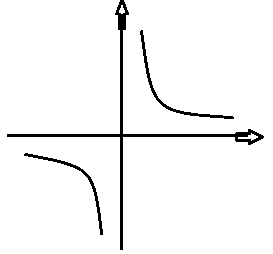
当所有数字的乘积b大于0，当前数字是a[i]–>x, 那么剩下的N-1个数字的乘积y=b/x，函数图像：
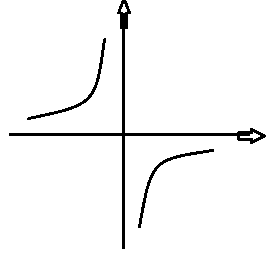
这里写图片描述
当b小于0,y=b/x函数图像：

还有b等于0的情况，如果数组中存在两个以上的0，那么y就等于0。如果仅仅存在一个0，那么我们可以统计正数和负数的个数分析得出结论。
所以，求解正数的个数，负数的个数，0的个数即可。

求解数组的子数组的最大和。

最大连续子序列问题。
分析：如果从前缀和考虑，那么时间复杂度是n^2
中间过程分析，每一个数字和前面数字的和要么相加要么不加，取最大的那种情况，不断更新答案。dp实现线性n的时间复杂度

int max_sum(int *a,int n){int ans=a[0],temp=a[0];for(int i=1;i<n;i++){temp=max(a[i],temp+a[i]);ans=max(ans,temp);}return ans;
}

子数组的最大和 - 二维

和上面的问题类似，但是二维（注意连续）。
分析：直接枚举计数的效果不理想。因为它和上面的问题有一定的相似性，可以借鉴上面的问题的解法。可以固定上下界然后就变成了一维子数组最大和的问题了。
这里写图片描述

code:

#include <iostream>
#include <cstdio>
using namespace std;
int g[6][6]={
1,-1,5,3,6,-2,
3,-2,7,8,-3,4,
4,2,1,6,-4,7,
5,2,1,0,1,1,
-2,5,3,1,-2,1,
1,2,-1,4,3,0
};
int h[6][6][6];  // h[j][r1][r2]第j列row1到row2的元素的和int main()
{for(int j=0;j<6;j++){for(int r1=0;r1<6;r1++){for(int r2=r1;r2<6;r2++){int temp=0;for(int r=r1;r<=r2;r++){temp+=g[r][j];}h[j][r1][r2]=temp;}}}int ans=-(1<<29);for(int r1=0;r1<6;r1++){   //dpfor(int r2=r1;r2<6;r2++){int temp=h[0][r1][r2];ans=max(ans,temp);for(int j=1;j<6;j++){temp=max(h[j][r1][r2],temp+h[j][r1][r2]);ans=max(ans,temp);}}}printf("%d\n",ans);ans=-(1<<29);for(int i1=0;i1<6;i1++){  // 暴力for(int j1=0;j1<6;j1++){for(int i2=i1;i2<6;i2++){for(int j2=j1;j2<6;j2++){int temp=0;for(int i=i1;i<=i2;i++){for(int j=j1;j<=j2;j++){temp+=g[i][j];}}ans=max(ans,temp);}}}}printf("%d\n",ans);return 0;
}