本文主要是介绍宽光谱SOA光芯片设计(二),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
-本文翻译自由Geoff H. Darling于 2003年撰写的文章。尽管文章较早,但可以了解一些SOA底层原理,并可看到早期SOA研究的思路和过程,于今仍有很高借鉴价值。
第3章 现代SOA设计基础
3.1简介
在本章中,将讨论现代SOA设计的关键问题。现有技术的基础将为后续章节的详细和专业研究提供必要的背景信息。
3.2 SOA的有源区设计
有源区决定了SOA的光学特性。它由波导结构内的增益介质组成。通常,使用体半导体或量子阱材料提供增益。对于波导结构,常见的有脊、埋肋和条形负载波导。所用波导的类型由可用的制造方法、使用的材料系以及SOA将与之匹配的输入和输出波导结构决定。
3.2.1增益介质:体半导体Vs量子阱
早期的激光器和SOA使用体半导体作为增益介质。直向双异质结构用来促进载流子在有源区内的复合。当体半导体变为单个和多个量子阱(MQW)时,性能显著改善[29]。量子阱增益介质可以允许更宽的光学带宽、更高的饱和输出功率、更低的透明电流密度、更大的限制因子以及对增益的偏振相关性的控制[30]。由于这些优势,MQW设计被用于光通信中的高性能激光器和SOA。本研究的主要焦点是MQW SOA的增益带宽特性。
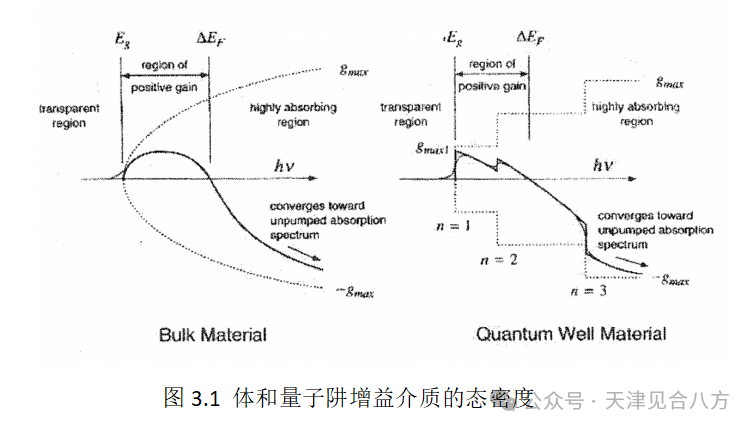
SOA的增益带宽表示光子能量的范围,光子能量可以激发比吸收跃迁(价带到导带)更多的辐射跃迁(导带到价带)。假设相似的载流子寿命,在给定的电流密度下,QW有源区更小,因此载流子密度更高。这导致准费米能级进一步渗透到导带和价带中。因此,在较大的光子频率范围内满足增益条件Eg<hυ<EFc-EFv[31]。另一个相关的论点是基于体材料和QW材料的态密度(DOS)结构,如图3.1所示。由于量子阱的阶梯形DOS小于任何光子能量的体值,在特定的载流子密度下,准费米能量必须更大,从而导致更宽的增益谱[31]。这些理论论证得到了实验结果的支持;体半导体通常提供45nm的增益带宽,而QW通常提供60-80nm[4,9]。
3.2.2量子阱设计
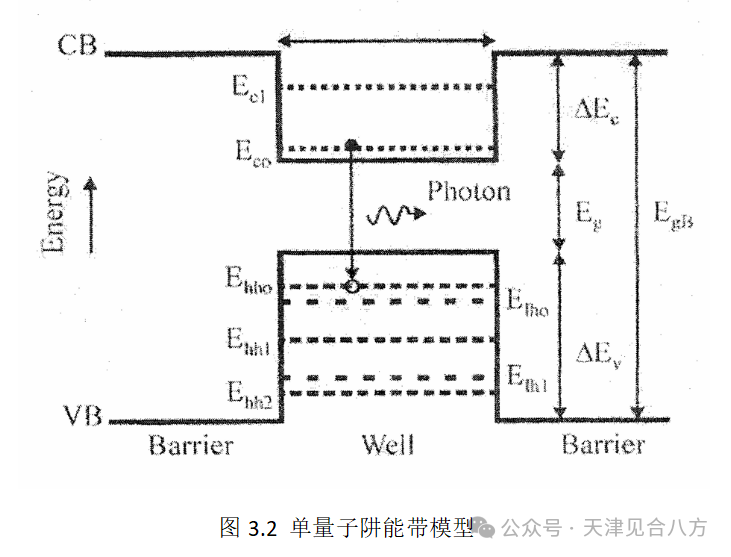
在设计量子阱SOA时,除了激光波长之外,还有许多因素需要考虑。阱的宽度和组成对整体器件性能至关重要。阱中足够的载流子限制和子带之间足够的间距之间的平衡也非常重要的。理想的QW将具有在子带之间具有大能量间隔的深度受限状态,以确保载流子在典型操作条件下仅限于第一状态。InGaAsP材料系统中的最佳阱宽度在5至10nm范围内[29]。如果来自第二导通子带的转变有贡献,则QW结构的增益带宽可以被扩展。已经使用这种方法制造了宽调谐的外腔MQW激光器,以提供超过200 nm的调谐范围[32,33]。这种带宽的提高是以整体器件性能的下降为代价的,因为注入的载流子现在必须保持或用于从两个导带状态转换的反转。典型的QW在导带中表现出一或两个束缚态,并且设计了足够的子带间距以确保从第一状态的转变占主导地位。图3.2展示了量子阱的能量结构。
量子阱的价带结构对整体性能有着重要的影响。有三个价带:一个轻空穴(LH),一个重空穴(HH),以及一个被称为分裂带的第三价带。分裂带位于价带深处,跃迁到它的可能性很小,因此在典型的操作条件下可以安全地忽略它的存在。LH和HH带的最大值出现在k空间的一个公共点,如图3.3所示。LH和HH带的作用将在下一节中进行更详细的讨论。
3.2.3偏振无关
现代光网络中的偏振态在相对较短的时间上连续波动。网络模块,包括SOA,必须被设计为平等地对待每个偏振状态。大量的学术和工业努力一直致力于设计与偏振无关的SOA。在本节中,讨论了SOA中偏振相关性的起源,并回顾了将其最小化的技术。
波导结构和增益介质本身都都会影响SOA的偏振相关性。两个横向维度的波导结构的差异改变了TE和TM偏振波的有效限制因子。由于每单位长度的光学增益是由限制因子线性缩放的,因此净TE和TM增益可能相差很大。按照惯例,TE模式具有平行于器件平面并平行于QW平面的电场矢量,而TM模式电场垂直于这些平面。体半导体相对于电场各向同性地提供增益。然而,TE和TM限制因子的差异改变了能够在体有源区中经历增益的每个模式的分数。首个偏振不敏感SOA器件在波导结构中使用了TE和TM平衡限制因子的体增益介质[34],实现了在以1.54um中心波长的45nm的3dB带宽范围内,TE和TM的增益偏差在1dB内。
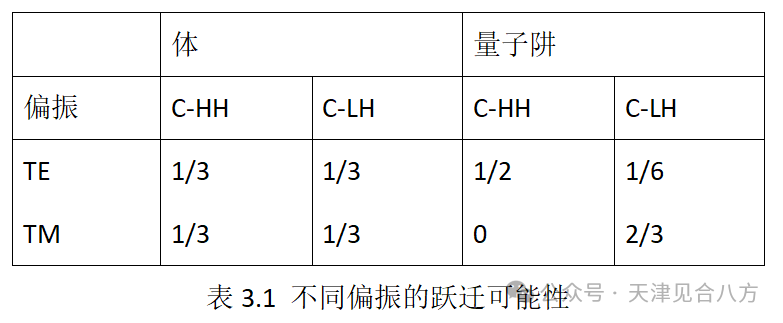
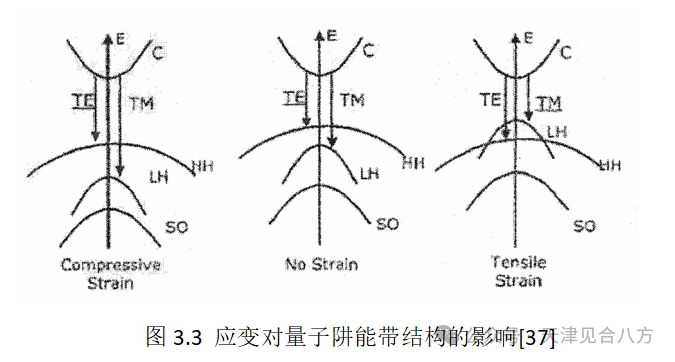
在MQW结构中,量子约束打破了LH和HH带的简并性,并改变了导带跃迁的可能性。LH和HH波段的跃迁与电磁波的特定极化相互作用最强烈。这些相互作用的比率如表3.1所示,由动量矩阵自变量确定[35]。TE光将与HH带强烈相互作用,而TM光主要与LH带相互作用。在晶格匹配的MQW结构中,HH带位于价带的顶部,最容易填充。因此,在晶格匹配器件中,TE模增益通常超过TM模5-10 dB[36]。将应变引入量子阱改变了LH和HH带的相对能量。通过调整阱和势垒的组成来引入应变,以在晶格常数中产生小的失配。无缺陷、应变阱和势垒可以生长到临界厚度,在临界厚度处,缺陷、浓度开始损害性能。幸运的是,临界厚度是几十纳米,并且超过了QW有源区中使用的层厚度。拉伸应变提高了LH带的能量,因此TM增益增加。压缩应变具有相反的效果,并增加TE增益。这些影响如图3.3所示。
Magari等人[38,39]通过应变拉伸量子阱设计了偏振无关SOA,在200 mA的驱动电流下获得了27.5 dB的最大增益。然而,在一般情况下,TE和TM模式的光谱增益曲线的形状随着驱动电流的变化而变化。此外,没有提供详细的3dB光谱宽度测量结果,以及TE/TM增益合理平衡的驱动电流范围。通常,拉伸应变仅在有限的驱动电流范围内用于平衡TE/TM增益。在整个驱动电流范围内平衡增益是不现实的。在实践中,由于1550nm附近的InGaAsP中的晶格常数和带隙约束,很难独立地选择中心波长和水平拉伸应变。
Mathur等人在电流无关的偏振无关SOA设计方面取得了重要进展。他们将3个压缩应变量子阱和3个拉伸应变量子阱合并到单个有源区中。通过控制器件长度和驱动电流的特定组合,实现了1300 nm偏振无关SOA[40]。不久之后,Tiemeijer等人对设计进行了改进,以在更大参数范围内提供增益均衡。他们的设计使用了三个1%拉伸应变的110Å阱和四个1%压缩应变的45Å阱。对于25至200 mA的驱动电流,TE/TM增益偏差控制在1 dB以内,1300nm下的3dB光谱宽度约为30-40 nm[41]。Newkirk等人在1500 nm处成功应用了相同的方法。其中实现了大约100 nm的3dB增益带宽[42]。近年来,[37,43]也报道了类似的工作。
1996年,J.J.He等人使用QWI来平衡MQW SOA器件中的TE和TM增益[26]。混合引起阱和势垒组合的变化以改变LH和HH能带。发现在特定注入水平下,从生长状态的40nm蓝移均衡了TE和TM增益。
3.2.4串扰最小化:增益箝位
理想的放大器提供与输入功率无关的恒定增益。由于下面关系式所描述的饱和效应,实际SOA的运行与理想相差甚远:

其中Ps是饱和输出光功率,增益下降50%时的输出功率,Pin是总输入功率。饱和度对于Pin<<Ps来说是不重要的,但随着Pin接近Ps,饱和度变得越来越重要。此外,输入功率是指增益谱中所有波长的总输入功率。当多个波长通过SOA时,这可能会导致串扰。如果一个波长的功率上升(下降),则当功率的变化发生在小于增益介质的恢复时间的时间尺度上时,其他波长所经历的增益将下降(上升)。SOA中的载波响应时间大约为数百皮秒。Pin的变化如果在比这更快将影响增益,直到载波能够恢复。因此,在调幅WDM应用中,一个信号的比特模式可以影响其他信号的增益,导致串扰。
增益箝位技术已被设计用于管理SOA中的串扰效应[2,3]。这些技术通过在带外的一个固定波长下向SOA提供光学反馈,该波长将根据反馈控制载波密度以及增益。与以反馈波长振荡的大量功率相比,输入信号中的后续波动较小,因此g(w)不受影响。已经开发了几种用于在箝位波长下提供反馈的巧妙几何形状,包括正交VCSEL方法和分布式布拉格反射器(DBR)的使用。
3.3. 腔体设计
3.3.1波导
光信号在SOA中传播时需要横向限制。它们应该被限制在单模,以确保与有源区的稳定重叠,并简化与单模光纤的耦合。通常在III-V半导体芯片中使用脊形波导。在这些情况下,通过生长很有效折射率高于上包层和下包层的有源区来提供强的垂直约束层的相对厚度和折射率决定了单模条件。在水平维度上,弱约束由晶片表面上、上包层上方的蚀刻脊提供。脊尺寸的适当选择充分地将光学模式限制在横向尺寸上。
3.3.2耦合效率
在SOA中,光从单模光纤(SMF)耦合到半导体波导,然后返回光纤。高效耦合通过提高总增益和降低放大器的噪声系数来提高SOA性能。噪声系数由其nsp/Ci(总体反转因子除以输入耦合效率)给出,噪声系数限制了网络中可以级联的放大器数量。SOA和EDFA常见的噪声系数为6-10dB和3-6dB[4,44]。
SOA芯片与光纤的耦合效率由每个波导的模式的重叠积分决定。单模光纤具有平均场直径(MFD)为10um的圆形轮廓。许多光电子波导器件,包括本工作中使用的结构,具有1/2x2um量级的椭圆模斑,导致模式尺寸和形状失配。
需要对焦来补偿模式大小失配。这可以用微光学元件来实现,尽管通过锥形光纤或在光纤端面抛光形成透镜光纤通常更方便。锥形透镜光纤(TLF)可在市场上买到,其光斑尺寸小至3um,工作距离为5至50um。光电子器件的小模尺寸需要亚微米精度的XYZ三维调节来将TLF对准波导面。尽管TLF将光纤模式聚焦到波导面上,但它们不能补偿波导模式的椭圆度。已经开发出将称为锥形的无源波导部分与SOA和激光器集成的技术。在锥形波导中,模式尺寸和形状随着波导尺寸的缓慢变化而变化,横向和垂直锥形均有使用以确保在每个设备端面的模式匹配。有关III-V族半导体中锥形设计的详细讨论,请参阅[45]。由于封装成本在SOA的总成本中占主导地位,因此开发用于简化光纤和SOA之间耦合的集成解决方案将带来显著的竞争优势。将锥形集成到SOA设备中增加了设计和制造步骤的复杂性,但大大简化了与光纤的耦合,降低了封装的成本。
3.3.3反射抑制
来自SOA端残余反射在增益谱中引起不期望的法布里-珀罗谐振,进而带来增益纹波,这使得波分复用光网络中的部署复杂化。因此,必须采取措施对每个半导体空气端面处的反射率降低30%。抗反射(AR)涂层和斜切是现代SOA中用于反射抑制的两种主要技术。利用AR涂层,当具有适当厚度和折射率的介电材料层沉积到器件面上时,形成干涉滤光片。适当设计的多层AR涂层可以在40 nm的带宽上将反射率降低到10-3以下[30]。AR涂层对于降低输入耦合损耗同样重要,这反过来又改善了放大器噪声系数。Zah等人在1987年首次采用了斜切,其波导面端面不垂直[46]。典型的倾斜角度范围从4度到14度不等,与偏振无关,可以在大波长范围内将反射率降低10-4以下。随着倾角的增加,远场不对称性开始降低与光纤的耦合效率。因此,最佳倾斜角度在7-10度之间[30]。在工业上,将斜切和AR涂层相结合是有利的。这降低了涂层公差,同时仍然确保了10-5量级的可接受的低反射率,这足以将增益波纹保持在1dB以下。
第4章 宽光谱SOA设计
4.1简介
上一章我们探讨了现代SOA设计理论。本章我们聚焦到如何通过将量子阱混合技术应用于双段SOA上来提高增益带宽。在本章中,介绍了一种新型SOA结构,并介绍了用于制作原型器件的生长和处理技术,随后分析了波导结构的导波特性,最后介绍并设计了MQW SOA的增益光谱模型,以提供对器件性能的定性分析。
4.2双段SOA结构
本项目的SOA结构是基于在InGaAsP材料系中生长的3量子阱脊波导结构。图4.1展示了两张原子力显微镜(AFM)图像,脊、漏极区域和接触焊盘清晰可见。脊波导器件依赖于电流从接触焊盘流过漏极区,向上流过脊壁,然后向下穿过脊的顶部进入有源区。为了描绘两个电无关的段,在器件两段之间引入金属化和上接触层中的5um分割。这种分割如图4.1和4.2所示。
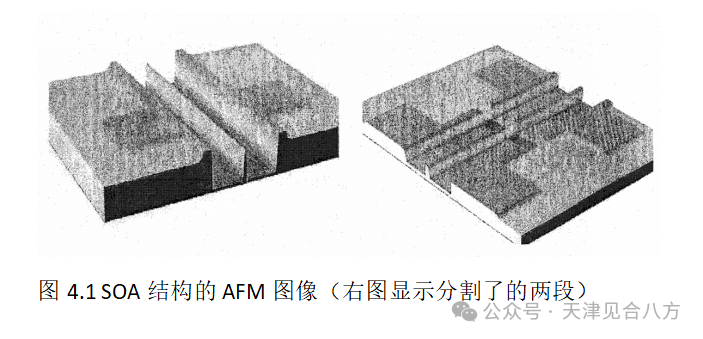
作为本研究起点的底层脊波导和多量子阱(MQW)设计最初是由麦克马斯特的合作者为DFB激光应用设计的。因此,该设计高度依赖于偏振。由于本项目的主要目标是最大限度地提高整体增益和发射带宽,时间限制没有为了优化偏振特性进行彻底修改。然而,在最后的制造过程中,对MQW设计进行了些修改,以提高偏振无关特性。

4.3生长过程:分子束外延(MBE)
利用分子束外延(MBE)技术在n掺杂InP衬底上生长器件。表4.1给出了从顶部(脊波导,p接触层)到底部(n侧衬底)的每一层的特性。相对于其他外延技术,如液相或化学气相沉积,分子数外延MBE允许在精确控制成分的情况下直接沉积原子级薄层。其特点是在600至800°C的温度范围内生长速率低。
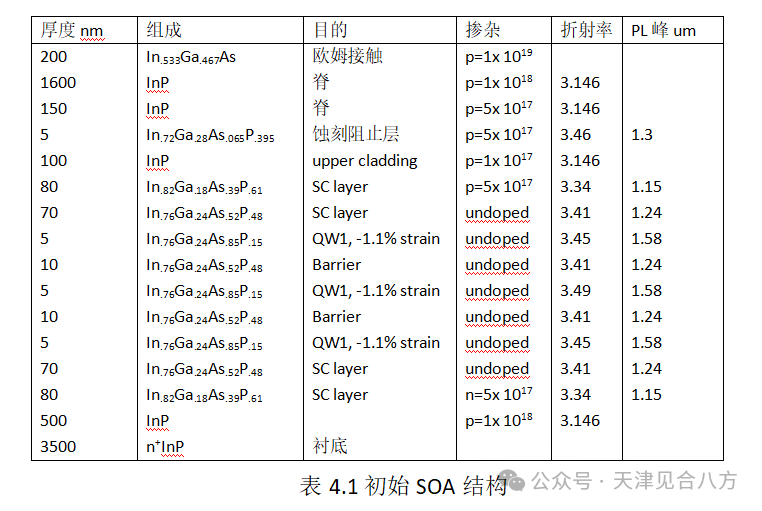
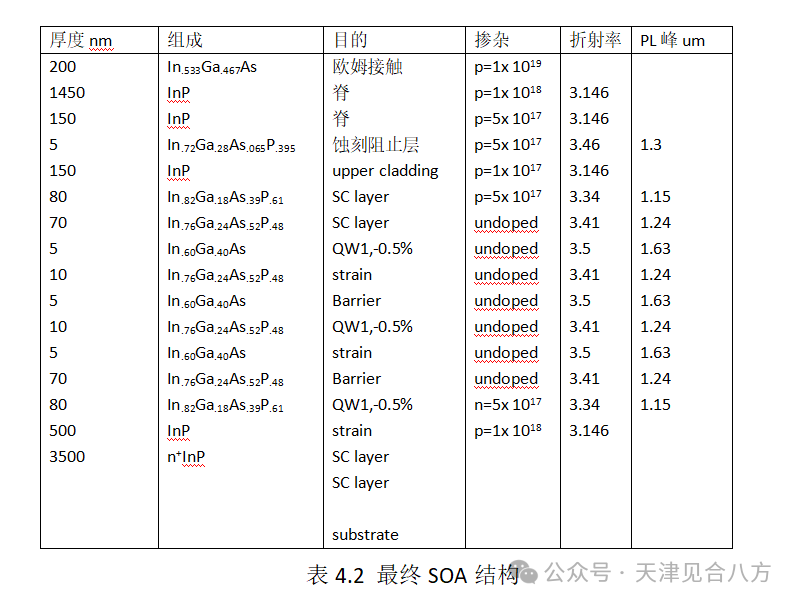
初始SOA结构的每一层都与InP衬底晶格匹配,但三个量子阱除外,它们处于大约1.1%的压缩应变下。如第3章所述,这种类型的应变增强了QW有源区中的TE增益。由于晶格常数和带隙能量约束相互冲突,在InGaAsP材料系统中很难设计和生长在1500-1600nm光谱的拉伸应变量子阱。在最后一轮制造中,对QW进行了调整,减轻一些压缩应变,最终的SOA结构包含在表4.2中。
4.4量子阱混合过程
QWI用于引入两个SOA段的增益谱之间的相对蓝移。该技术基于无杂质空位扩散(IFVD),其中来自沉积在选定区域上的覆盖层的空位扩散到QW区域,并促进III族原子从QW向外扩散,从而增加有效跃迁能[20]。使用Fick第二扩散定律[47,48]对QWI过程进行了充分建模,如方程4.1,由扩散系数D、退火时间t、量子阱厚度Lz和扩散的初始浓度X0[48,49]决定。
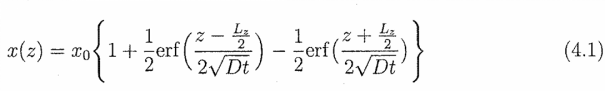
混合过程在概念上如图4.3所示。方程4.1被广泛接受,并通过实验证实适用于AlGaAs/GaAs QW结构。实验结果似乎表明,该模型不适用于InGaAs/InP结构中 [50]。Mukai等人研究了这种材料系的扩散过程,并开发了一个更复杂的模型,该模型考虑了晶格畸变效应,并且不假设层界面上的成分是连续的[51]。
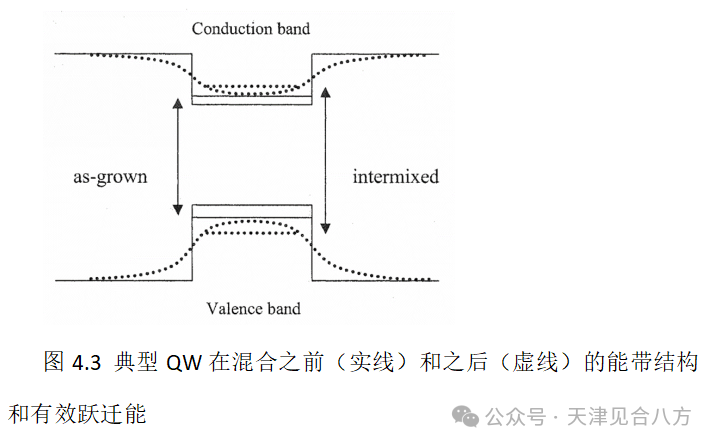
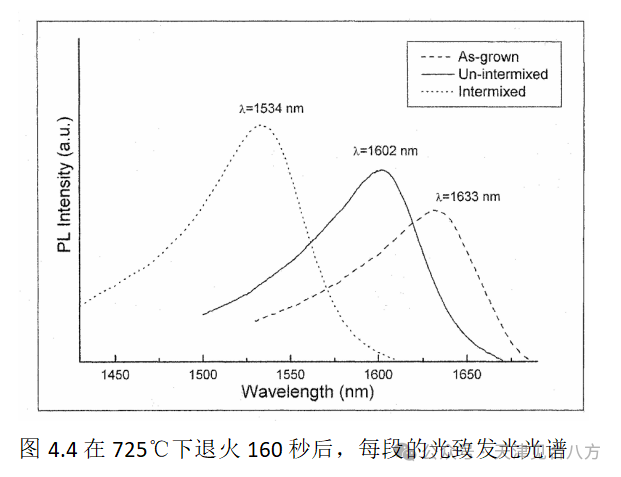
在用MBE沉积表4.1中的每一层之后,在器件的每段上生长专有的覆盖层[21]。当覆盖层生长在200nm厚的接触层之上并且其间具有小的牺牲层以保护接触层时,实现了可再现的混合。在覆盖层就位的情况下,整个晶片经历快速热退火(RTA)。RTA包括在700至800°C的温度下持续数十秒。蓝移的量随着RTA温度和持续时间的增加而增加。在RTA期间,由于在升高的温度下增加的扩散常数,没有覆盖层的晶片区域经历了少量的混合。这是可以管理的,因为关键的设计参数是SOA部分之间的相对蓝移,可以高度准确地进行控制。校准试验的样品光致发光信号如图4.4所示。使用带有HeNe激光器和锁定放大器的1nm分辨率单色仪在室温下测试。该图显示了器件的生长态、未混合区和混合区的PL光谱。每个晶片的一部分用于校准作为退火温度和持续时间的函数的器件部分之间的相对蓝移。
在RTA步骤之后,蚀刻掉覆盖层,并且用两步蚀刻工艺限定上部波导结构。使用反应离子蚀刻(RIE)来制作脊波导的垂直壁。对于RIE,蚀刻速率具有与其相关的不确定性,并且InP和InGaAsP都受到影响。为了避免蚀刻过深到超过5nm蚀刻阻止层的结构中,RIE步骤提前停止。然后使用湿法蚀刻来限定脊波导的下部,这种蚀刻技术沿着InP晶面进行,但对四元InGaAsP没有影响,湿法蚀刻在5nm蚀刻阻止层处自动停止。
随着脊波导结构的完成,在漏极区上并沿着脊壁沉积绝缘氧化物层。金属化产生了从每个脊的顶部、沿着脊壁、穿过漏极区到接触焊盘的连续金属接触。在接触到位的情况下,将晶片切割成条状进行测试。为了抑制反射,将器件与衬底的切割平面成7度角生长。
4.5波导特性研究
SOA结构基于脊波导设计如图4.1所示。Selene是Kyamata软件公司的一种商用光学仿真工具,用于研究2、3和4um宽脊波导的传输特性。为了仿真,将每层的厚度、宽度和折射率一起输入到软件包中,完整输入参数后,将有限差分算法部署在用户定义的计算网格上。为了确保结果准确,网格大小设置为小于材料中波长的10%。
4.5.1模态分布估计
波导结构的有限差分仿真提供了每个偏振模式的特征模式分布。在有源区中心周围的10×8um区域上部署了一个300×300的计算网格。这种配置在几分钟的计算后提供了准确的结果,并且加倍的网格密度使特征场尺寸变化小于1%。为了简化后续建模,对所得模式剖面进行二维高斯拟合,其形式如下:
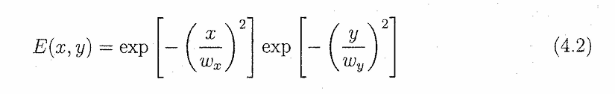
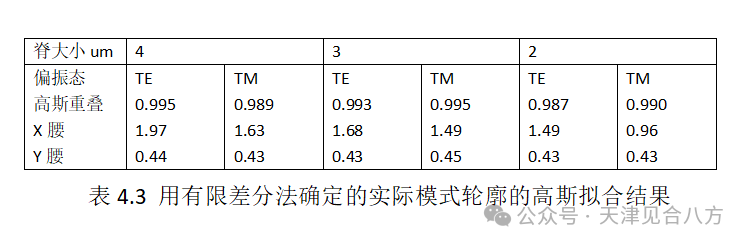
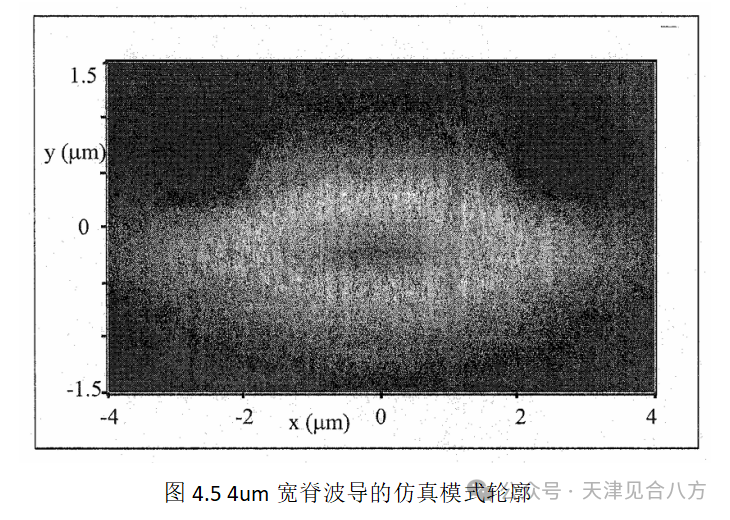
其中Wx和Wy是每个横向维度中的高斯束腰。表4.3总结了这些拟合的结果。接近1的重叠因子证实了2D高斯拟合是对实际器件模式的良好近似。图4.5显示了4um脊波导的仿真模式。
4.5.2限制因子估算
限制因子Γ表示导模电场与有源区体积重叠的部分。它以指数函数调节材料增益和器件长度,以产生器件的单程增益。限制因子等于横向和纵向因子Γxy和Γz的乘积。对于面内激光器,其中腔比辐射波长长得多,有源区延伸了腔的长度,此时纵向因子约等于1。可将限制因子简化为:[29]
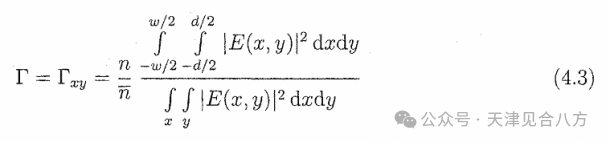
方程4.3定义了横向面积为w×d的有源区的限制因子和电场E(x,y)。是有源区的折射率与模式的有效折射率的比值,并且近似为一[52]。
使用表4.3中的TE和TM高斯拟合参数计算每个阱的TE和TM限制因子。这些结果包括在表4.4中。

4.5.3. 反射抑制
如第3章所述,反射抑制是SOA设计的一个重要方面。端面反射会导致增益谱中的法布里-珀罗谐振,为了最大限度地减少这种反射,将抗反射涂层与斜波导相结合,以抑制反射。抗反射涂层能力不适用于本次研究。使用一维模型可获得有效面反射率的估计值,该模型校正了端面导波的角菲涅耳反射率[53]。
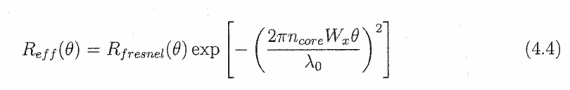

在过去几年中,已经收敛到7-10度,作为抑制反射的最佳值[26,37,43]。波前不对称性随着倾斜角度的增加而增加,并降低与光纤的耦合效率。我们选择了7度倾斜角,以在不影响耦合效率的情况下提供足够的反射抑制。
4.6 SOA增益的稳态建模
本节的目标是通过建模深入了解MQW SOA结构的光谱增益特性。探索了一系列设计参数,以阐明器件增益带宽的趋势。在介绍了半导体中的增益建模之后,讨论了建模应变量子阱的细微差别,最终从文献中提取了一个合适的模型。软件被配置为接受一系列设计参数,如阱和势垒成分、层厚度等。所得的光谱增益函数用于估计MQW SOA的单程增益。
4.6.1增益建模技术综述
体半导体增益
体半导体增益特性建模的分析需要能带和价带能作为波矢量的函数。计算能带结构的方法复杂、耗时[54]。幸运的是,带边缘附近的带结构区域通常主导光学增益响应,并且存在许多用于计算这些区域中的带结构的近似技术。大多数技术都基于理论,并涉及对特定波矢量值的能带结构的二次近似,通常是直接间隙半导体中的k=0能带边缘[35]。通过引入与抛物线带曲率成反比的电子和空穴有效质量的概念,可以定性和定量地了解带结构对增益特性的影响。
理论的全部复杂性不需要使用抛物带近似来仿真体半导体中的增益过程。为了部署基于抛物线带近似的精确增益模型,需要研究中材料系的有效质量值,并且通过实验获得[55]。在研究量子阱结构时,需要对理论进行重新定义。这些改进是基于Kane[56]和Luttinger-Kohn[57]的模型,分别考虑了自旋轨道相互作用和简并带[35]。除了理论之外,量子阱激光器的宏观分析近似也得到了发展。Balle开发了量子阱光学易感性的简化分析表达式,再现了更复杂模型的许多定性结果[58]。同样,Makino使用抛物带近似[59]开发了量子阱激光器增益特性的近似分析公式。为了简化计算,Makino使用了Asada等人的跃迁加宽模型。[60]
量子阱中应变的存在显著改变了导带和价带结构,使许多理论方法失效。然而李等人证明,只要使用应变校正的有效质量,抛物线带模型就可以很好地近似应变量子阱[61]。
当对任何事物建模时,需要在准确性和易用性之间进行平衡。在使用抛物线带模型时,认识到其局限性是很重要的。在假设E-k图是各向同性的情况下(如通过用其标量大小替换波矢量),E-k图中的任何潜在各向异性都被忽略。这一假设的有效性在很大程度上取决于物质系统。在GaAs中,已知重空穴带是高度各向异性的,这降低了这一假设的有效性。然而,在未应变的InGaAsP量子阱中,Zielinski等人使用各向同性假设对量子阱器件进行建模,并与实验测量结果非常一致[62]。随着实际频带曲率变得越来越非抛物线,抛物线带模型的有效性在带边缘进一步降低,这限制了增益谱的准确性。
为了对量子阱参数在确定光谱增益特性中所起作用的定性分析,选择了Makino的模型是因为其相对易于实现。
4.6.2应变量子阱QW增益建模
在本节中,给出了Makino抛物带模型的一个简明推导。与所研究结构相对应的一系列材料参数是从参考文献中以表格形式汇编而成的。
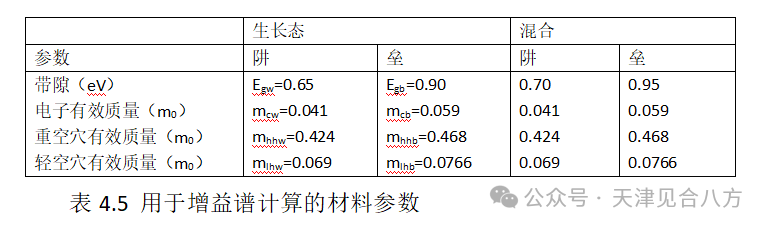
创建该模型的第一步是从阱和势垒的四元成分中插值获得必要的材料参数。带隙能量和有效质量如表4.5所示,分别使用[35,55]和[61]中的InGaAsP插值公式计算。
在确定相关材料参数后,使用抛物线带模型计算QW的第一导带以及第一轻空穴和重空穴价带的子带能级。QW的能量结构,包括导带和价带子带能级,如图4.6[30]所示。

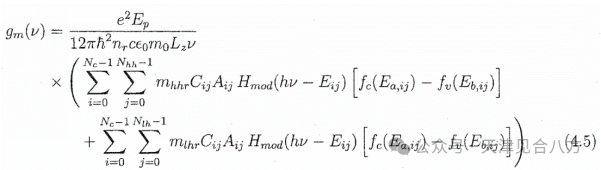

使用Matlab进行增益谱计算。首先使用超越求解方法计算子带能级,然后计算了一系列载流子密度的准费米能级。这些计算包括导带中的第一束缚态和价带中的重空穴和轻空穴的第一束缚状态。来自第二束缚态的贡献很小,可忽略。准费米能级用于计算作为方程4.5中使用的光子能量函数的占据概率。图4.7显示了表4.5中两种不同QW结构的样品TE增益谱。
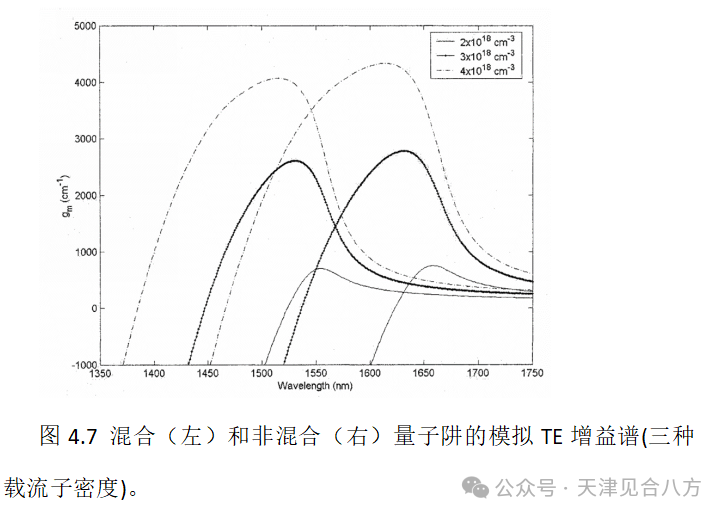
QWI对增益谱的影响
QWI过程在每个段之间引入特定量的相对蓝移。在退火过程中,两个段都经历了光致发光效率的增加以及光谱蓝移,尽管覆盖部分经历了更大的蓝移,如图4.4所示。混合后QW的有效子带能级的分析模型是复杂和近似的。这些模型在InGaAsP中变得越来越复杂,其中III族和V族元素的扩散可以以不同的比例发生,这取决于混合技术[50,51,63]。此外,用于这项工作的QW结构中应变的存在引入了复杂性。
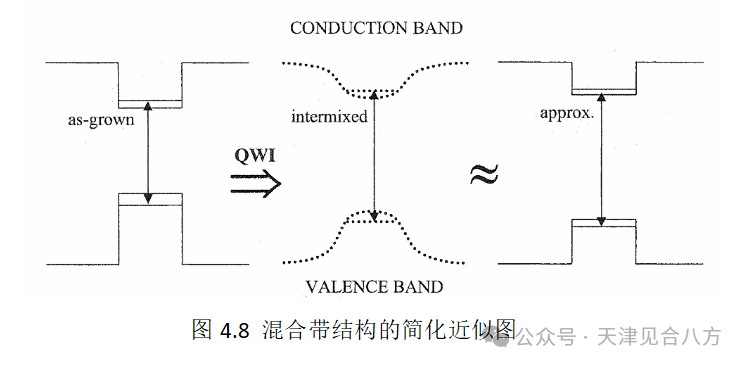
为了定性分析,复杂的模型是不适合的。为了便于计算,使用了图4.8所示的混合简化模型。对于该模型,增加阱的带隙能量以引起跃迁能量的适当蓝移,从而定性地近似于混合的影响。该模型没有考虑带结构和混合引起的应变的变化。因此,增益谱的偏振和载流子依赖性将不是完全准确的。
QW增益模型的应用
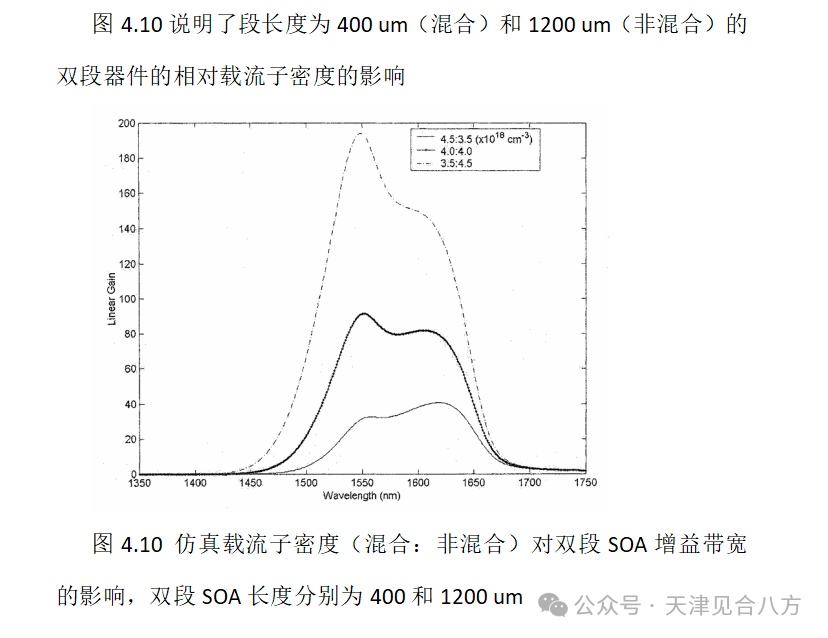
在本节中,图4.7中所示的QW增益谱应用于两段MQW SOA设计,以研究段相对长度和注入水平对整体增益带宽的影响。这些预测适用于小信号、连续波操作;不包括串扰和饱和效应。方程4.6给出了作为波长和载流子密度函数的双段SOA的稳态小信号单程增益
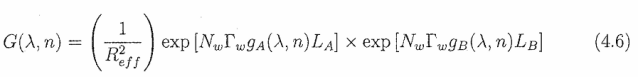

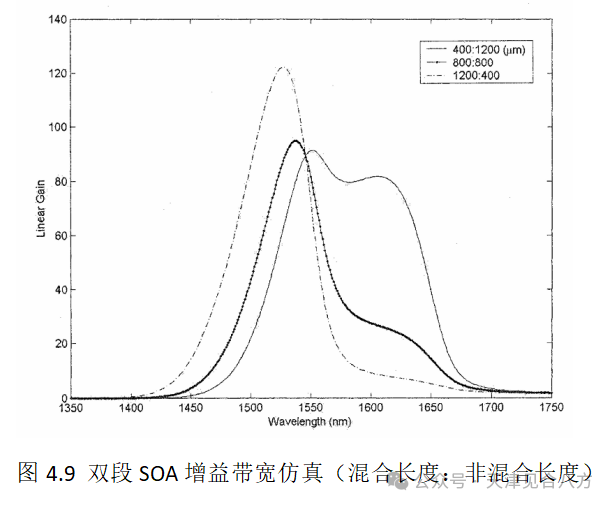
图4.9说明了相对段长度对光谱增益特性的影响。在这个例子中,对于具有3个量子阱的1600um长的双段SOA段长比(混合:未混合)是变化的。每段的载流子密度为4×1024cm-3。
[28] P. Poole, V. M. Davies, M. Dion, Y. Feng, S. Charbonneau, R. D. Goldberg, and I. V. Mitchell, “The fabrication of a broad-spectrum light emitting diode using high energy ion implantation,” IEEE Photon. Technol. Lett., vol. 8, pp. 1145-1147, 1996.
[29] L. A. Coldren and S$. W. Corzine, Diode Lasers, and Photonic Integrated Circuits. New York: John Wiley and Sons, Inc., 1995.
[30] M. J. Connelly, Semiconductor Optical Amplifiers. Boston: Kluwer Academic Publishers, 2002.
[31] T. R. Chen, L. Eng, Y. H. Zhuang, and A. Yariv, “Quantum well super luminescent diode with very wide emission spectrum,” Appl. Phys. Lett., vol. 56, pp. 1345-1346, April 1990.
[32] D. Mehuys, M. Mittelstein, A. Yariv, R. Sarfaty, and J. E. Ungar, “Optimized fabry perot (AlGa)As quantum-well lasers tunable over 105 nm.,” Electron. Lett., vol. 25, pp. H. 143-145, 1989.
[33] H. Tabuchi and H. Ishikawa, “External grating tunable MQW laser with wide tuning range of 240 nm,” Electron. Lett., vol. 26, pp. 742-743, 1990.
[34] B. Mersali, G. Gelly, A. Accard, J. L. Labfragette, P. Doussiere, M. Lambert, and Fernier, “1.55 micron high-gain polarization-insensitive semiconductor travelling wave amplifier with low driving current,” Electron. Lett., vol. 26, pp. 124-125, Jan. 1990.
[35] S. L. Chuang, Physics of Optoelectronic Devices. New York: John Wiley and Sons, 1995.
[36] M. Joma, H. Horikawa, C. Zu, K. Yamada, Y. Katoh, and T. Kamijoh, “Polarization insensitive semiconductor laser amplifiers with tensile strained InGaAsP /InGaAsP multiple quantum well structure,” Appl. Phys. Lett., vol. 62, pp. 121-122, Jan. 1993.
[37] P. Koonath, S. Kim, W.-J. Cho, and A. Gopinath, quantum-well semiconductor optical amplifiers,” IEEE J. Quantum Electron., vol. 38, pp. 1282-1290, Sept. 2002.
[38] K.Magari, M. Okamoto, H. Yasaka, K. Sato, Y. Noguchi, and O. Mikami, “Polarization insensitive travelling wave type amplifier using strained multiple quantum well structure,” IEEE Photon. Technol. Lett., vol. 2, pp. 556-558, Aug. 1990
[39] K. Magari, M. Okamoto, and Y. Noguchi, “1.55 micron polarization-insensitive high gain tensile-strained-barrier MQW optical amplifier,” IEEE Photon. Technol. Lett., vol. 3, pp. 998-1000, Nov. 1991.
[40] A. Mathur and P. D. Dapkus, “Polarization insensitive strained quantum well gain medium for lasers and optical amplifiers,” Appl. Phys. Lett., vol. 61, pp. 2845-2847, Dec. 1992
[41] L. Tiemeijer, P. Thijs, T. van Dongen, R. Slootweg, J. van der Heijden, J. Binsma, and M. Krijn, “Polarization-insensitive multiple quantum well laser amplifiers for the 1300 nm window,” Appl. Phys. Lett., vol. 62, pp. 826-828, Feb. 1993.
[42] M. Newkirk, B. Miller, U. Koren, M. Young, M. Chien, R. Jopson, and C. Burus, “1.5 micron multi-quantum-well semiconductor optical amplifier with tensile and compressively strained wells for polarization-independent gain,” IEEE Photon. Technol. Lett., vol. 4, pp. 406-408, Apr. 1993.
[43] M. Silver, A. Phillips, A. Adams, P. Greene, and A. Collar, “Design and ASE characteristics of 1550nm polarization-insensitive semiconductor optical amplifiers containing tensile and compressive wells,” IEEE J. Quantum Electron., vol. 36, pp. 118-122, Jan. 2000
[44] J. J. Bernard and M. Renaud, “Semiconductor optical amplifiers,” OE Magazine, Sept. 2001.
[45] I. Moerman, P. P. V. Daele, and P. M. Demeester, “A review on fabrication technologies for the monolithic integration of tapers with ITI-V semiconductor devices,” IEEE J. Select. Quantum Electron., vol. 3, Dec. 1997.
[46] C. E. Zah, J. S. Osinski, C. Caneau, S. Menocal, L. Reith, J. Salzman, F. Shokoohi, and T. Lee, “Fabrication and performance of 1.5um InGaAsP travelling-wave laser amplifiers with angled facets,” Electron. Lett., vol. 23, pp. 990-992, 1987
[47] J. Crank, Mathematics of Diffusion. England: Oxford University, 1957.
[48] J.-C, Lee and T. E. Schlesinger,” Interdiffusion of Al and Ga in (Al,Ga)As/GaAs superlattices,” J. Vac. Sci. Technol. B, vol. 5, pp. 1187-1190, July/August 1987.
[49] L. L. Chang and A. Koma, “Interdiffusion between GaAs and AlAs,” Appl. Phys. Lett., vol. 29, pp. 138-141, Aug. 1976.
[50] E. H. Li, ed., Semiconductor Quantum Wells Intermixing: material properties and optoelectronic applications, vol. 8 of Optoelectronic Properties of Semiconductors and Superlattices. Gordon and Breach, 2000.
[51] K. Mukai, M. Sugawara, and S. Yamazaki, “Interdiffusion process in lattice-matched InxGa1-xAsyP1-y/InP and GaAs/AlxGa1-x,As quantum wells,” Phys. Rev. B, vol.50, pp. 2273-2282, July 1994.
[52] G. P. Agrawal, Fiber-Optic Communication Systems. New York: John Wiley and Sons, Inc., second ed., 1997.
[53] D. Marcuse, “Reflection loss of laser mode from titled end mirror,” IEEE J. Lightwave Technol., vol. 7, pp. 336-339, Feb 1989.
[54] N. W. Ashcroft and N. D. Mermin, Solid State Physics. New York: Harcourt Brace College Publishers, 1976.
[55] S. Adachi, Physical Properties of III-V Semiconductor Compounds. New York: John Wiley and Sons, 1992.
[56] E. O. Kane, The k-p Method, Semiconductors and Semimetals, vol. 1 of Physics of III-V Compounds. New York: Academic, 1966.
[57] J. M. fields,” Luttinger and W. Kohn, “Motion of electrons and holes in perturbed periodic fields,” Phys. Rev., vol. 97, 1955
[58] S. Balle, “Simple analytical approximations for the gain and refractive index spectra in quantum-well lasers,” Phys. Rev. A, vol. 57, pp. 1804-1312, Feb. 1998.
[59] T. Makino, “Analytical formulas for the optical gain of quantum wells,” IEEE J. Quantum Electron., vol. 32, pp. 493-501, Mar. 1996.
[60] M. Asada, A. Kameyama, and Y. Suematsu, “Gain and intervalence band absorption quantum-well lasers,” IEEE J. Quantum Electron., vol. 20, pp. 745-753, 1984.
[61] M. Li, M. Dion, Y. Zou, M. Davies, and S. McAlister, “An approximate k-p theory for optical gain of strain InGaAsP quantum-well lasers,” IEEE J. Quantum Electron., vol. 30, Feb. 1994.
[62] E. Zielinski, F. Keppler, S. Hausser, M. H. Pilkuhn, R. Sauer, and W. T. Tsang, “Optical gain and loss processes in GalnAs/InP MQW laser structures,” IEEE J. Quantum Electron., vol. 25, pp. 1407-2406, Dec. 1989.
[63] J. Micallef, E. H. Li, and V. L. Weiss, “Effects of interdiffusion on the sub-band- edge structure of In0.53Ga0.47As/InP single quantum wells,” J. Appl. Phys., vol. 73, pp. 7524-7532, June 1993.
注:本文由天津见合八方光电科技有限公司挑选并翻译,旨在推广和分享相关SOA基础知识,助力SOA技术的发展和应用。特此告知,本文系经过人工翻译而成,虽本公司尽最大努力保证翻译准确性,但不排除存在误差、遗漏或语义解读导致的不完全准确性,建议读者阅读原文或对照阅读,也欢迎指出错误,共同进步。
这篇关于宽光谱SOA光芯片设计(二)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







