本文主要是介绍计算机组成原理(超详解!!) 第三节 运算器(浮点加减乘),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.浮点加法、减法运算

操作过程
1.操作数检查
如果能够判断有一个操作数为0,则没必要再进行后续一系列操作,以节省运算时间。
2.完成浮点加减运算的操作
(1) 比较阶码大小并完成对阶
使二数阶码相同(即小数点位置对齐),这个过程叫作对阶。
先求两数阶码 Ex 和 Ey之差,即△E = Ex-Ey
若△E = 0,表示 Ex=Ey
若△E > 0, 表示 Ex>Ey
若△E < 0, 表示 Ex<Ey
通过尾数的移动来改变Ex或Ey,使其相等
对阶原则 : 阶码小的数向阶码大的数对齐, 小阶的尾数右移△E 位

(2) 尾数进行加或减运算
尾数求和方法与定点加减法运算完全一样。
对阶完毕可得: [x]补=00 11, 00.0011
[y]补=00 11, 11.0110
对尾数求和:

即得: [x+y]补=00 11, 11.1001
(3) 结果规格化
求和之后得到的数可能不是规格化了的数, 为了增加有效数字的位数, 提高运算精度,必须将求和的结果规格化.
①规格化的定义:
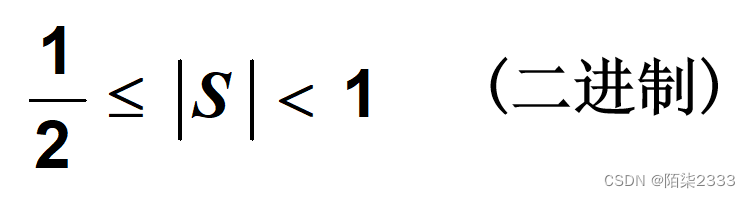
采用原码: 正数: S=0.1 ×××…× 负数: S=1.1 ×××…×
采用双符号位的补码:正数: S=00.1×××…× 负数: S=11.0×××…×

原码 :不论正数、负数,第一数位为1
补码 :符号位和第 1 数位不同
特例:

②向左规格化
若不是规格化的数,需要尾数向左移位,以实现规格化的过程,我们称其为向左规格化。
前例中, 00 11, 11.1001不是规格化数,因而需要左规,即左移一位,阶码减1
得: [x+y]补=00 10, 11.0010
③向右规格化
浮点加减运算时,尾数求和的结果也可能得到:01.×××…× 或 10.×××…×, 即两符号位不等,即结果的绝对值大于1。
此时,将尾数运算的结果右移一位,阶码加1,称为向右规格化。


(4) 舍入处理
在对阶或向右规格化时, 尾数要向右移位, 这样, 被右移的尾数的低位部分会被丢掉, 从而造成一定误差,因此要进行舍入处理。
简单的舍入方法有两种:
① “0舍1入”法:如果右移时被丢掉数位的最高位为0则舍去,反之则将尾数的末位加“1”。
② “恒置1”法:只要数位被移掉,就在尾数的末位恒置“1”。
IEEE754标准,提供的四种舍入处理方法:
就近舍入:即“四舍五入”。
朝0舍入:即朝数轴原点方向舍入
朝+ ∞舍入:正数向最低有效位进1,负数截尾
朝- ∞舍入:正数简单截尾,负数向最低有效位进1
(5)溢出处理
与定点加减法一样,浮点加减运算最后一步也需判溢出。在浮点规格化中已指出,当尾数之和(差)出现01.××…×或10.××…×时,并不表示溢出,只有将此数右规后,再根据阶码来判断浮点运算结果是否溢出。

一般说浮点溢出,均是指上溢。
浮点机的是否溢出可由阶码的符号决定:
阶码[j]补=01, ×××…× 为上溢,机器停止运算,做中断处理;
阶码[j]补=10, ×××…× 为下溢,按机器零处理。
与定点数的加减溢出的双符号位判断原则一样
fs1fs2 = 00 结果为正数,无溢出
fs1fs2 = 01 结果正溢
fs1fs2 = 10 结果负溢
fs1fs2 = 11 结果为负数,无溢出
小结
1.浮点数的溢出是以其阶码溢出表现出来的
在加、减运算过程中要检查是否产生了溢出:若阶码正常,加减运算正常结束;若阶码溢出,则要进行相应的处理。
阶码上溢—— 超过了阶码可能表示的最大值的正指数值,一般将其认为是+∞和-∞。
阶码下溢—— 超过了阶码可能表示的最小值的负指数值,一般将其认为是0。
2.对尾数的溢出也需要处理
尾数上溢:两个同符号尾数相加产生了最高位向上的进位,进行“右规”
尾数下溢:在尾数右移时,最低有效位从右端流出,要进行舍入处理


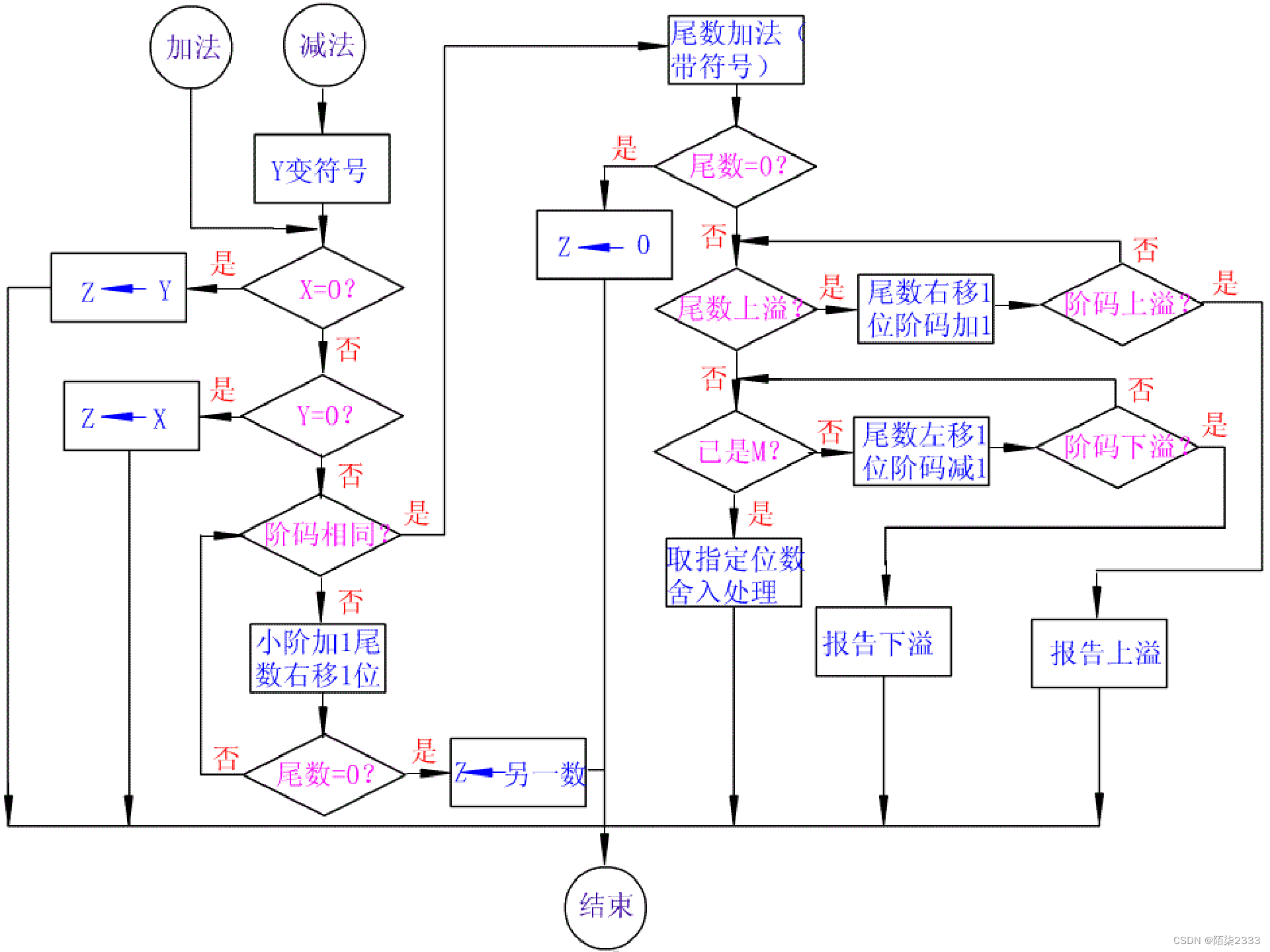
3.加减法运算器原理图
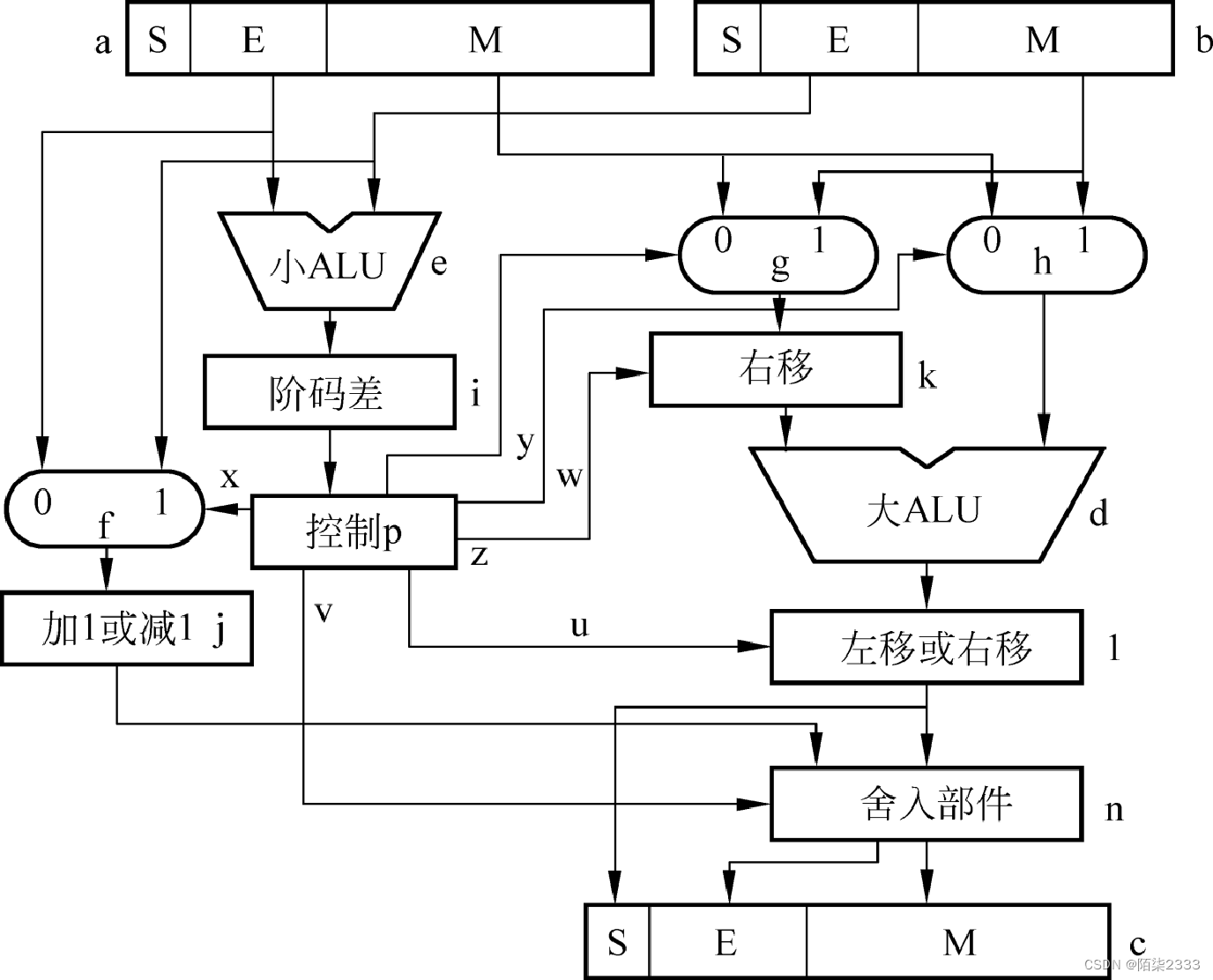
4.部件说明
a、b、c为三个浮点数据寄存器,其中a、b中存放待运算的2个浮点操作数,c中存放运算结果操作数;
d、e为2个ALU,d为大ALU,用来进行尾数运算,e为小ALU,用来进行阶码运算;
f、g、h为三个2选一的选择器;
k为尾数右移部件,用于对阶时操作;
l为左移/右移部件,用于对大ALU运算结果的规格化;
i为阶码差寄存器; j为阶码加1/减1器件,用于对阶后操作及舍入操作;
n为舍入部件,用于舍入操作;
p为操作控制器,根据阶码差控制相关部件的操作;
5.工作过程简介
(1) 对阶
a,b中的两个阶码送e(小ALU)进行对阶操作,结果存入i(阶码差寄存器),然后送p(操作控制器),根据阶码差对尾数进行移位操作。
操作控制器输出x、y、z、u、v、w,6个控制信号。信号y控制选择器g将阶码较小数的尾数送k(右移部件)。同时,对较小的阶码进行加1操作(由操作控制信号x控制),对阶后的阶码作为结果操作数的阶码。
(2) 尾数运算
经过对阶后的2个尾数送入d(大ALU)进行加减运算,运算结果送入l(左移/右移部件)进行规格化。
(3) 运算结果规格化
规格化时对运算结果的尾数进行左移或右移由操作控制器p的控制信号u控制,同时结果的阶码进行加1或减1操作,由j(加1/减1部件)实现,尾数右移,阶码加1,尾数左移,阶码减1。
(4) 舍入处理
规格化后数据送n舍入部件,经过舍入操作的数据结果送入c(结果数据寄存器)。
6.练习




2.浮点运算流水线
1、提高并行性的两个渠道
空间并行性:增加冗余部件,如增加多操作部件处理机和超标量处理机
时间并行性:改善操作流程如:流水线技术
2、流水技术原理
仿照工厂中流水装配线原理,对计算机中复杂任务进行流水线处理。首先把任务分割为一系列子任务,使各子任务能在流水线的各个阶段并发地执行,这是实现计算机时间并行性的一种方法。
假设作业T被分成k个子任务,可表达为T={T1,T2,…,Tk}
各个子任务之间具有一定的优先关系,如i<j,则处理完Ti后,才能处理Tj,这种具有线性优先关系的流水线称为线性流水线。
在流水线中必须是连续的任务,只有不断的提供任务才能充分发挥流水线的效率
把一个任务分解为几个有联系的子任务。每个子任务由一个专门的功能部件实现
在流水线中的每个功能部件之后都要有一个缓冲寄存器,或称为锁存器
流水线中各段的时间应该尽量相等,否则将会引起“堵塞”和“断流”的现象
流水线需要有装入时间和排空时间,只有当流水线完全充满时,才能充分发挥效率
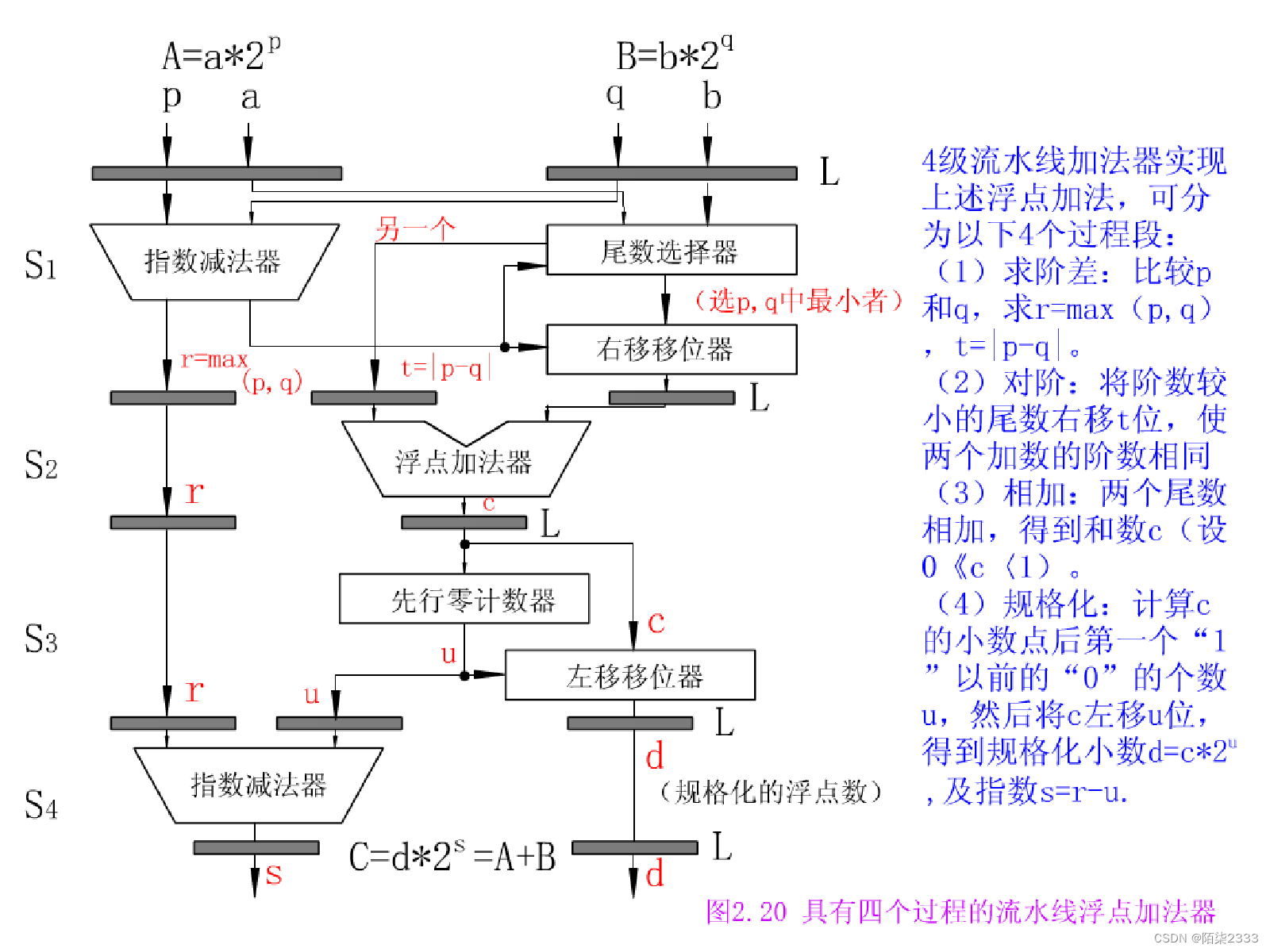
3.流水线浮点运算器
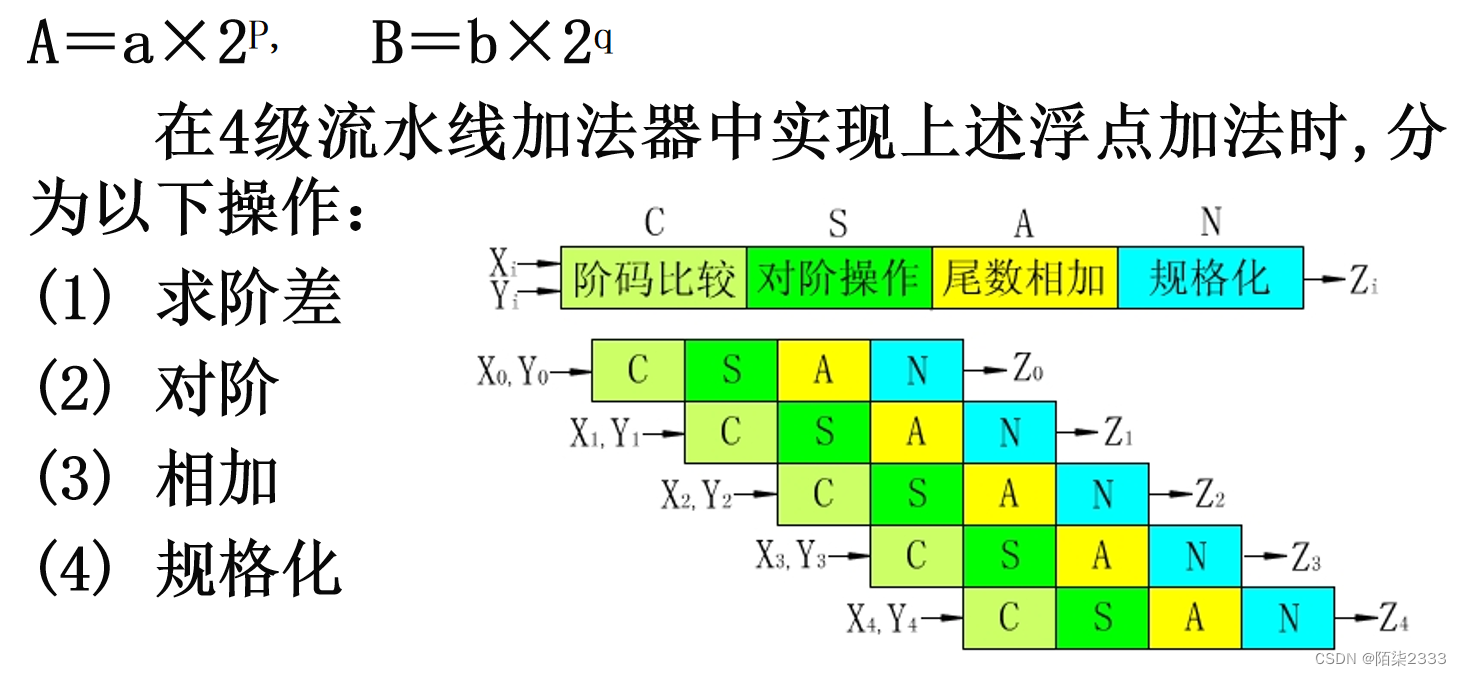
4. 流水线浮点加法器
这篇关于计算机组成原理(超详解!!) 第三节 运算器(浮点加减乘)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




